Как интерпретировать масштаб и график местоположения: с примерами

Масштабированная диаграмма местоположения — это тип диаграммы, которая отображает подобранные значения модели регрессии по оси X и квадратный корень из стандартизированных остатков по оси Y.

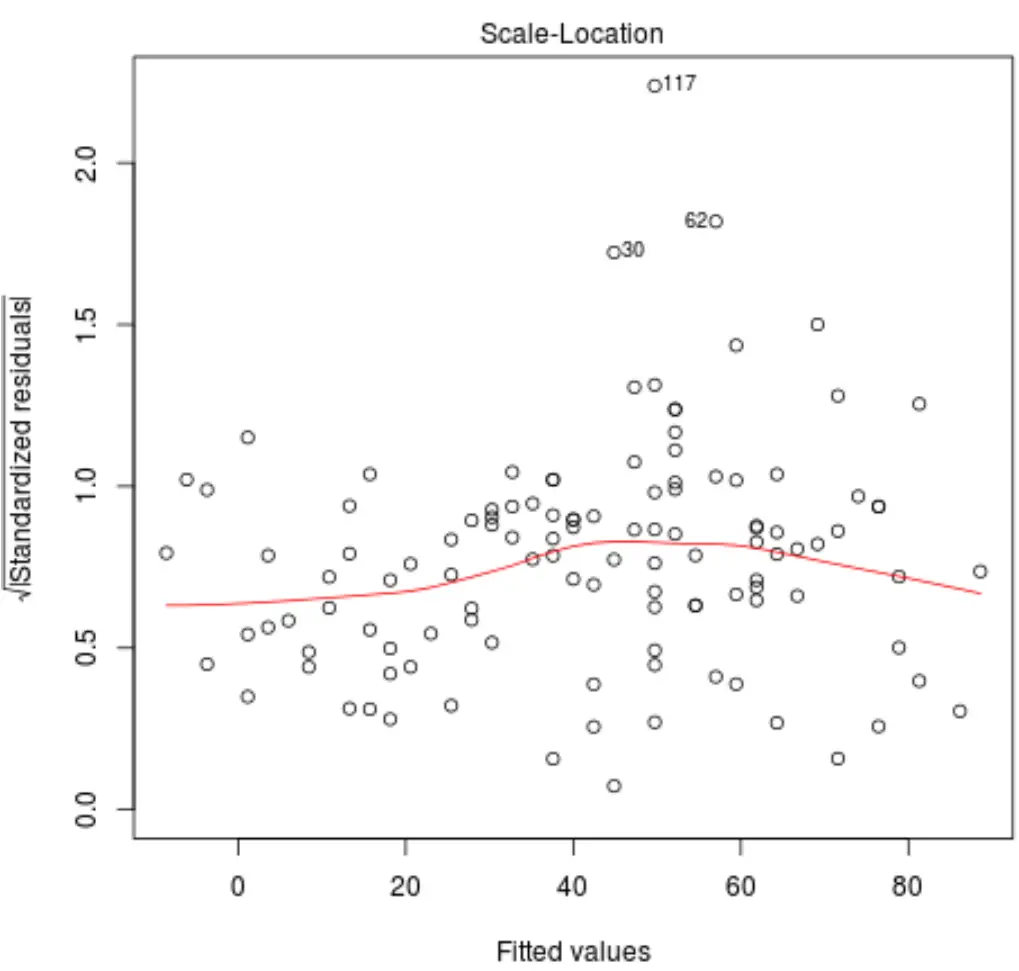
Глядя на этот график, мы проверяем две вещи:

1. Убедитесь, что красная линия на графике примерно горизонтальна. Если это так, то предположение о гомоскедастичности , вероятно, удовлетворяется для данной регрессионной модели. То есть распределение остатков примерно одинаково для всех подобранных значений.

2. Убедитесь, что среди остатков нет четкой тенденции. Другими словами, остатки должны быть случайным образом разбросаны вокруг красной линии с примерно одинаковой изменчивостью для всех подобранных значений.

Построение масштаба и местоположения в R

Мы можем использовать следующий код, чтобы подогнать простую модель линейной регрессии в R и построить график масштаба и местоположения для полученной модели:

 #fit simple linear regression model
model <- lm(Ozone ~ Temp, data = airquality)

#produce scale-location plot
plot(model)

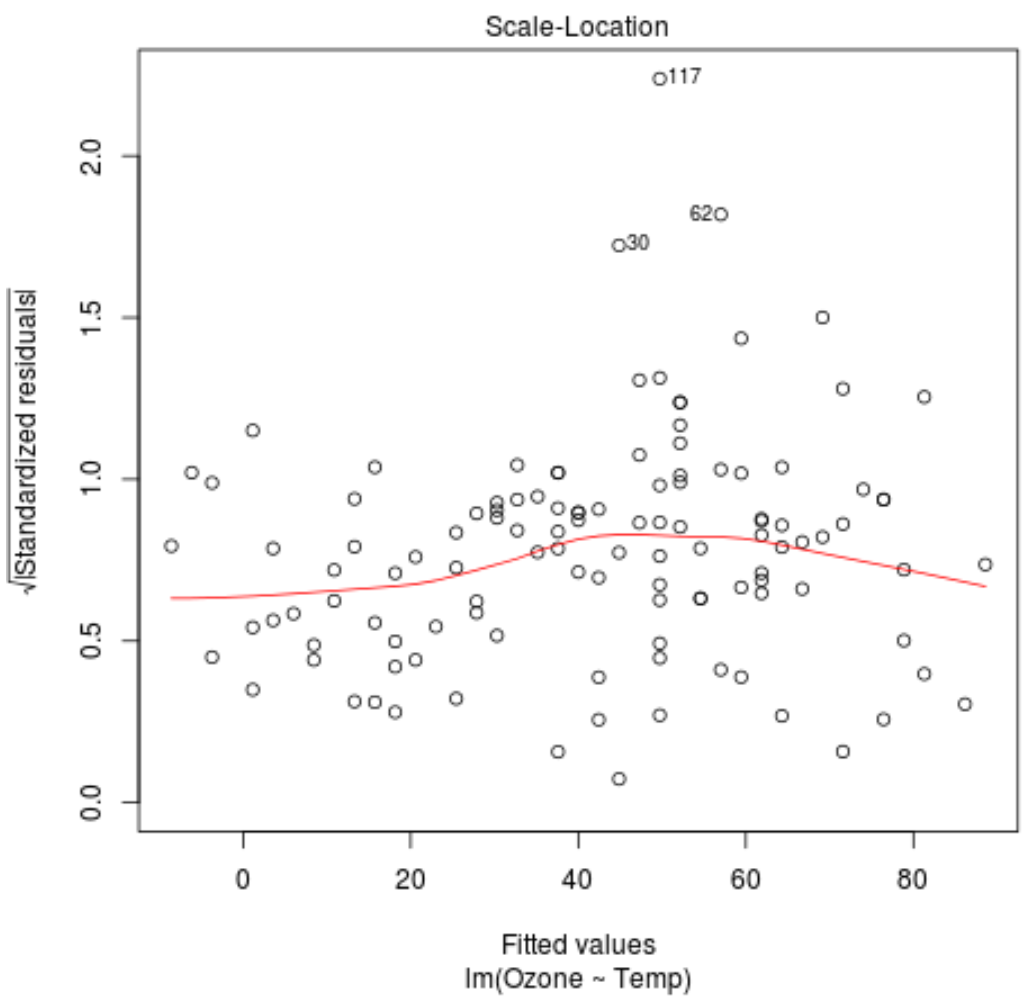
На графике масштаба и местоположения этой регрессионной модели мы можем наблюдать следующие две вещи.

1. Красная линия на графике примерно горизонтальна. Если это так, то предположение о гомоскедастичности удовлетворяется для данной регрессионной модели. То есть распределение остатков примерно одинаково для всех подобранных значений.

2. Убедитесь, что среди остатков нет четкой тенденции. Другими словами, остатки должны быть случайным образом разбросаны вокруг красной линии с примерно одинаковой изменчивостью для всех подобранных значений.

Технические примечания

Три наблюдения из набора данных с наиболее высокими стандартизированными остатками отмечены на графике.

Мы видим, что наблюдения в строках 30, 62 и 117 имеют самые высокие стандартизованные остатки.

Это не обязательно означает, что эти наблюдения являются выбросами, но вы можете взглянуть на исходные данные, чтобы более внимательно изучить эти наблюдения.

Хотя мы видим, что красная линия на графике расположения шкалы примерно горизонтальна, это служит лишь визуальным способом проверить, выполняется ли предположение о гомоскедастичности.

Формальный статистический тест, который мы можем использовать, чтобы увидеть, выполняется ли предположение о гомоскедастичности, — это тест Бреуша-Пэгана .

Тест Бреуша-Пэгана в R

Следующий код показывает, как использовать функцию bptest() пакета lmtest для выполнения теста Бреуша-Пэгана в R:

 #load lmtest package
library(lmtest)

#perform Breusch-Pagan Test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 1.4798, df = 1, p-value = 0.2238

Тест Бреуша-Пэгана использует следующие нулевые и альтернативные гипотезы:

• Нулевая гипотеза (H ₀ ): остатки гомоскедастичны (т.е. равномерно распределены).
• Альтернативная гипотеза ( _HA ): остатки гетероскедастичны (т.е. распределены неравномерно).

Из результата мы видим, что значение p теста составляет 0,2238 . Поскольку это значение p не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы утверждать, что гетероскедастичность присутствует в регрессионной модели.

Этот результат соответствует нашему визуальному осмотру красной линии на графике масштаба и местоположения.

Дополнительные ресурсы

Понимание гетероскедастичности в регрессионном анализе
Как создать остаточный график в R
Как выполнить тест Бреуша-Пэгана в R