Как использовать метод локтя в python для поиска оптимальных кластеров
Один из наиболее распространенных алгоритмов кластеризации в машинном обучении известен как кластеризация k-средних .
Кластеризация K-средних — это метод, при котором мы помещаем каждое наблюдение из набора данных в один из K- кластеров.
Конечная цель состоит в том, чтобы иметь K кластеров, в которых наблюдения внутри каждого кластера очень похожи друг на друга, в то время как наблюдения в разных кластерах сильно отличаются друг от друга.
При кластеризации k-средних первым шагом является выбор значения K — количества кластеров, в которые мы хотим поместить наблюдения.
Один из наиболее распространенных способов выбора значения K известен как метод локтя , который включает в себя создание графика с количеством кластеров по оси x и общей суммой квадратов по оси y, а затем идентифицирует где в сюжете появляется «колено» или поворот.
Точка на оси X, где находится «перелом», указывает нам оптимальное количество кластеров для использования в алгоритме кластеризации k-средних.
В следующем примере показано, как использовать метод «локоть» в Python.
Шаг 1. Импортируйте необходимые модули.
Сначала мы импортируем все модули, которые нам понадобятся для кластеризации k-средних:
import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler
Шаг 2. Создайте DataFrame
Далее мы создадим DataFrame, содержащий три переменные для 20 разных баскетболистов:
#createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
np.nan, 9, 4, 3, 4, 12, 15, 11],
' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})
#drop rows with NA values in any columns
df = df. dropna ()
#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)
Шаг 3. Используйте метод локтя, чтобы найти оптимальное количество кластеров
Допустим, мы хотим использовать кластеризацию k-средних для группировки похожих участников на основе этих трех показателей.
Чтобы выполнить кластеризацию k-средних в Python, мы можем использовать функцию KMeans из модуля sklearn .
Самый важный аргумент этой функции — n_clusters , который указывает, в скольких кластерах следует разместить наблюдения.
Чтобы определить оптимальное количество кластеров, мы создадим график, который отображает количество кластеров, а также SSE (сумму квадратов ошибок) модели.
Затем мы будем искать «колено», где сумма квадратов начинает «сгибаться» или стабилизироваться. Эта точка представляет собой оптимальное количество кластеров.
Следующий код показывает, как создать график этого типа, который отображает количество кластеров по оси X и SSE по оси Y:
#initialize kmeans parameters kmeans_kwargs = { " init ": " random ", " n_init ": 10, " random_state ": 1, } #create list to hold SSE values for each k sse = [] for k in range(1, 11): kmeans = KMeans(n_clusters=k, ** kmeans_kwargs) kmeans. fit (scaled_df) sse. append (kmeans.inertia_) #visualize results plt. plot (range(1, 11), sse) plt. xticks (range(1, 11)) plt. xlabel (" Number of Clusters ") plt. ylabel (“ SSE ”) plt. show ()
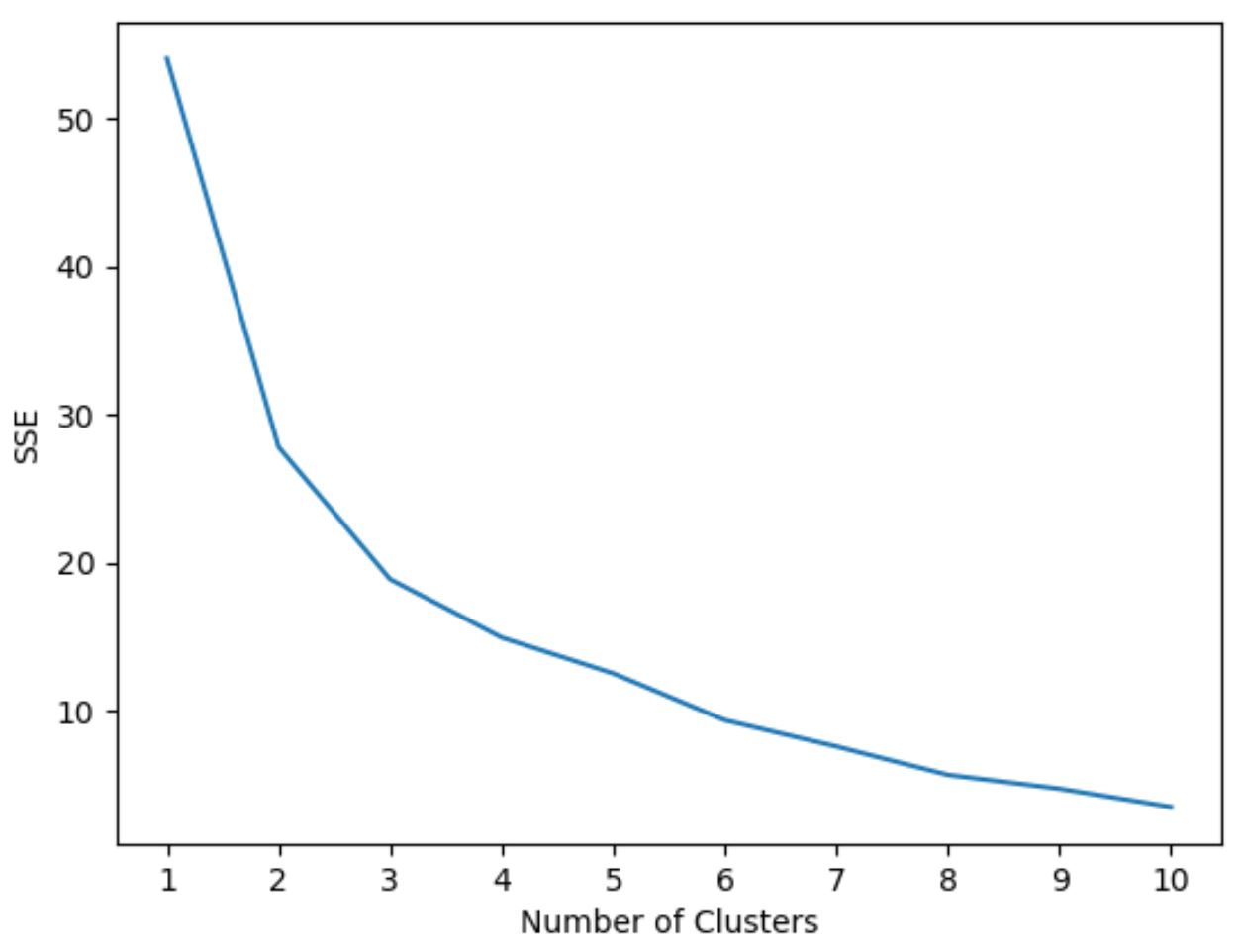
На этом графике видно, что имеется излом или «перелом» при k = 3 кластерах .
Итак, мы будем использовать 3 кластера при настройке нашей модели кластеризации k-средних на следующем этапе.
Шаг 4. Выполните кластеризацию K-средних с оптимальным K
Следующий код показывает, как выполнить кластеризацию по k-средним в наборе данных, используя оптимальное значение для k , равное 3:
#instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )
#fit k-means algorithm to data
kmeans. fit (scaled_df)
#view cluster assignments for each observation
kmeans. labels_
array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0])
В результирующей таблице показаны назначения кластеров для каждого наблюдения в DataFrame.
Чтобы облегчить интерпретацию этих результатов, мы можем добавить столбец в DataFrame, который показывает назначение кластера каждому игроку:
#append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_
#view updated DataFrame
print (df)
points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0
Столбец кластера содержит номер кластера (0, 1 или 2), которому назначен каждый игрок.
Игроки, принадлежащие к одному кластеру, имеют примерно схожие значения столбцов очков , передач и подборов .
Примечание . Полную документацию по функции KMeans sklearn можно найти здесь .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи на Python:
Как выполнить линейную регрессию в Python
Как выполнить логистическую регрессию в Python
Как выполнить перекрестную проверку K-Fold в Python