Как использовать метод elbow в r для поиска оптимальных кластеров
Один из наиболее часто используемых алгоритмов кластеризации в машинном обучении известен как кластеризация k-средних .
Кластеризация K-средних — это метод, при котором мы помещаем каждое наблюдение из набора данных в один из K- кластеров.
Конечная цель состоит в том, чтобы иметь K кластеров, в которых наблюдения внутри каждого кластера очень похожи друг на друга, в то время как наблюдения в разных кластерах сильно отличаются друг от друга.
При кластеризации k-средних первым шагом является выбор значения K — количества кластеров, в которые мы хотим поместить наблюдения.
Один из наиболее распространенных способов выбора значения K известен как метод локтя , который включает в себя создание графика с количеством кластеров по оси X и общей суммой квадратов по оси Y, а затем идентифицирует где в сюжете появляется «колено» или поворот.
Точка на оси X, где находится «перелом», указывает нам оптимальное количество кластеров для использования в алгоритме кластеризации k-средних.
В следующем примере показано, как использовать метод локтя в R.
Пример: использование метода локтя в R
В этом примере мы будем использовать набор данных USArrests , встроенный в R, который содержит количество арестов на 100 000 человек в каждом штате США в 1973 году за убийства, нападения и изнасилования, а также процент населения каждого штата, проживающего в городах. области. , Урбанпоп.
Следующий код показывает, как загрузить набор данных, удалить строки с пропущенными значениями и масштабировать каждую переменную в наборе данных, чтобы получить среднее значение 0 и стандартное отклонение 1:
#load data df <-USArrests #remove rows with missing values df <- na. omitted (df) #scale each variable to have a mean of 0 and sd of 1 df <- scale(df) #view first six rows of dataset head(df) Murder Assault UrbanPop Rape Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473 Alaska 0.50786248 1.1068225 -1.2117642 2.484202941 Arizona 0.07163341 1.4788032 0.9989801 1.042878388 Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602 California 0.27826823 1.2628144 1.7589234 2.067820292 Colorado 0.02571456 0.3988593 0.8608085 1.864967207
Чтобы найти оптимальное количество кластеров для использования в алгоритме k-средних, мы будем использовать функцию fviz_nbclust() из пакета factoextra , чтобы создать график зависимости количества кластеров от общего числа в сумме квадратов:
library (cluster) library (factoextra) #create plot of number of clusters vs total within sum of squares fviz_nbclust(df, kmeans, method = “ wss ”)
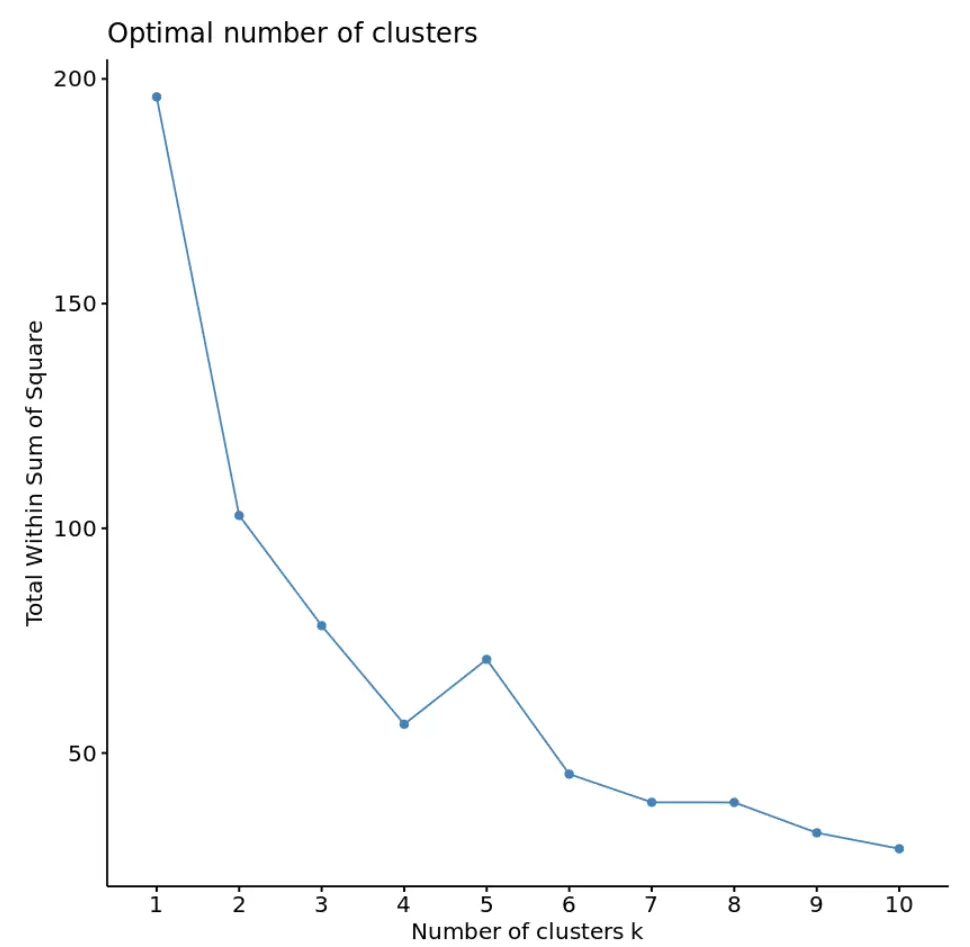
На этом графике видно, что в кластерах k = 4 имеется «перегиб» или излом. Это момент, когда сумма квадратов начинает стабилизироваться.
Это говорит нам о том, что оптимальное количество кластеров для использования в алгоритме k-средних равно 4.
Примечание . Хотя мы могли бы получить меньшую сумму квадратов, используя больше кластеров, мы , скорее всего, переопределим обучающие данные , и поэтому алгоритм k-средних не будет работать так же хорошо с тестовыми данными.
Мы можем использовать функцию kmeans() из пакета кластеров для выполнения кластеризации по k-средним в наборе данных, используя оптимальное значение для k из 4:
#make this example reproducible set. seeds (1) #perform k-means clustering with k = 4 clusters km <- kmeans(df, centers = 4, nstart = 25) #view results km K-means clustering with 4 clusters of sizes 16, 13, 13, 8 Cluster means: Murder Assault UrbanPop Rape 1 -0.4894375 -0.3826001 0.5758298 -0.26165379 2 -0.9615407 -1.1066010 -0.9301069 -0.96676331 3 0.6950701 1.0394414 0.7226370 1.27693964 4 1.4118898 0.8743346 -0.8145211 0.01927104 Vector clustering: Alabama Alaska Arizona Arkansas California Colorado 4 3 3 4 3 3 Connecticut Delaware Florida Georgia Hawaii Idaho 1 1 3 4 1 2 Illinois Indiana Iowa Kansas Kentucky Louisiana 3 1 2 1 2 4 Maine Maryland Massachusetts Michigan Minnesota Mississippi 2 3 1 3 2 4 Missouri Montana Nebraska Nevada New Hampshire New Jersey 3 2 2 3 2 1 New Mexico New York North Carolina North Dakota Ohio Oklahoma 3 3 4 2 1 1 Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 1 1 1 4 2 4 Texas Utah Vermont Virginia Washington West Virginia 3 1 2 1 1 2 Wisconsin Wyoming 2 1 Within cluster sum of squares by cluster: [1] 16.212213 11.952463 19.922437 8.316061 (between_SS / total_SS = 71.2%) Available components: [1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" [7] "size" "iter" "ifault"
По результатам мы видим, что:
- В первый кластер вошли 16 штатов.
- Во второй кластер вошли 13 штатов.
- В третий кластер отнесены 13 штатов.
- 8 штатов отнесены к четвертому кластеру
Мы также можем добавить назначения кластеров каждого состояния в исходный набор данных:
#add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)
#view final data
head(final_data)
Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2
Каждое наблюдение из исходной базы данных было помещено в одну из четырех групп.
Дополнительные ресурсы
В следующих руководствах представлены пошаговые примеры запуска различных алгоритмов кластеризации в R:
Кластеризация K-средних в R: пошаговый пример
Кластеризация K-медоидов в R: пошаговый пример
Иерархическая кластеризация в R: пошаговый пример