Как использовать метод наименьших квадратов в r
Метод наименьших квадратов — это метод, который мы можем использовать для поиска линии регрессии, которая лучше всего соответствует заданному набору данных.
Чтобы использовать метод наименьших квадратов для подбора линии регрессии в R, мы можем использовать функцию lm() .
Эта функция использует следующий базовый синтаксис:
model <- lm(response ~ predictor, data=df)
В следующем примере показано, как использовать эту функцию в R.
Пример: метод наименьших квадратов в R
Предположим, у нас есть следующий фрейм данных в R, который показывает количество изученных часов и соответствующий балл на экзамене для 15 учеников в классе:
#create data frame df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14), score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89)) #view first six rows of data frame head(df) hours score 1 1 64 2 2 66 3 4 76 4 5 73 5 5 74 6 6 81
Мы можем использовать функцию lm() , чтобы использовать метод наименьших квадратов и подогнать линию регрессии к этим данным:
#use method of least squares to fit regression line model <- lm(score ~ hours, data=df) #view regression model summary summary(model) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -5,140 -3,219 -1,193 2,816 5,772 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 65,334 2,106 31,023 1.41e-13 *** hours 1.982 0.248 7.995 2.25e-06 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.641 on 13 degrees of freedom Multiple R-squared: 0.831, Adjusted R-squared: 0.818 F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06
Из значений в столбце «Оценочный результат» мы можем написать следующую подобранную линию регрессии:
Оценка за экзамен = 65,334 + 1,982 (часы)
Вот как интерпретировать каждый коэффициент в модели:
- Перехват : для студента, который учится 0 часов, ожидаемый результат экзамена составляет 65,334 .
- часов : за каждый дополнительный учебный час ожидаемый балл на экзамене увеличивается на 1982 .
Мы можем использовать это уравнение, чтобы оценить оценку за экзамен, которую получит студент, исходя из количества учебных часов.
Например, если студент учится 5 часов, мы предполагаем, что его балл на экзамене составит 75,244:
Оценка на экзамене = 65,334 + 1,982(5) = 75,244
Наконец, мы можем создать диаграмму рассеяния исходных данных с наложенной на график подобранной линией регрессии:
#create scatter plot of data plot(df$hours, df$score, pch=16, col=' steelblue ') #add fitted regression line to scatter plot abline(model)
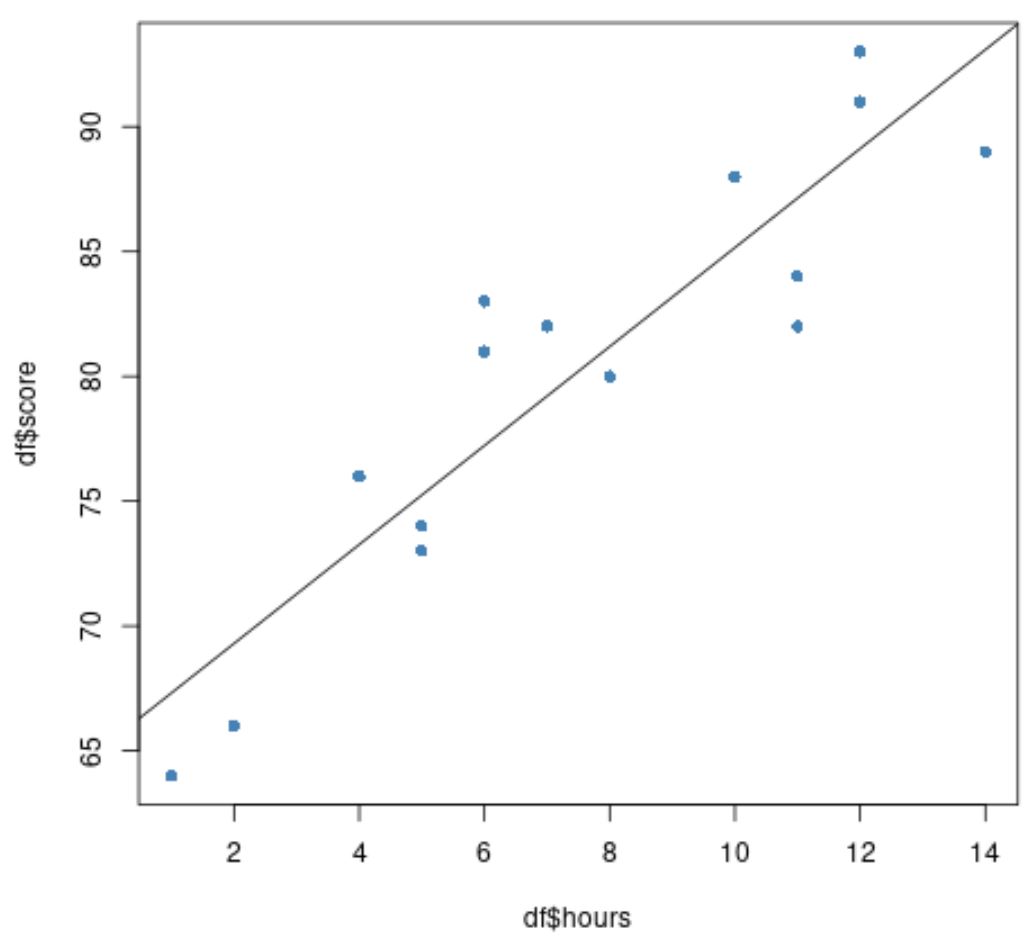
Синие круги представляют данные, а черная линия представляет собой подобранную линию регрессии.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:
Как создать остаточный график в R
Как проверить мультиколлинеарность в R
Как выполнить подгонку кривой в R