Как выполнить множественную линейную регрессию в excel
Множественная линейная регрессия — это метод, который мы можем использовать, чтобы понять взаимосвязь между двумя или более объясняющими переменными и переменной отклика .
В этом руководстве объясняется, как выполнить множественную линейную регрессию в Excel.
Примечание. Если у вас есть только одна объясняющая переменная, вместо этого вам следует выполнить простую линейную регрессию .
Пример: множественная линейная регрессия в Excel
Предположим, мы хотим знать, влияет ли количество часов, потраченных на обучение, и количество сданных подготовительных экзаменов на оценку, которую студент получает на определенном вступительном экзамене в колледж.
Чтобы изучить эту взаимосвязь, мы можем выполнить множественную линейную регрессию, используя часы обучения и подготовительные экзамены в качестве объясняющих переменных, а результаты экзаменов — в качестве переменной ответа.
Выполните следующие шаги в Excel, чтобы выполнить множественную линейную регрессию.
Шаг 1: Введите данные.
Введите следующие данные о количестве учебных часов, сданных подготовительных экзаменов и полученных результатах экзаменов для 20 студентов:
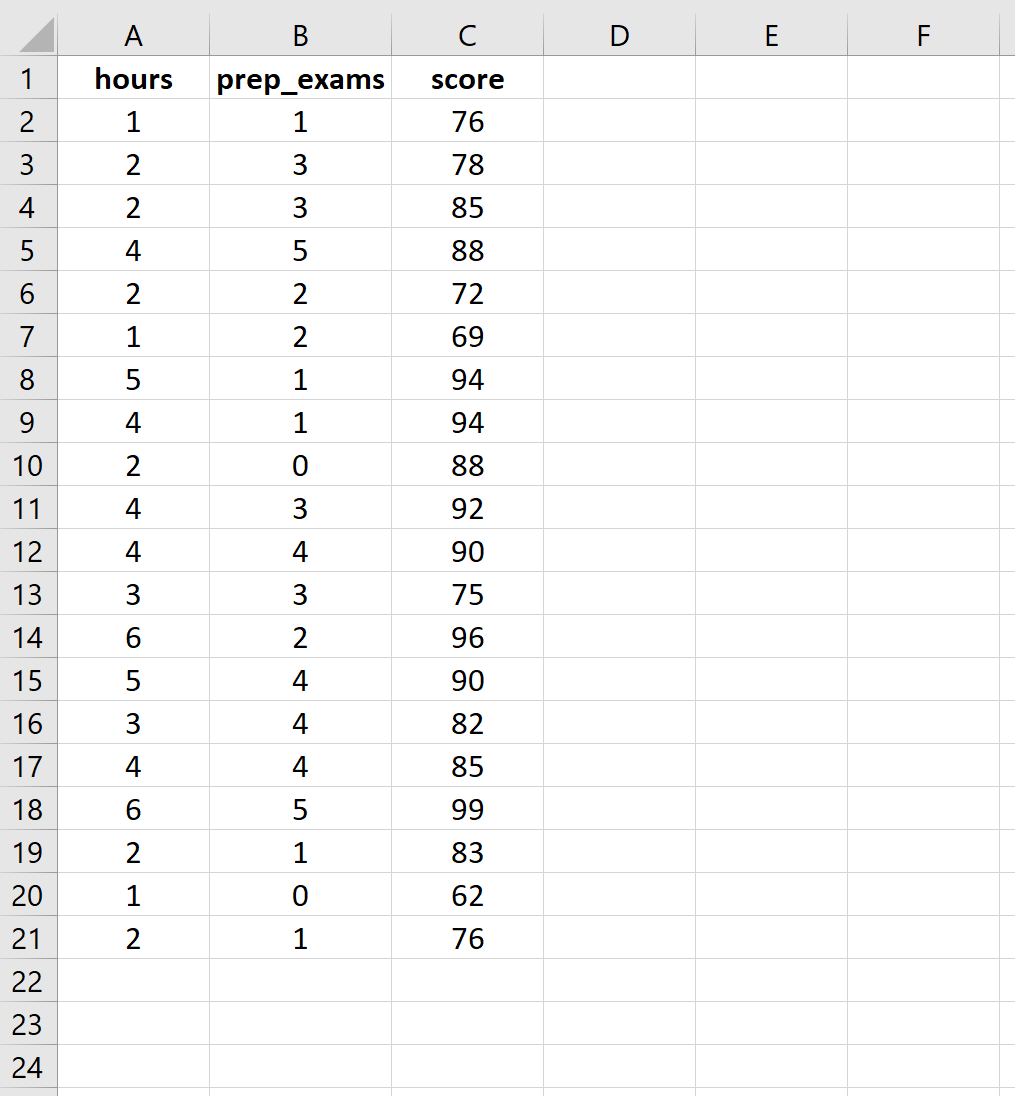
Шаг 2. Выполните множественную линейную регрессию.
На верхней ленте Excel перейдите на вкладку «Данные» и нажмите «Анализ данных» . Если вы не видите эту опцию, вам необходимо сначала установить бесплатное программное обеспечение Analysis ToolPak .

После того, как вы нажмете «Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».
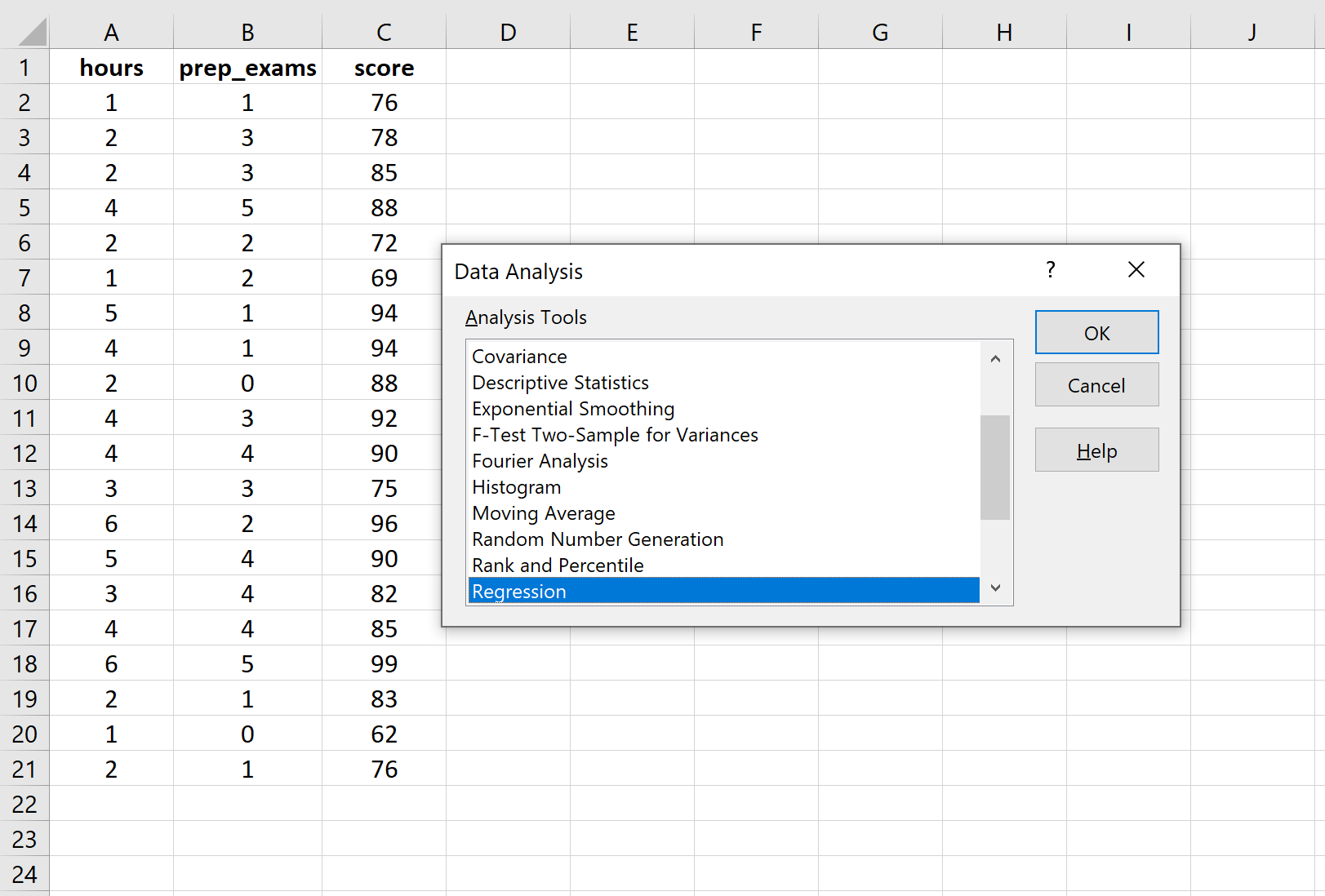
В поле «Входной диапазон Y» заполните массив значений переменной ответа. Для входного диапазона X заполните массив значений для двух независимых переменных. Установите флажок рядом с надписью «Метки» , чтобы сообщить Excel, что мы включили имена переменных во входные диапазоны. В поле Выходной диапазон выберите ячейку, в которой вы хотите, чтобы отображались выходные данные регрессии. Затем нажмите ОК .
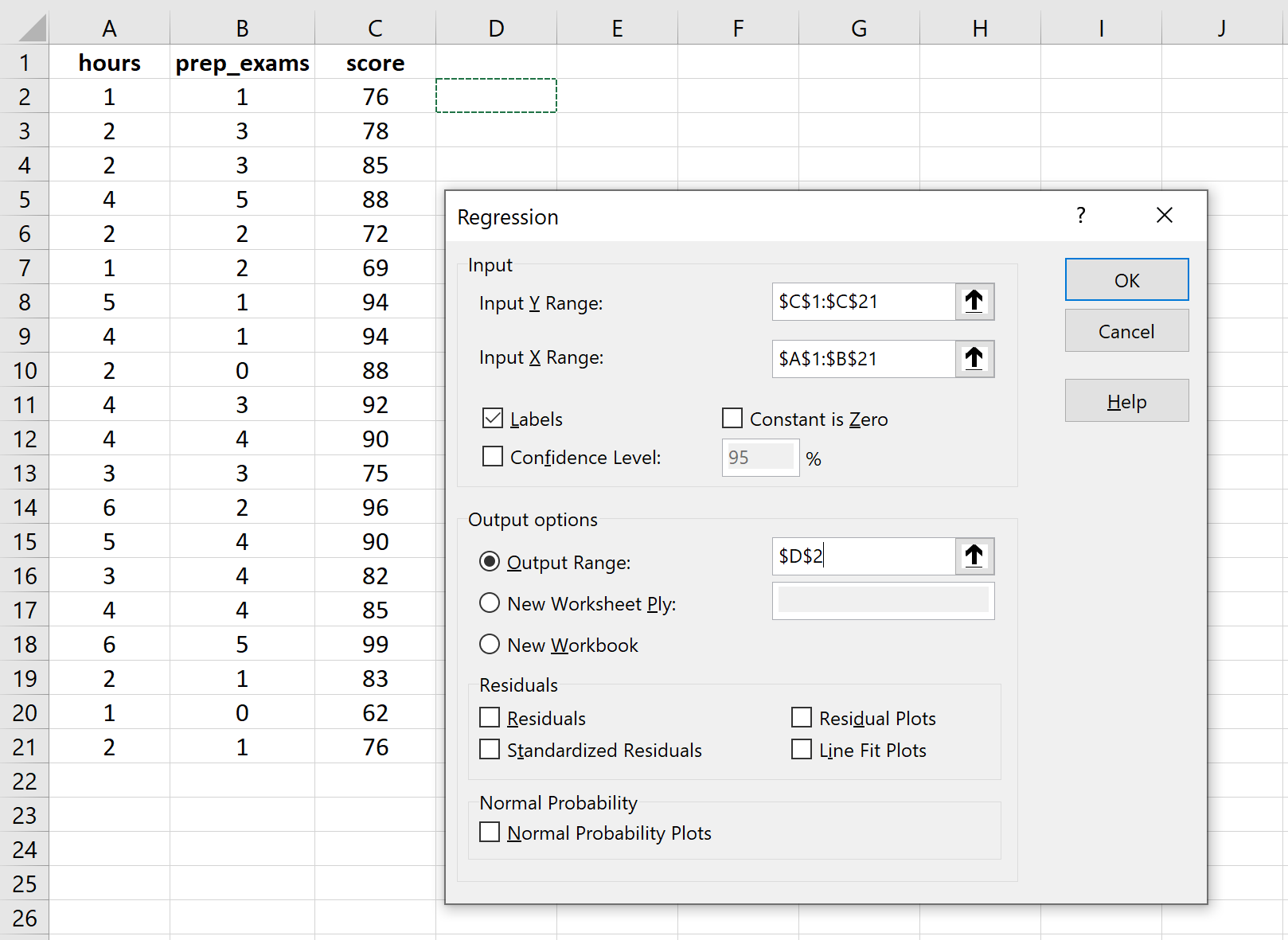
Автоматически появится следующий вывод:

Шаг 3: Интерпретируйте результат.
Вот как интерпретировать наиболее релевантные числа в результате:
R Квадрат: 0,734 . Это называется коэффициентом детерминации. Это доля дисперсии переменной отклика, которую можно объяснить объясняющими переменными. В этом примере 73,4% разницы в экзаменационных баллах объясняется количеством учебных часов и количеством сданных подготовительных экзаменов.
Стандартная ошибка: 5.366 . Это среднее расстояние между наблюдаемыми значениями и линией регрессии. В данном примере наблюдаемые значения отклоняются в среднем на 5366 единиц от линии регрессии.
F: 23:46 Это общая статистика F для регрессионной модели, рассчитанная как регрессионное MS/остаточное MS.
Значение F: 0,0000 . Это значение p, связанное с общей статистикой F. Это говорит нам, является ли регрессионная модель в целом статистически значимой или нет. Другими словами, он говорит нам, имеют ли две объединенные объясняющие переменные статистически значимую связь с переменной ответа. В этом случае значение p меньше 0,05, что указывает на то, что объясняющие переменные , часы обучения и сданные подготовительные экзамены вместе взятые имеют статистически значимую связь с результатом экзамена .
P-значения. Отдельные значения p говорят нам, является ли каждая объясняющая переменная статистически значимой или нет. Мы видим, что количество учебных часов является статистически значимым (p = 0,00), в то время как сданные подготовительные экзамены (p = 0,52) не являются статистически значимыми при α = 0,05. Поскольку прошлые подготовительные экзамены не являются статистически значимыми, мы можем в конечном итоге принять решение удалить их из модели.
Коэффициенты: Коэффициенты каждой объясняющей переменной говорят нам об ожидаемом среднем изменении переменной отклика, при условии, что другая объясняющая переменная остается постоянной. Например, ожидается, что за каждый дополнительный час, потраченный на учебу, средний балл на экзамене увеличится на 5,56 , при условии, что сдаваемые практические экзамены останутся постоянными.
Вот еще один способ взглянуть на это: если Студент А и Студент Б сдают одинаковое количество подготовительных экзаменов, но Студент А учится на час дольше, то Студент А должен набрать на 5,56 балла больше, чем студент Б.
Мы интерпретируем коэффициент пересечения как означающий, что ожидаемый результат экзамена для студента, который не учится и не сдает подготовительные экзамены, составляет 67,67 .
Расчетное уравнение регрессии: мы можем использовать коэффициенты из выходных данных модели, чтобы создать следующее расчетное уравнение регрессии:
Экзаменационный балл = 67,67 + 5,56*(часы) – 0,60*(подготовительные экзамены)
Мы можем использовать это расчетное уравнение регрессии для расчета ожидаемого результата экзамена для студента на основе количества учебных часов и количества практических экзаменов, которые он сдает. Например, студент, который учится три часа и сдает подготовительный экзамен, должен получить оценку 83,75 :
Оценка экзамена = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Имейте в виду, что, поскольку прошлые подготовительные экзамены не были статистически значимыми (p=0,52), мы можем принять решение удалить их, поскольку они не улучшают общую модель. В этом случае мы могли бы выполнить простую линейную регрессию, используя только изученные часы в качестве объясняющей переменной.
Результаты этого простого линейного регрессионного анализа можно найти здесь .
Дополнительные ресурсы
После выполнения множественной линейной регрессии вы можете проверить несколько предположений, в том числе:
1. Тестирование на мультиколлинеарность с помощью VIF .
2. Проверка гетероскедастичности с помощью теста Бреуша-Пэгана .