Множественная линейная регрессия вручную (шаг за шагом)
Множественная линейная регрессия — это метод, который мы можем использовать для количественной оценки взаимосвязи между двумя или более переменными-предикторами и переменной отклика .
В этом руководстве объясняется, как вручную выполнить множественную линейную регрессию.
Пример: множественная линейная регрессия вручную
Предположим, у нас есть следующий набор данных с переменной ответа y и двумя переменными-предикторами x 1 и x 2 :
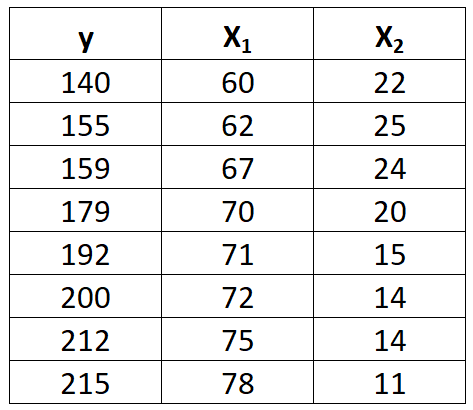
Выполните следующие шаги, чтобы подогнать модель множественной линейной регрессии к этому набору данных.
Шаг 1: Рассчитайте x 1 2 , x 2 2 , x 1 y, x 2 y и x 1 x 2 .
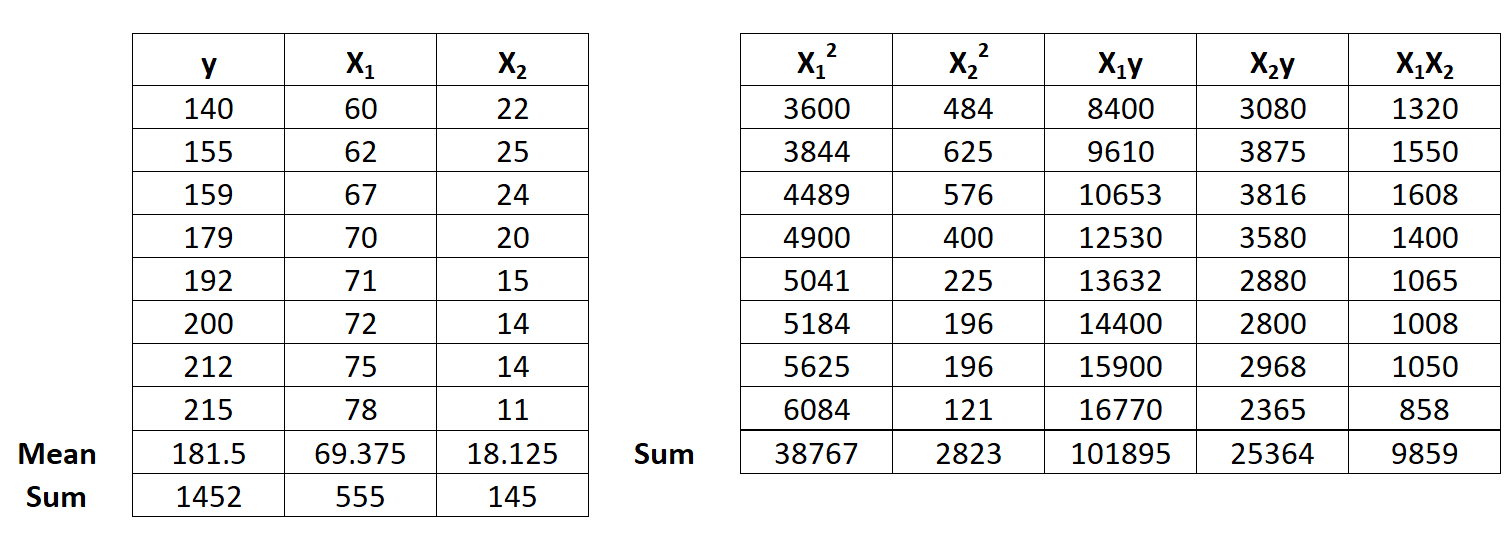
Шаг 2: Рассчитайте суммы регрессии.
Затем выполните следующие вычисления суммы регрессии:
- Σx12 = ΣX12 – ( ΣX1 ) 2 /n = 38,767 – (555) 2/8 = 263,875
- Σx22 = ΣX22 – ( ΣX2 ) 2 /n = 2823 – (145) 2/8 = 194,875
- Σ x 1 y = Σ
- Σ x 2 y = Σ
- Σ х 1 х 2 = Σ
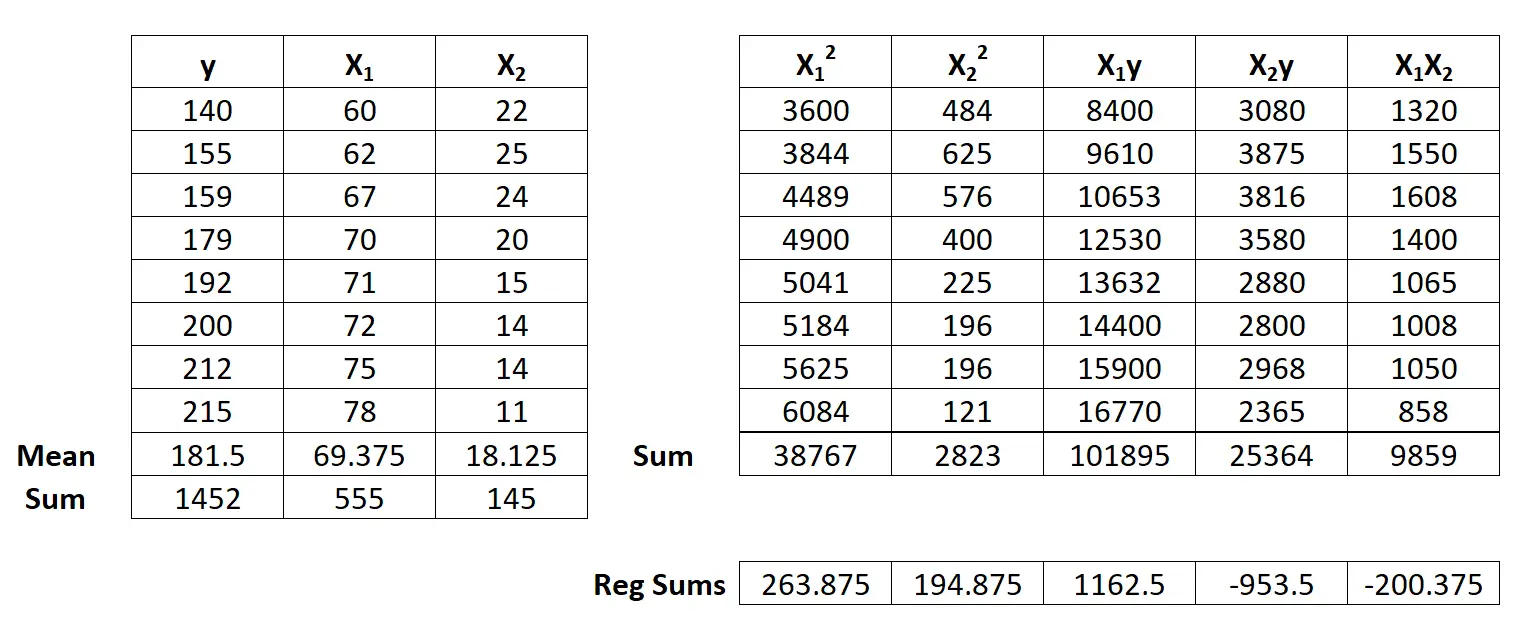
Шаг 3: Рассчитайте b 0 , b 1 и b 2 .
Формула для расчета b 1 : [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Итак, b 1 = [(194,875)(1162,5) – (-200,375)(-953,5)] / [(263,875) (194,875) – (-200,375) 2 ] = 3,148
Формула для расчета b 2 следующая: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Итак, b 2 = [(263,875)(-953,5) – (-200,375)(1152,5)] / [(263,875) (194,875) – (-200,375) 2 ] = -1,656
Формула для расчета b 0 : y – b 1 X 1 – b 2 X 2.
Таким образом, b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867.
Шаг 5: Поместите b 0 , b 1 и b 2 в предполагаемое уравнение линейной регрессии.
Предполагаемое уравнение линейной регрессии: ŷ = b 0 + b 1 *x 1 + b 2 *x 2.
В нашем примере это ŷ = -6,867 + 3,148x 1 – 1,656x 2.
Как интерпретировать уравнение множественной линейной регрессии
Вот как интерпретировать это расчетное уравнение линейной регрессии: ŷ = -6,867 + 3,148x 1 – 1,656x 2
b0 = -6,867 . Когда обе переменные-предикторы равны нулю, среднее значение y составляет -6,867.
б1 = 3,148 . Увеличение x 1 на одну единицу связано с увеличением y в среднем на 3,148 единицы, если предположить, что x 2 остается постоянным.
b2 = -1,656 . Увеличение x 2 на одну единицу связано с уменьшением y в среднем на 1656 единиц, при условии, что x 1 остается постоянным.
Дополнительные ресурсы
Введение в множественную линейную регрессию
Как выполнить простую линейную регрессию вручную
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше