Что такое монотонные отношения? (определение + примеры)
В статистике монотонная связь между двумя переменными относится к сценарию, в котором изменение одной переменной обычно связано с изменением в определенном направлении другой переменной.
Различают два типа монотонных отношений:
Положительная монотонность: когда значение одной переменной увеличивается, значение другой переменной также имеет тенденцию к увеличению.
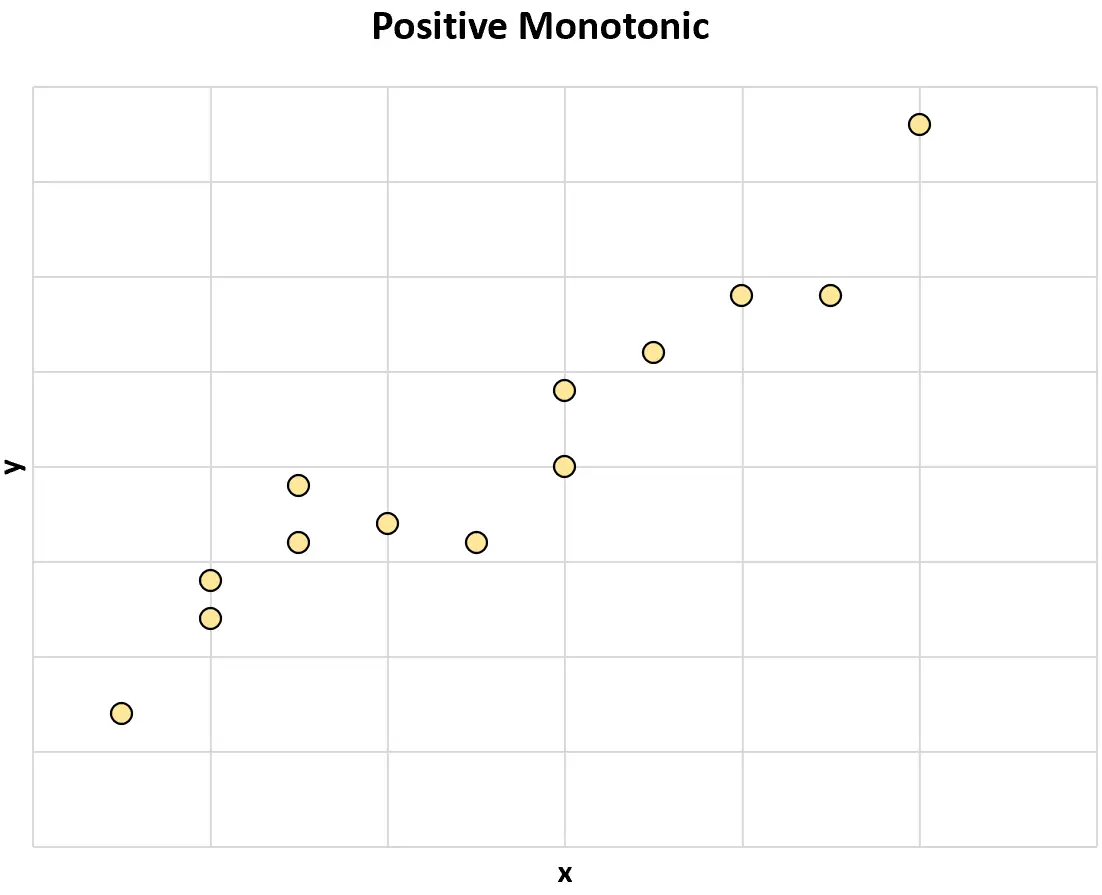
Отрицательная монотонность: когда значение одной переменной увеличивается, значение другой переменной имеет тенденцию к уменьшению.
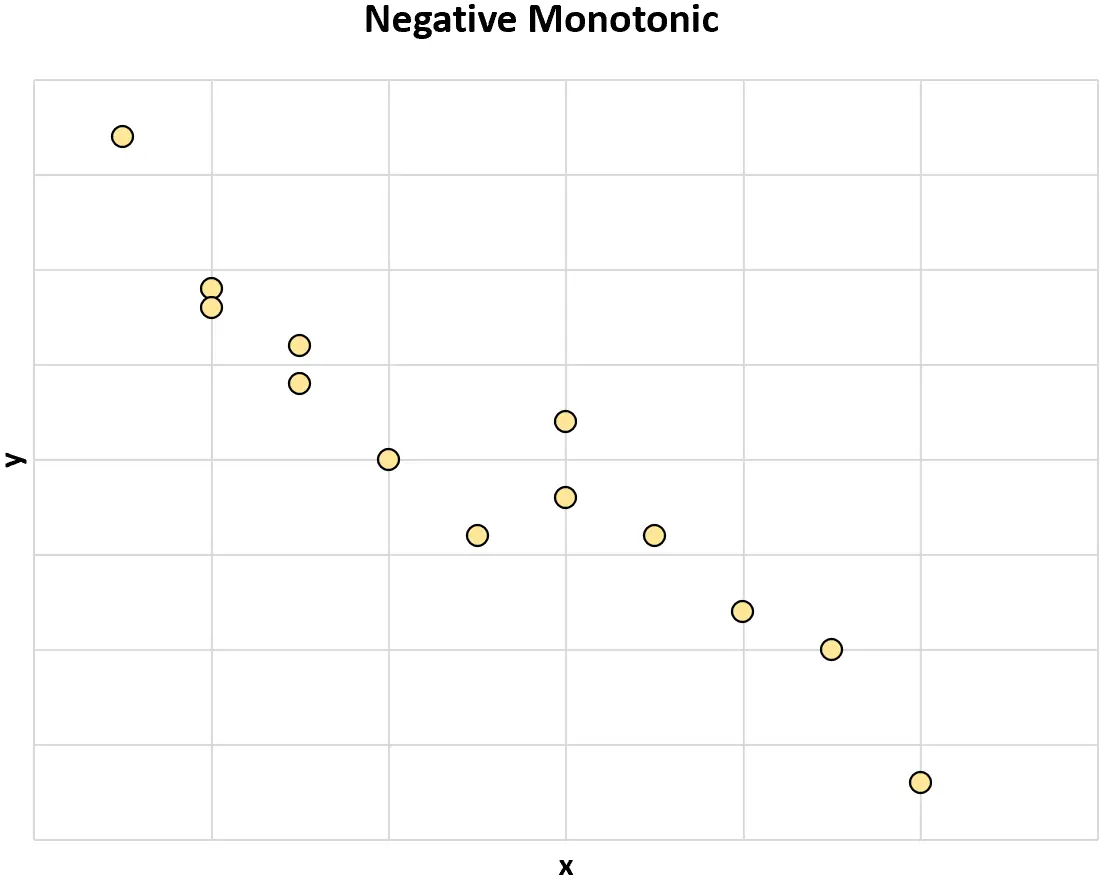
Если две переменные обычно не изменяются в одном направлении, то говорят, что они имеют немонотонную связь .
Вот пример немонотонной связи между двумя переменными:
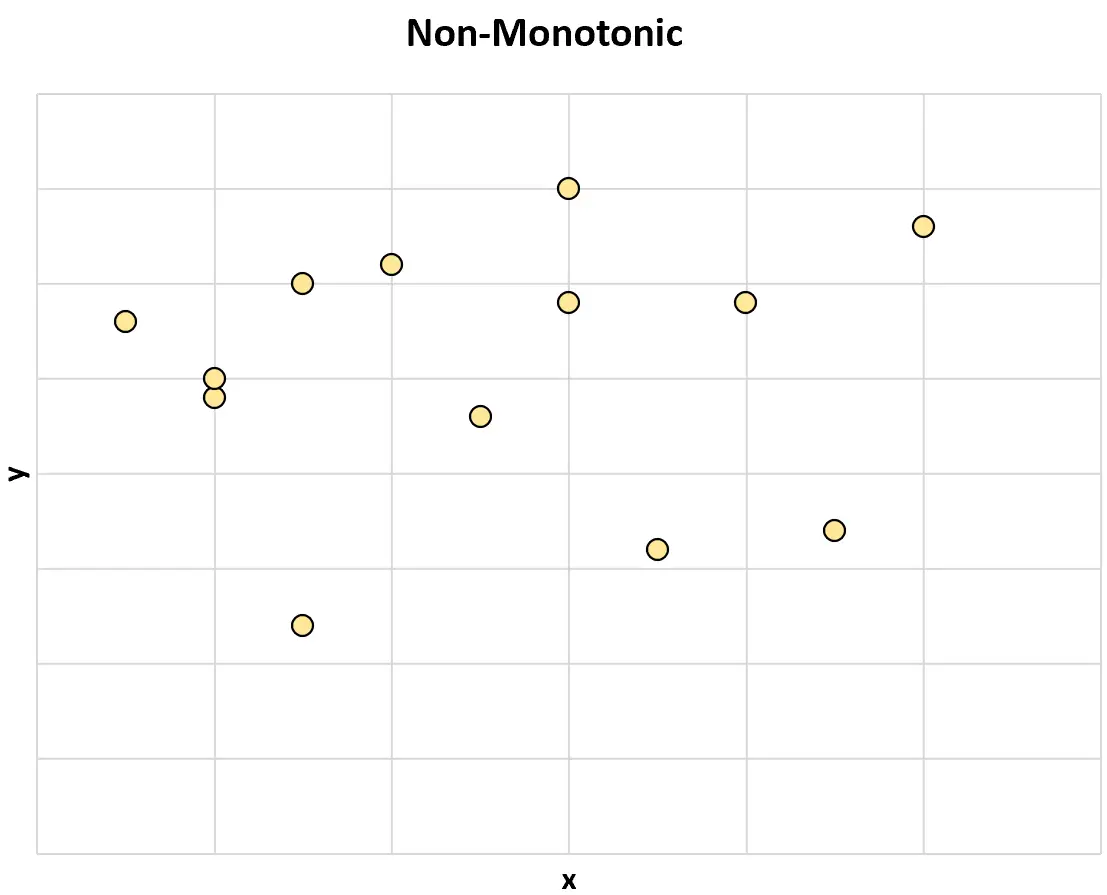
А вот еще один пример немонотонной связи между двумя переменными:
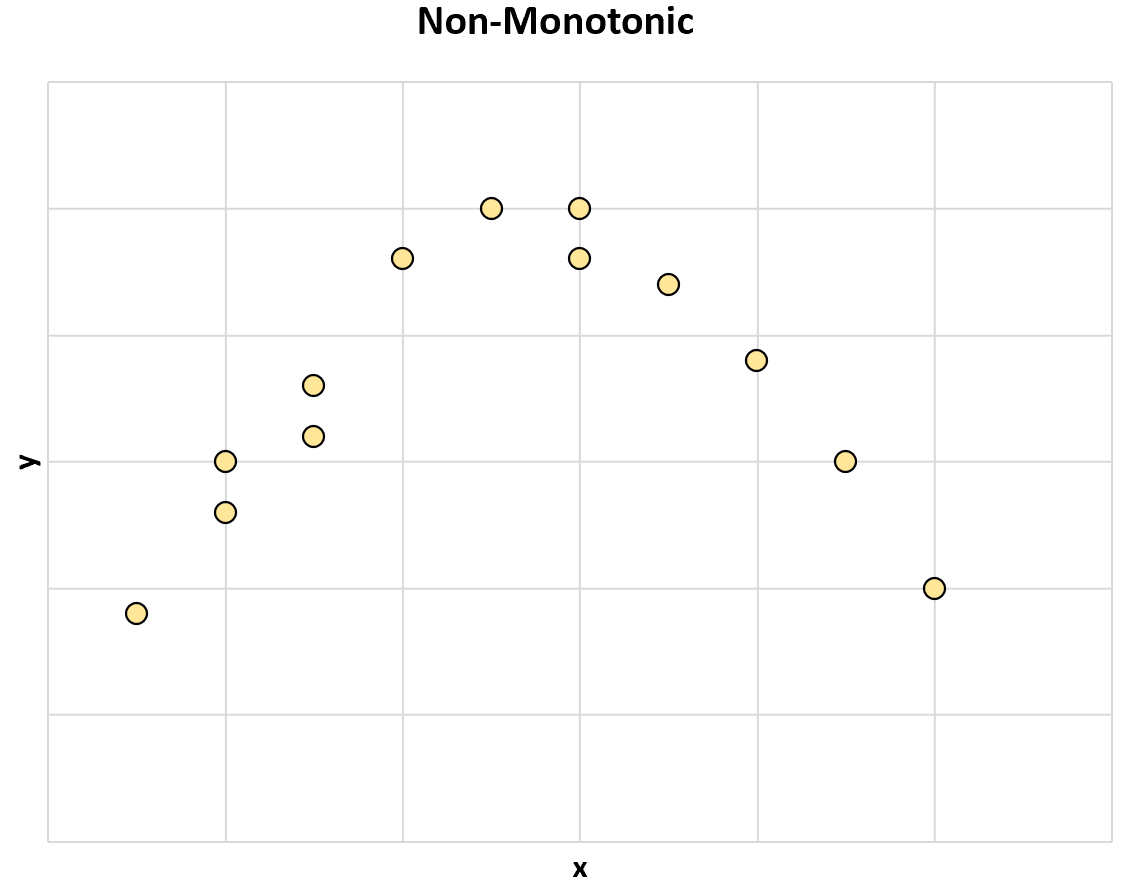
По мере увеличения значения x значение y иногда увеличивается, но иногда значение y уменьшается .
Строго монотонно или не строго монотонно.
Говорят, что две переменные имеют строго монотонную связь, если изменения одной переменной всегда связаны с изменением в том же направлении другой переменной.
Например, следующий график иллюстрирует строго положительную монотонную связь между двумя переменными:
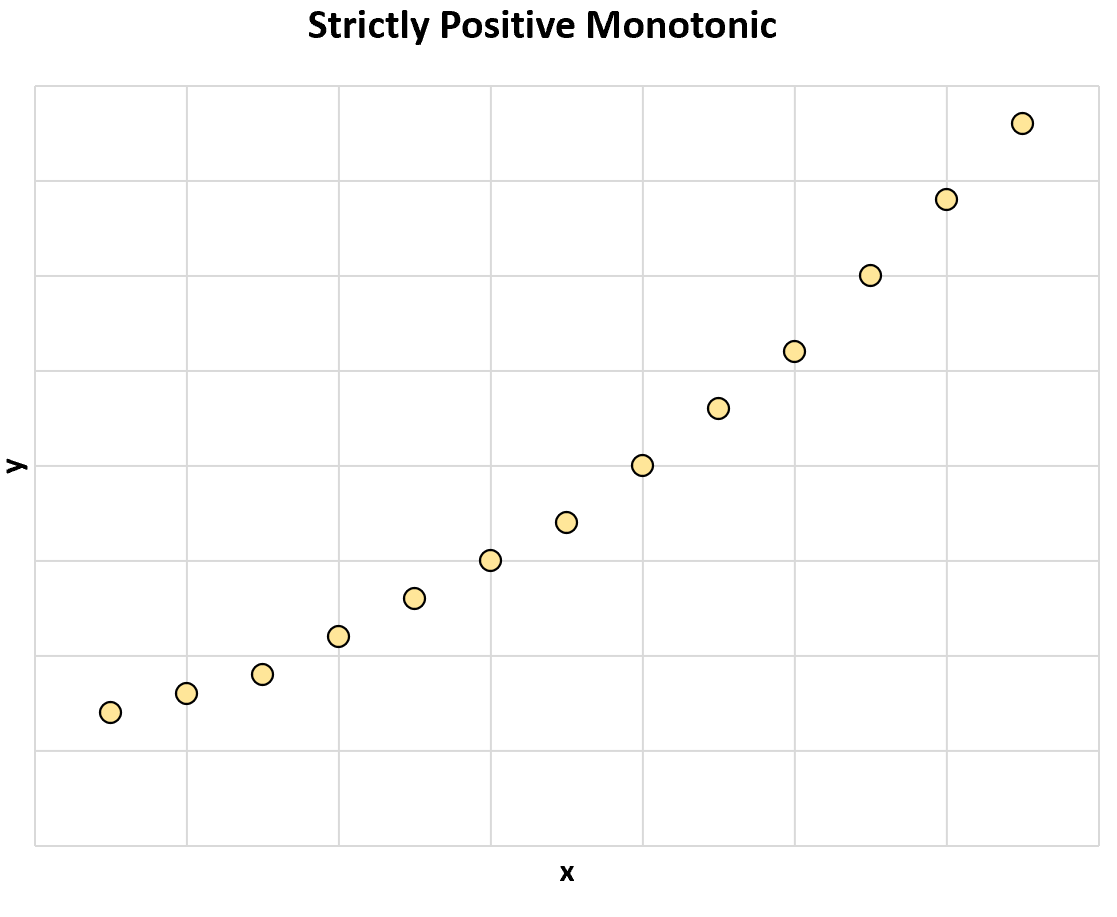
По мере увеличения значения x значение y всегда увеличивается.
Следующий график иллюстрирует строго отрицательную монотонную связь между двумя переменными:
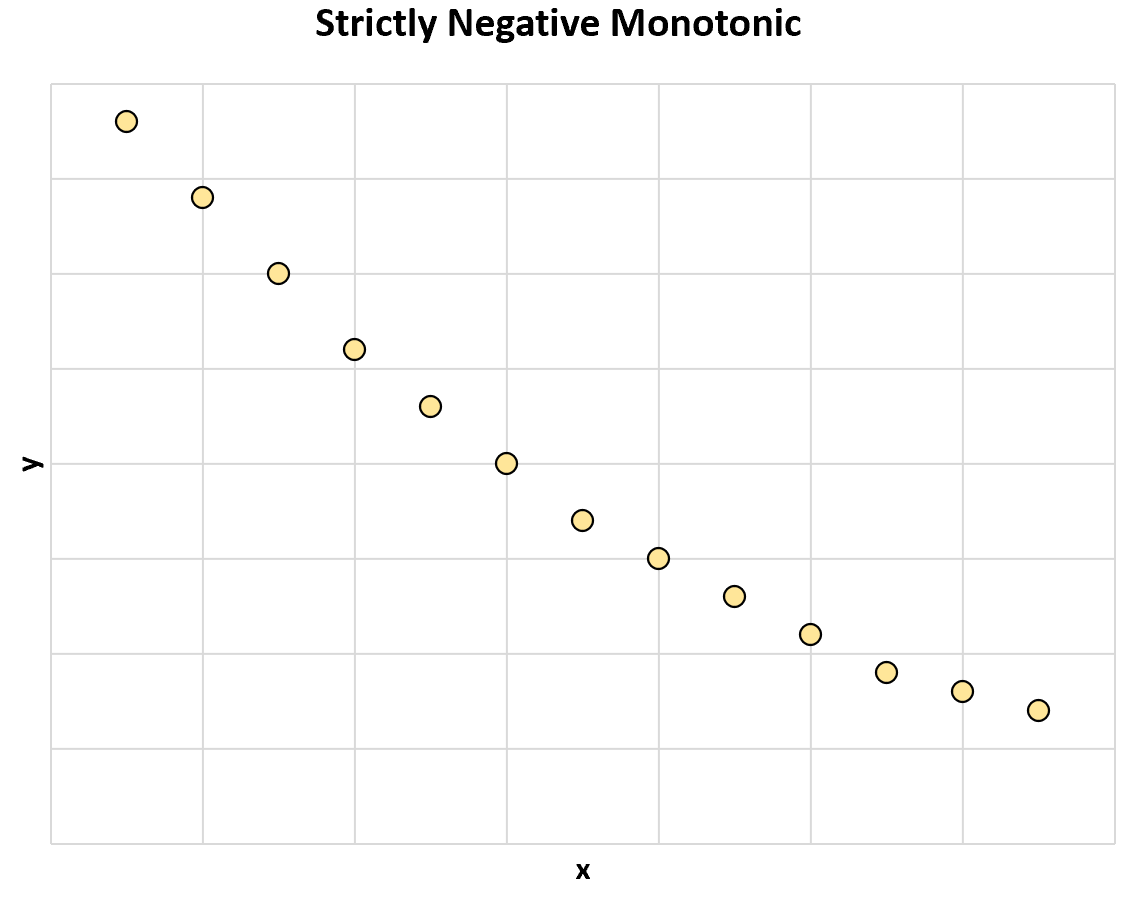
По мере увеличения значения x значение y всегда уменьшается.
Как количественно оценить монотонные отношения
Самый распространенный способ количественной оценки связи между двумя переменными — использование коэффициента корреляции Пирсона , который измеряет линейную связь между двумя переменными.
Этот коэффициент всегда принимает значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
- 0 указывает на отсутствие линейной корреляции между двумя переменными.
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чем ближе коэффициент к 1, тем сильнее положительная связь между двумя переменными. И наоборот, чем ближе коэффициент к -1, тем сильнее отрицательная связь между двумя переменными.
Однако если связь между двумя переменными монотонна, но нелинейна (например, экспоненциальная связь), то рекомендуется использовать ранговую корреляцию Спирмена , которая была разработана для хорошей обработки монотонных отношений.
Независимо от того, какой тип коэффициента корреляции вы рассчитываете, всегда полезно создать диаграмму рассеяния, чтобы визуализировать взаимосвязь между переменными.