Что такое «я» морана? (определение & #038; пример)
I Морана — это способ измерения пространственной автокорреляции.
Проще говоря, это способ количественной оценки того, насколько близко значения кластеризованы в 2D-пространстве. Он часто используется в географии и географической информатике (ГИС) для измерения того, насколько близко сгруппированы на карте различные объекты, такие как доход семьи, уровень образования и т. д.
I Морана: формула
Формула для расчета I Морана:
I = (N/W)*ΣΣw ij (x i – x )(x j – x )/Σ(x i – x ) 2
Золото:
- N: количество пространственных единиц, индексированных i и j.
- W: Сумма всех w ij
- x: переменная, представляющая интерес (доход семьи, годы обучения и т. д.).
- x : Среднее значение x
- w ij : Матрица пространственных весов
Вам, вероятно, никогда не придется рассчитывать это измерение вручную, поскольку большинство статистических программ могут рассчитать его за вас, но полезно знать формулу, используемую под капотом.
Значение I Морана может варьироваться от -1 до 1, где:
- -1: интересующая переменная идеально распределена.
- 0: интересующая переменная распределена случайным образом
- 1: интересующая переменная идеально сгруппирована
Наряду с расчетом I Морана большинство статистических программ рассчитывают соответствующее значение p, которое можно использовать для определения того, являются ли данные случайным или нет.
Тест Морана использует следующие нулевые и альтернативные гипотезы:
Нулевая гипотеза (H 0 ): данные разбросаны случайным образом.
Альтернативная гипотеза ( HA ): данные не разбросаны случайным образом, то есть сгруппированы по видимым закономерностям.
Если значение p, соответствующее I Морана, ниже определенного уровня значимости (т. е. α = 0,05), то мы можем отвергнуть нулевую гипотезу и заключить, что данные пространственно сгруппированы таким образом, что они вряд ли будут пространственно сгруппированы. произошло случайно.
I Морана: несколько примеров
Следующие примеры представляют ложные карты с разными значениями I Морана.
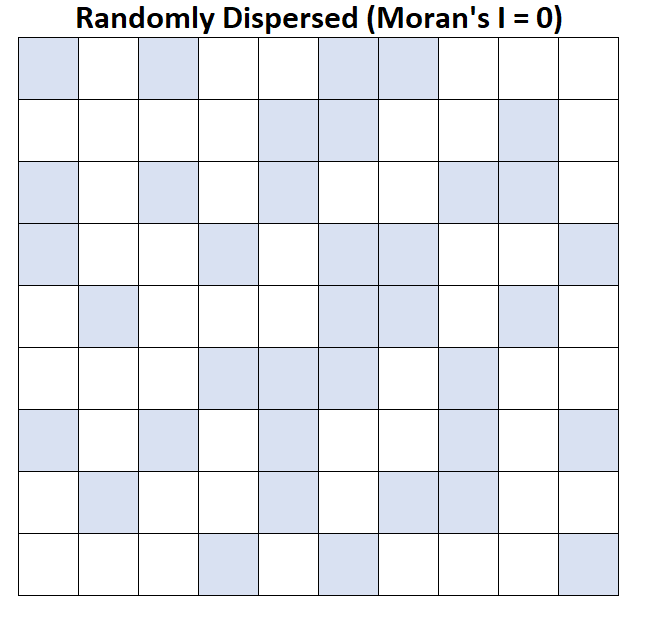
Предположим, что каждый квадрат на карте представляет округ, а округа со средним доходом семьи выше 50 000 долларов показаны синим цветом.
I Морана = 0: средний доход домохозяйства распределен случайным образом (т.е. случайные кластеры в случайных областях).
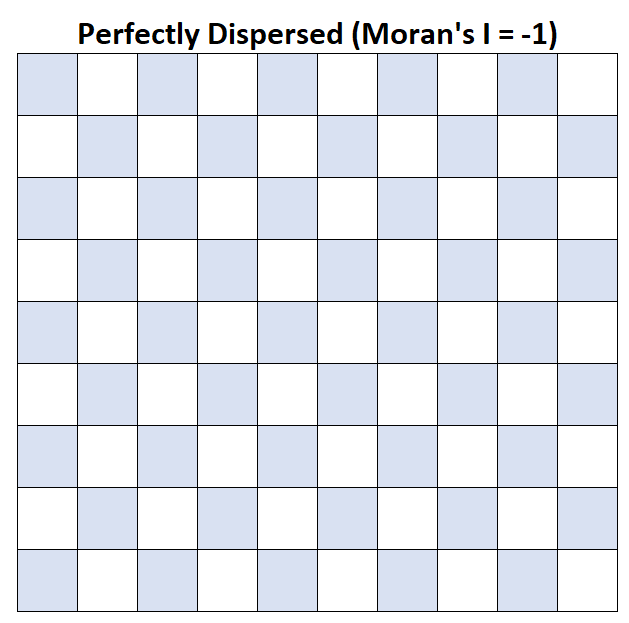
I Морана = -1: средний доход домохозяйства идеально распределен.
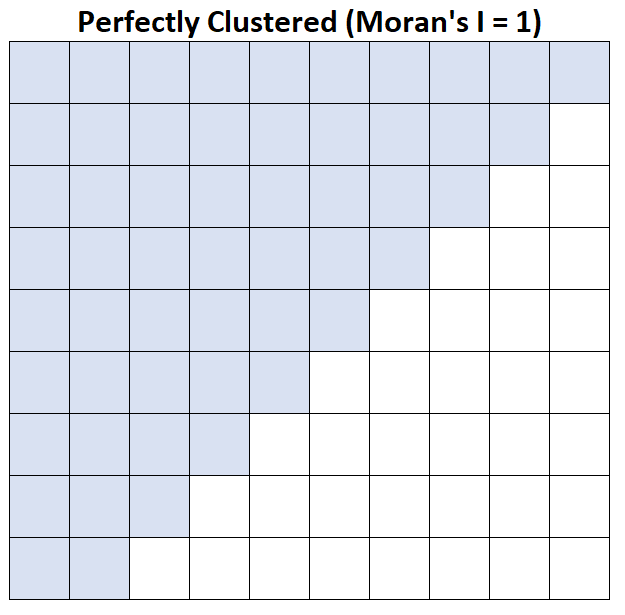
I Морана = 1: средний доход домохозяйства идеально сгруппирован.
Обратитесь к этому примеру за конкретным примером расчета I Морана в статистическом программном обеспечении R.