Частичные наименьшие квадраты в python (шаг за шагом)

Одна из наиболее распространенных проблем, с которыми вы можете столкнуться в машинном обучении, — это мультиколлинеарность . Это происходит, когда две или более переменных-предикторов в наборе данных сильно коррелируют.

Когда это происходит, модель может хорошо соответствовать набору обучающих данных, но может плохо работать с новым набором данных, которого она никогда не видела, поскольку он не соответствует набору обучающих данных. Обучающий набор.

Один из способов обойти эту проблему — использовать метод частичных наименьших квадратов , который работает следующим образом:

• Стандартизируйте переменные-предикторы и отклики.
• Вычислите M линейных комбинаций (называемых «компонентами PLS») исходных переменных-предсказателей p , которые объясняют значительную величину изменений как в переменной ответа, так и в переменных-предикторах.
• Используйте метод наименьших квадратов, чтобы подобрать модель линейной регрессии с использованием компонентов PLS в качестве предикторов.
• Используйте k-кратную перекрестную проверку , чтобы найти оптимальное количество компонентов PLS для сохранения в модели.

В этом руководстве представлен пошаговый пример выполнения метода частичных наименьших квадратов в Python.

Шаг 1. Импортируйте необходимые пакеты.

Сначала мы импортируем пакеты, необходимые для выполнения частичного метода наименьших квадратов в Python:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

Шаг 2. Загрузите данные

В этом примере мы будем использовать набор данных mtcars , который содержит информацию о 33 различных автомобилях. Мы будем использовать hp в качестве переменной ответа и следующие переменные в качестве предикторов:

• миль на галлон
• отображать
• дерьмо
• масса
• qsec

Следующий код показывает, как загрузить и отобразить этот набор данных:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

Шаг 3. Подберите модель частичных наименьших квадратов.

Следующий код показывает, как подогнать модель PLS к этим данным.

Обратите внимание, что cv = RepeatedKFold() сообщает Python использовать k-кратную перекрестную проверку для оценки производительности модели. Для этого примера мы выбираем k = 10 складок, повторяем 3 раза.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
plt. title (' hp ')

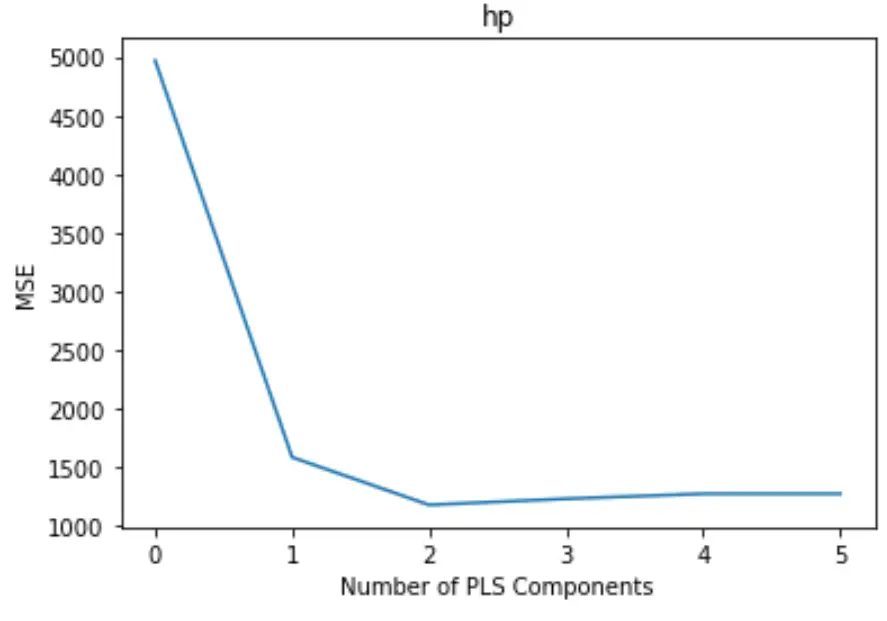
На графике отображается количество компонентов PLS по оси X и тест MSE (среднеквадратическая ошибка) по оси Y.

На графике мы видим, что MSE теста уменьшается при добавлении двух компонентов PLS, но начинает увеличиваться, когда мы добавляем более двух компонентов PLS.

Таким образом, оптимальная модель включает только первые два компонента PLS.

Шаг 4. Используйте окончательную модель для прогнозирования

Мы можем использовать окончательную модель PLS с двумя компонентами PLS, чтобы прогнозировать новые наблюдения.

В следующем коде показано, как разделить исходный набор данных на обучающий и тестовый набор и использовать модель PLS с двумя компонентами PLS для прогнозирования тестового набора.

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

Мы видим, что RMSE теста оказывается 29,9094 . Это среднее отклонение между прогнозируемым значением hp и наблюдаемым значением hp для наблюдений тестового набора.

Полный код Python, использованный в этом примере, можно найти здесь .