Как быстро найти уравнение регрессии в excel

Вы можете использовать функцию ЛИНЕЙН , чтобы быстро найти уравнение регрессии в Excel.

Эта функция использует следующий базовый синтаксис:

 LINEST(known_y's, known_x's)

Золото:

• known_y’s : столбец значений для переменной ответа
• известные_x : один или несколько столбцов значений для переменных-предикторов.

В следующих примерах показано, как использовать эту функцию для поиска уравнения регрессии для простой модели линейной регрессии и модели множественной линейной регрессии .

Пример 1. Найдите уравнение простой линейной регрессии.

Предположим, у нас есть следующий набор данных, который содержит переменную-предиктор (x) и переменную ответа (y):

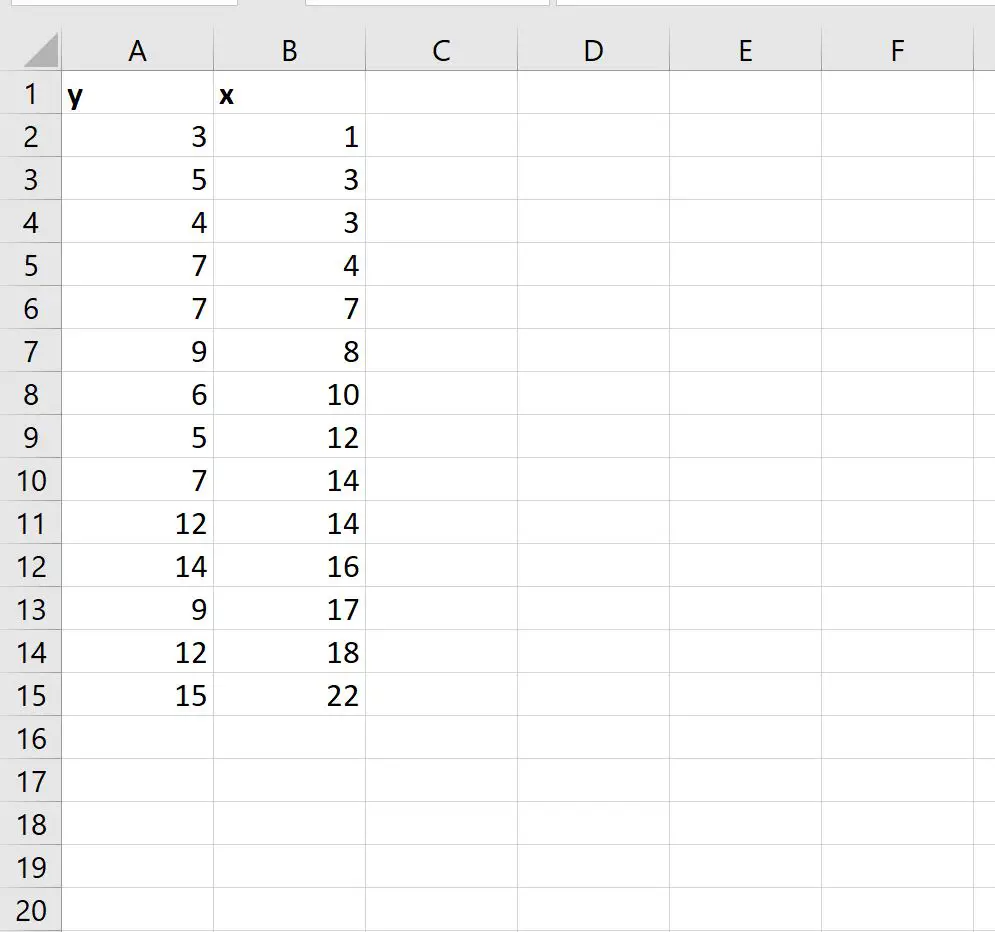
Мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить простое уравнение линейной регрессии для этого набора данных:

 =LINEST( A2:A15 , B2:B15 )

Как только мы нажмем ENTER , отобразятся коэффициенты простой модели линейной регрессии:

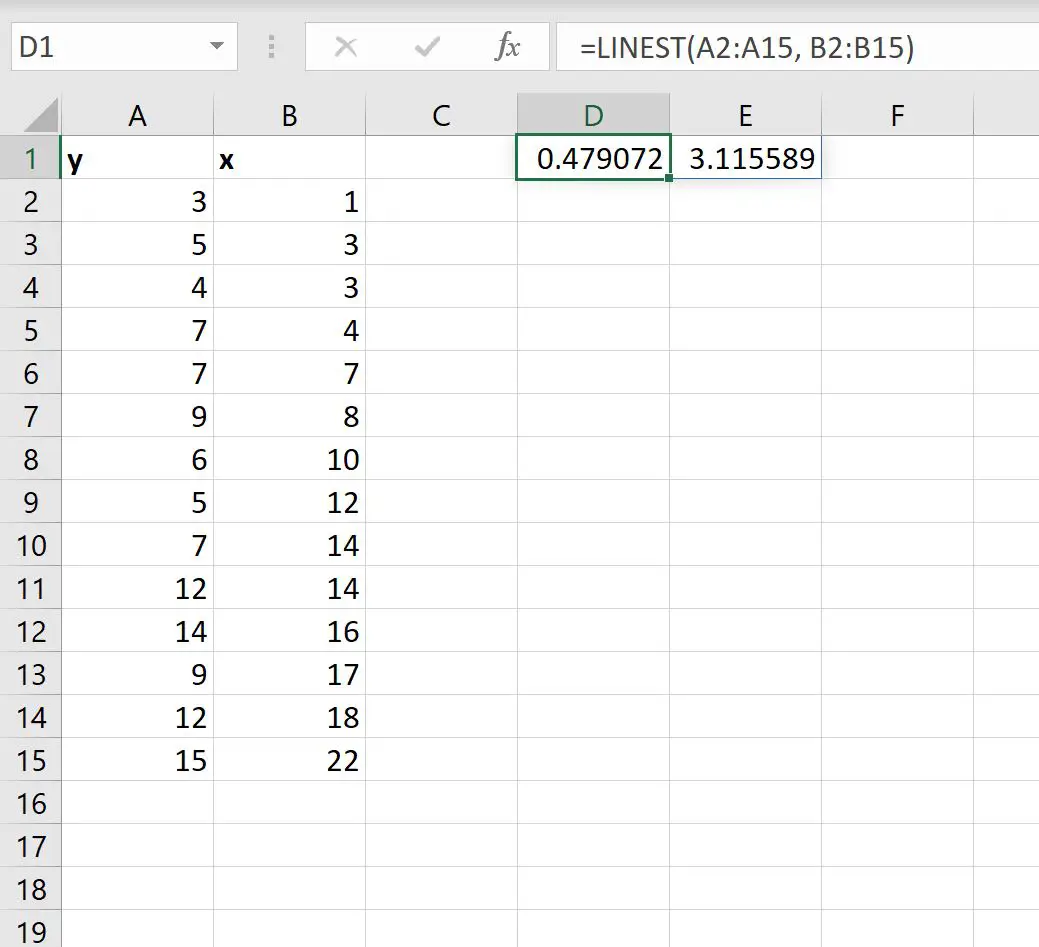
Вот как интерпретировать результат:

• Коэффициент перехвата 3,115589.
• Коэффициент наклона составляет 0,479072.

Используя эти значения, мы можем написать уравнение для этой простой модели регрессии:

у = 3,115589 + 0,478072(х)

Примечание . Чтобы найти значения p для коэффициентов, значения r-квадрата модели и других показателей, необходимо использовать функцию регрессии в пакете инструментов анализа данных. В этом уроке объясняется, как это сделать.

Пример 2. Поиск уравнения для множественной линейной регрессии

Предположим, у нас есть следующий набор данных, который содержит две переменные-предикторы (x1 и x2) и одну переменную ответа (y):

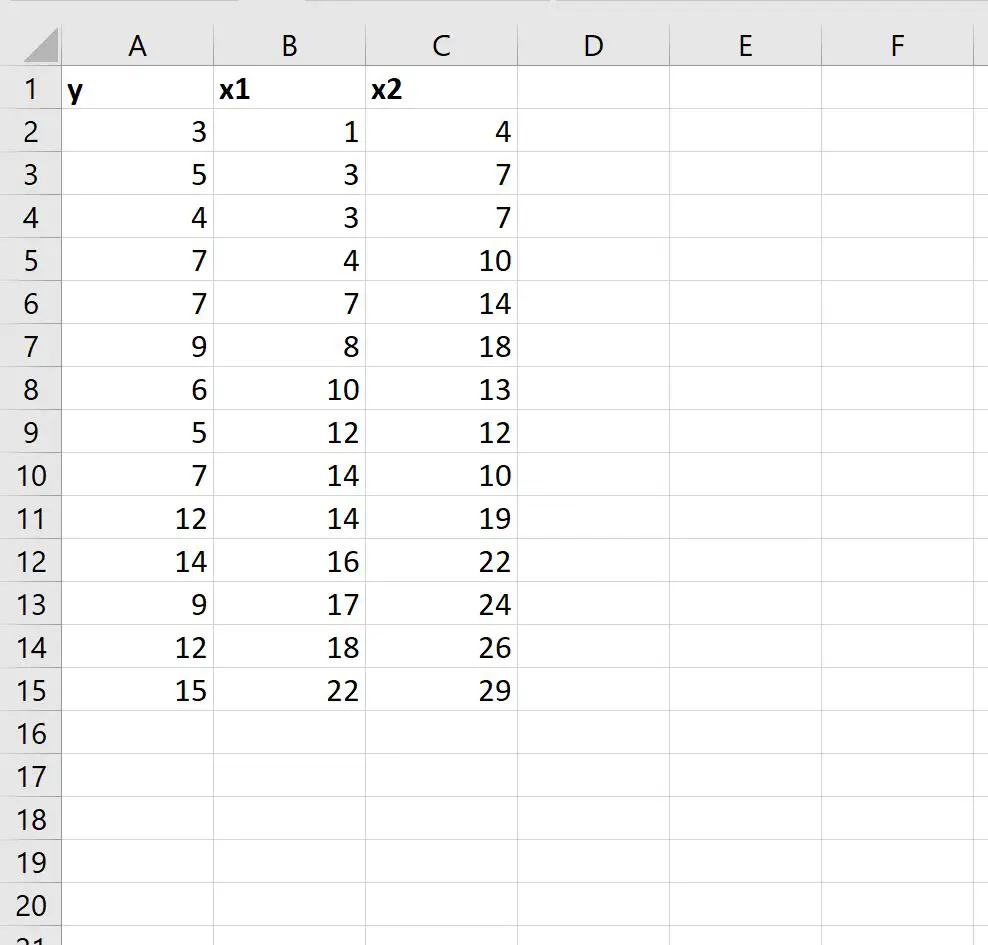
Мы можем ввести следующую формулу в ячейку E1 , чтобы вычислить уравнение множественной линейной регрессии для этого набора данных:

 =LINEST( A2:A15 , B2:C15 )

Как только мы нажмем ENTER , отобразятся коэффициенты модели множественной линейной регрессии:

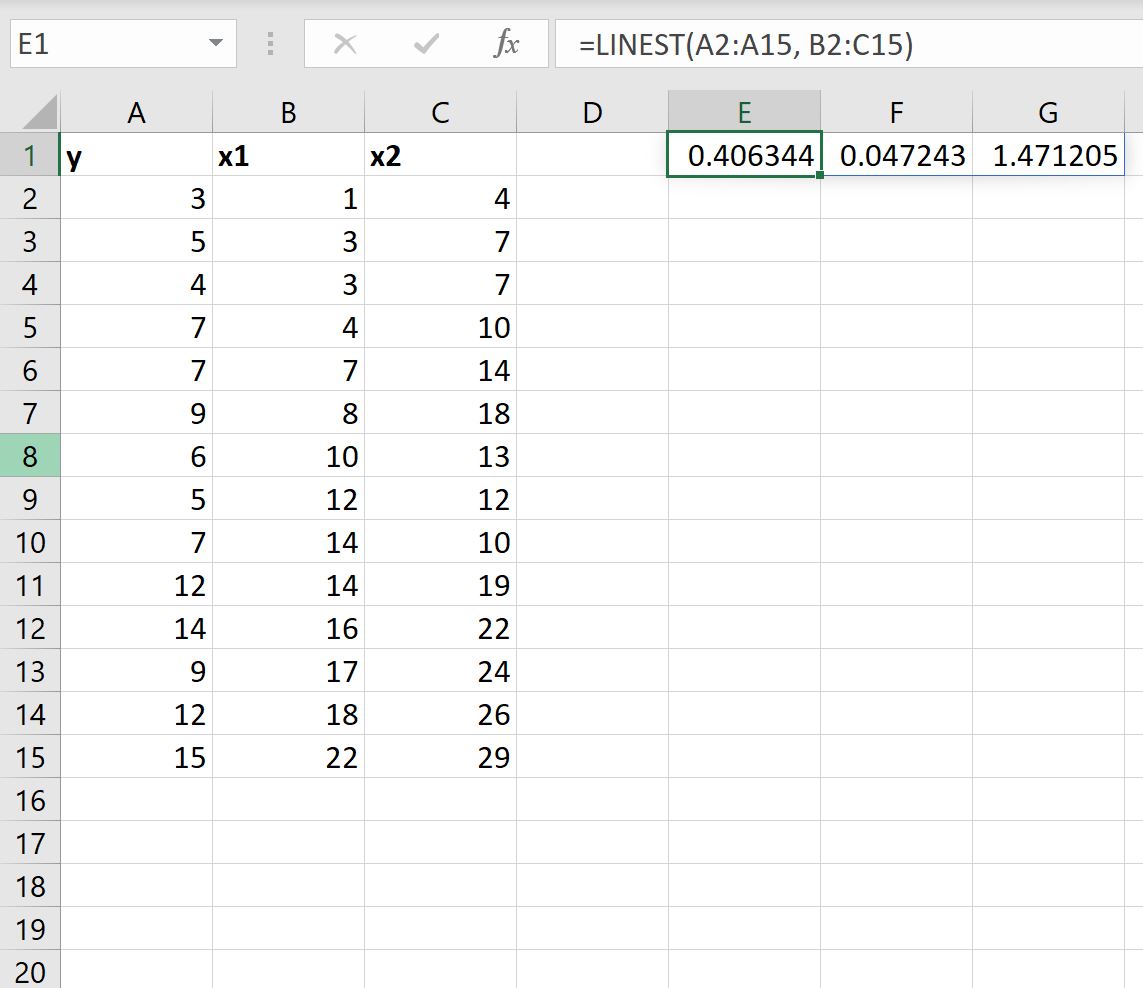
Вот как интерпретировать результат:

• Коэффициент перехвата 1,471205.
• Коэффициент при х1 равен 0,047243.
• Коэффициент при х2 равен 0,406344.

Используя эти значения, мы можем написать уравнение для этой модели множественной регрессии:

у = 1,471205 + 0,047243(х1) + 0,406344(х2)

Примечание . Чтобы найти значения p для коэффициентов, значения r-квадрата модели и других показателей для модели множественной линейной регрессии в Excel, необходимо использовать функцию «Регрессия» в пакете инструментов анализа данных. В этом уроке объясняется, как это сделать.

Дополнительные ресурсы

Следующие руководства предоставляют дополнительную информацию о регрессии в Excel:

Как интерпретировать результаты регрессии в Excel
Как добавить линию регрессии на диаграмму рассеяния в Excel
Как выполнить полиномиальную регрессию в Excel