Население означает

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что означает численность населения в статистике. Кроме того, вы узнаете, какова формула среднего значения генеральной совокупности, как рассчитывается доверительный интервал среднего значения генеральной совокупности и, кроме того, в чем разница между средним значением генеральной совокупности и средним значением «выборки».

Какова средняя численность населения?

Среднее значение генеральной совокупности представляет собой среднее арифметическое всех элементов статистической совокупности. Следовательно, чтобы вычислить среднее значение совокупности, все значения совокупности необходимо сложить, а затем разделить на общее количество элементов в совокупности.

Обозначением средней численности населения является греческая буква μ.

Аналогичным образом, среднее значение популяции также можно определить как ожидаемое значение переменной, представляющей совокупность.

Как рассчитать среднюю численность населения

После того, как мы увидели определение среднего значения численности населения, давайте посмотрим, как рассчитывается среднее значение численности населения, чтобы лучше понять его значение.

Если все значения статистической совокупности известны, для расчета среднего значения генеральной совокупности следует просто применить формулу среднего арифметического. Итак, в этом случае, чтобы вычислить среднее значение численности населения, нам нужно сложить все значения численности населения, а затем разделить на общее количество данных.

Таким образом, если мы знаем значение всех элементов генеральной совокупности, формула для расчета среднего значения генеральной совокупности будет следующей:

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ См.: Пример вычисления среднего арифметического.

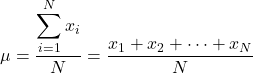
Однако в целом не все значения совокупности известны, поэтому обычно значение средней совокупности оценивается по интервалам .

Доверительный интервал для генерального среднего значения

На практике невозможно изучить всех особей в популяции, поэтому обычно выбирается случайная выборка популяции и на основе ее значений делается аппроксимация значения среднего значения популяции. Точнее, мы вычисляем интервал, в котором, скорее всего, находится среднее значение всей совокупности; этот интервал называется доверительным интервалом для среднего значения генеральной совокупности.

Доверительный интервал для среднего значения генеральной совокупности рассчитывается путем сложения и вычитания из выборочного среднего значения Z _α/2 , умноженного на стандартное отклонение (σ) и деленного на квадратный корень из высоты выборки (n). Следовательно, формула для расчета доверительного интервала для среднего генерального значения выглядит следующим образом:

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

Приведенная выше формула используется, когда известна дисперсия генеральной совокупности. Однако если дисперсия генеральной совокупности неизвестна, что является наиболее распространенным случаем, доверительный интервал для среднего значения рассчитывается по следующей формуле:

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

Золото:

$\overline{x}$

это образец означает.
$t_{\alpha/2}$

— значение t-распределения Стьюдента n-1 степеней свободы с вероятностью α/2. Для больших размеров выборки и уровня достоверности 95% оно обычно близко к 1,96, а для уровня достоверности 99% оно обычно близко к 2,576.
$s$

— выборочное стандартное отклонение.
$n$

это размер выборки.

➤ См.: Пример расчета доверительного интервала для среднего значения генеральной совокупности.

Среднее генеральное и выборочное среднее

Наконец, подводя итог, мы рассмотрим различия между средним значением генеральной совокупности и средним значением выборки, чтобы эти две статистические концепции были понятны.

Разница между средним значением генеральной совокупности и средним значением выборки представляет собой диапазон значений, по которому рассчитывается среднее значение. Среднее значение генеральной совокупности — это среднее значение всей статистической совокупности, тогда как среднее выборочное — это среднее значение выборки совокупности.

Кроме того, чтобы отличить среднее значение совокупности от среднего значения выборки, они представлены разными символами. Символ численности населения:

$\mu$

, с другой стороны, символ выборки означает

$\overline{x}$

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

Если у вас все еще есть сомнения относительно различий между этими двумя типами средних значений или вы хотите узнать больше о расчете выборочного среднего значения, вы можете обратиться к следующей статье:

➤ См.: Что означает выборка?

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше