Что такое сомерс д? (определение & #038; пример)
D Сомерса , сокращение от Дельта Сомерса, является мерой силы и направления связи между порядковой зависимой переменной и порядковой независимой переменной.
Порядковая переменная — это переменная, в которой значения имеют естественный порядок (например, «плохой», «нейтральный», «хороший»).
Значение D Сомерса находится в диапазоне от -1 до 1, где:
- -1: указывает на то, что все пары переменных не согласуются.
- 1: указывает, что все пары переменных совпадают.
D Сомерса используется на практике для многих непараметрических статистических методов.
Сомерс Д: определение
Учитывая две переменные, X и Y, мы можем сказать:
- Две пары (x i , y i ) и (x j , y j ) согласованы , если ранги двух элементов совпадают.
- Две пары (x i , y i ) и (x j , y j ) несогласны. если ранги двух элементов совпадают.
Затем мы можем рассчитать D Сомерса, используя следующую формулу:
D Сомерса = ( NC – ND ) / ( NC + ND + NT )
Золото:
- NC : количество совпадающих пар.
- ND : количество несогласованных пар.
- N T : количество связанных пар.
Результирующее значение всегда будет между -1 и 1.
Somers’ D: пример в R
Предположим, продуктовый магазин хочет оценить взаимосвязь между следующими двумя порядковыми переменными:
- Общее дружелюбие кассира (оценки от 1 до 3)
- Общая удовлетворенность клиентов (также оценивается от 1 до 3)
Они собирают следующие оценки по выборке из 10 клиентов:
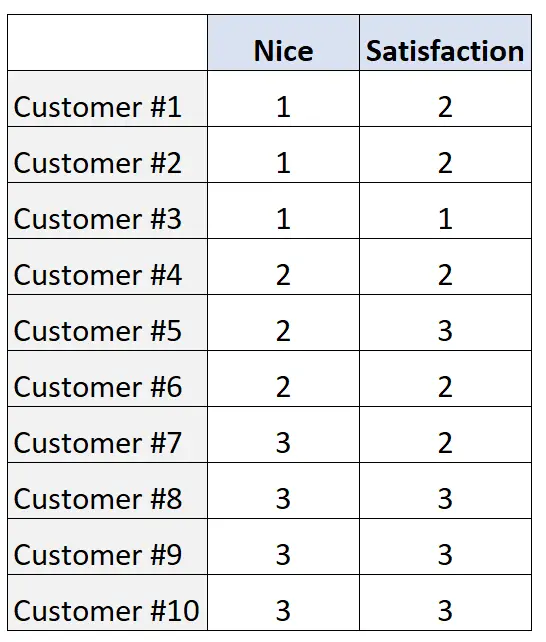
Чтобы количественно оценить взаимосвязь между двумя переменными, мы можем вычислить D Сомерса, используя следующий код в R:
#enter data nice <- c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3) satisfaction <- c(2, 2, 1, 2, 3, 2, 2, 3, 3, 3) #load DescTools package library(DescTools) #calculate Somers' D SomersDelta(nice, satisfaction) [1] 0.6896552
D Сомерса оказывается равным 0,6896552 .
Поскольку это значение довольно близко к 1, это указывает на довольно сильную положительную связь между двумя переменными.
Это интуитивно понятно: клиенты, которые оценивают кассиров как более приятных, также склонны выше оценивать свою общую удовлетворенность.
Дополнительные ресурсы
Введение в коэффициент корреляции Пирсона
Введение в Тау Кендалла