R кратный или r квадратный: в чем разница?
Когда вы подгоняете модель регрессии с помощью большинства статистических программ, вы часто замечаете в результате следующие два значения:
Множественный R: коэффициент множественной корреляции между тремя или более переменными.
R-квадрат: рассчитывается как (Multiple R) 2 и представляет собой долю дисперсии переменной отклика регрессионной модели, которую можно объяснить переменными-предикторами. Это значение варьируется от 0 до 1.
На практике нас часто интересует значение R-квадрата, поскольку оно говорит нам, насколько полезны переменные-предикторы для прогнозирования значения переменной отклика.
Однако каждый раз, когда мы добавляем в модель новую предикторную переменную, R-квадрат гарантированно увеличивается, даже если предикторная переменная бесполезна.
Скорректированный R-квадрат — это модифицированная версия R-квадрата, которая корректирует количество предикторов в регрессионной модели. Он рассчитывается следующим образом:
Скорректированный R 2 = 1 – [(1-R 2 )*(n-1)/(nk-1)]
Золото:
- R 2 : R 2 модели.
- n : Количество наблюдений
- k : Количество переменных-предсказателей
Поскольку R-квадрат всегда увеличивается по мере добавления в модель большего количества предикторов, скорректированный R-квадрат может служить показателем, который говорит вам, насколько полезна модель, скорректированная на основе количества предикторов в модели .
Чтобы лучше понять каждый из этих терминов, рассмотрим следующий пример.
Пример: множественный R, R-квадрат и скорректированный R-квадрат.
Предположим, у нас есть следующий набор данных, который содержит следующие три переменные для 12 разных студентов:
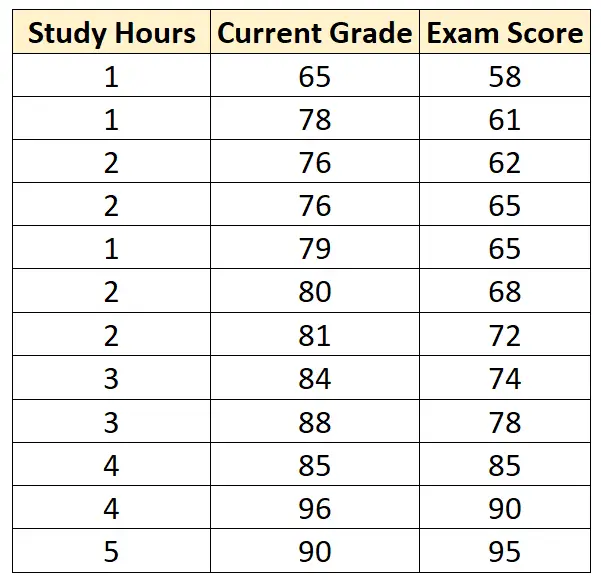
Предположим, мы подбираем модель множественной линейной регрессии, используя часы обучения и текущую оценку в качестве переменных-предсказателей, а оценку на экзамене в качестве переменной ответа, и получаем следующий результат:
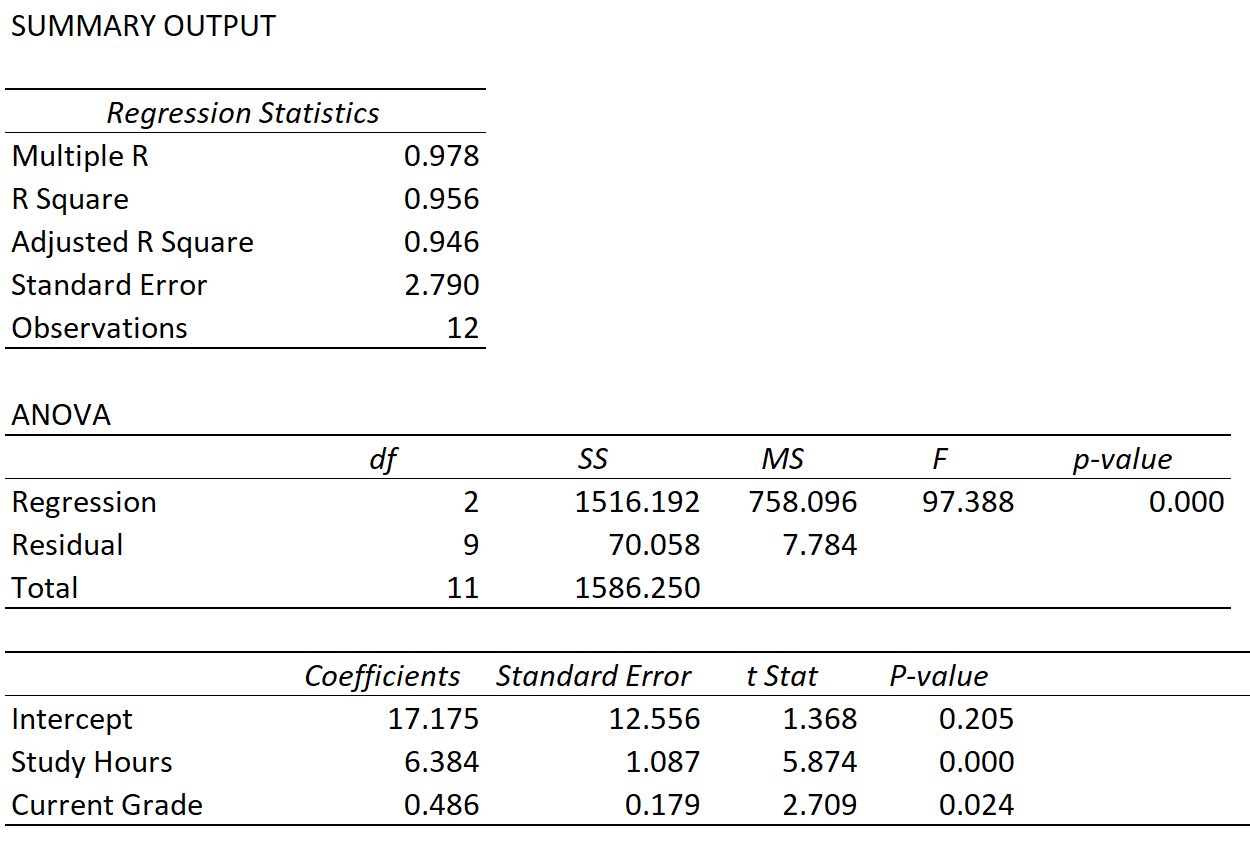
Мы можем наблюдать значения следующих трех показателей:
Множественный R: 0,978 . Это представляет собой множественную корреляцию между переменной ответа и двумя переменными-предикторами.
R Квадрат: 0,956 . Это рассчитывается как (Множественное R) 2 = (0,978) 2 = 0,956. Это говорит нам о том, что 95,6% различий в результатах экзаменов можно объяснить количеством часов, потраченных студентами на обучение, и их текущей оценкой по курсу.
Скорректированный R-квадрат: 0,946 . Это рассчитывается следующим образом:
Скорректированный R 2 = 1 – [(1-R 2 )*(n-1)/(nk-1)] = 1 – [(1-.956)*(12-1)/(12-2-1) ] = 0,946.
Это представляет собой значение R-квадрата, скорректированное с учетом количества переменных-предикторов в модели .
Эта мера была бы полезна, если, например, мы подогнали другую модель регрессии с 10 предикторами и обнаружили, что скорректированный R-квадрат этой модели составил 0,88 . Это указывает на то, что модель регрессии только с двумя предикторами лучше, поскольку она имеет более высокое скорректированное значение R-квадрата.
Дополнительные ресурсы
Введение в множественную линейную регрессию
Что такое хорошее значение R-квадрата?