4 примера отсутствия корреляции между переменными

В статистике корреляция — это мера линейной связи между двумя переменными.

Значение коэффициента корреляции всегда находится в диапазоне от -1 до 1, где:

• -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
• 0 указывает на отсутствие линейной корреляции между двумя переменными.
• 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.

Если две переменные имеют нулевую корреляцию, это указывает на то, что они никак не связаны. Другими словами, знание значения одной переменной не дает нам представления о том, каким может быть значение другой переменной.

Если мы создадим диаграмму рассеяния двух переменных, имеющих нулевую корреляцию, на графике не будет четкой закономерности:

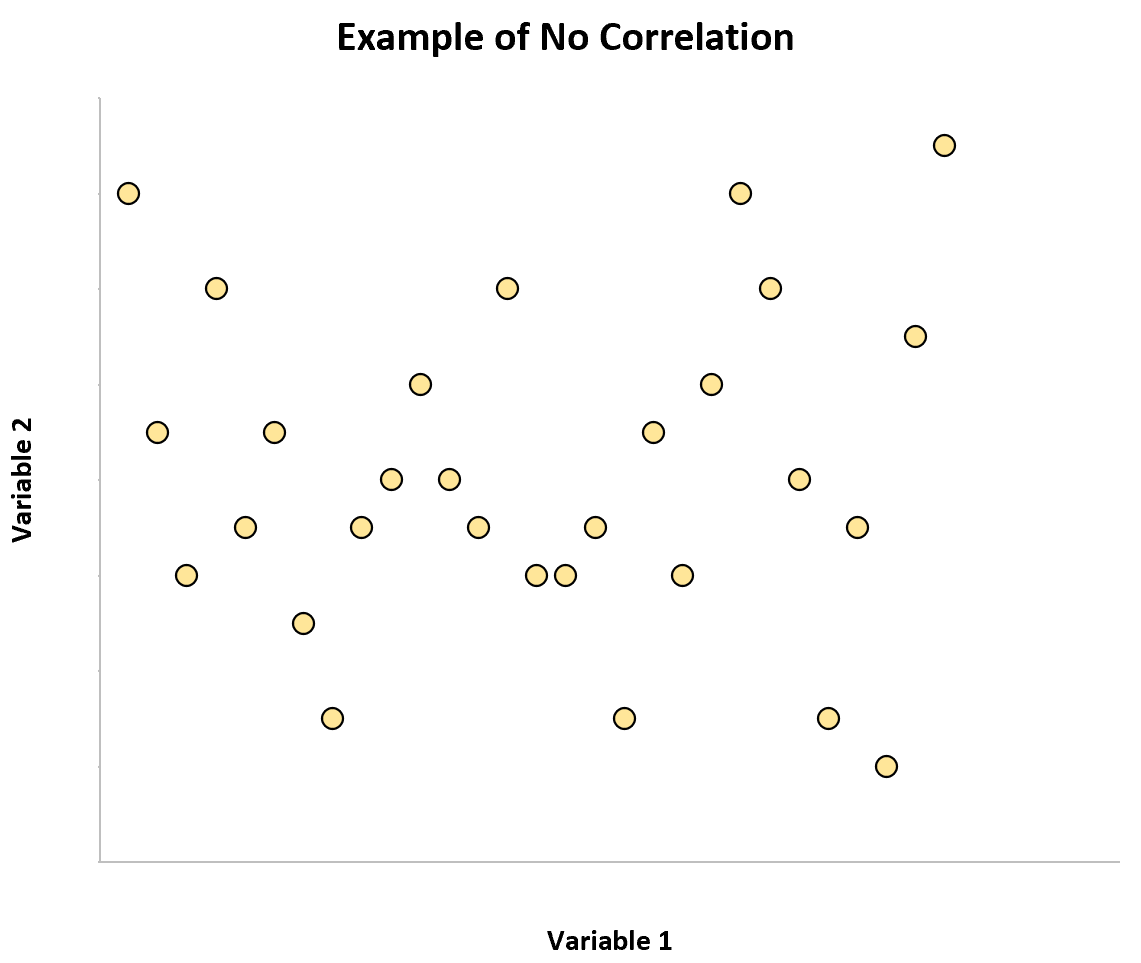
Примеры отсутствия корреляции

Следующие примеры иллюстрируют сценарии, в которых две переменные не имеют корреляции.

Пример 1: Потребление кофе и интеллект

Количество кофе, потребляемого людьми, и их уровень IQ имеют нулевую корреляцию. Другими словами, знание того, сколько кофе выпивает человек, не дает нам представления об уровне его IQ.

Если бы мы создали диаграмму рассеяния ежедневного потребления кофе в зависимости от уровня IQ, она выглядела бы так:

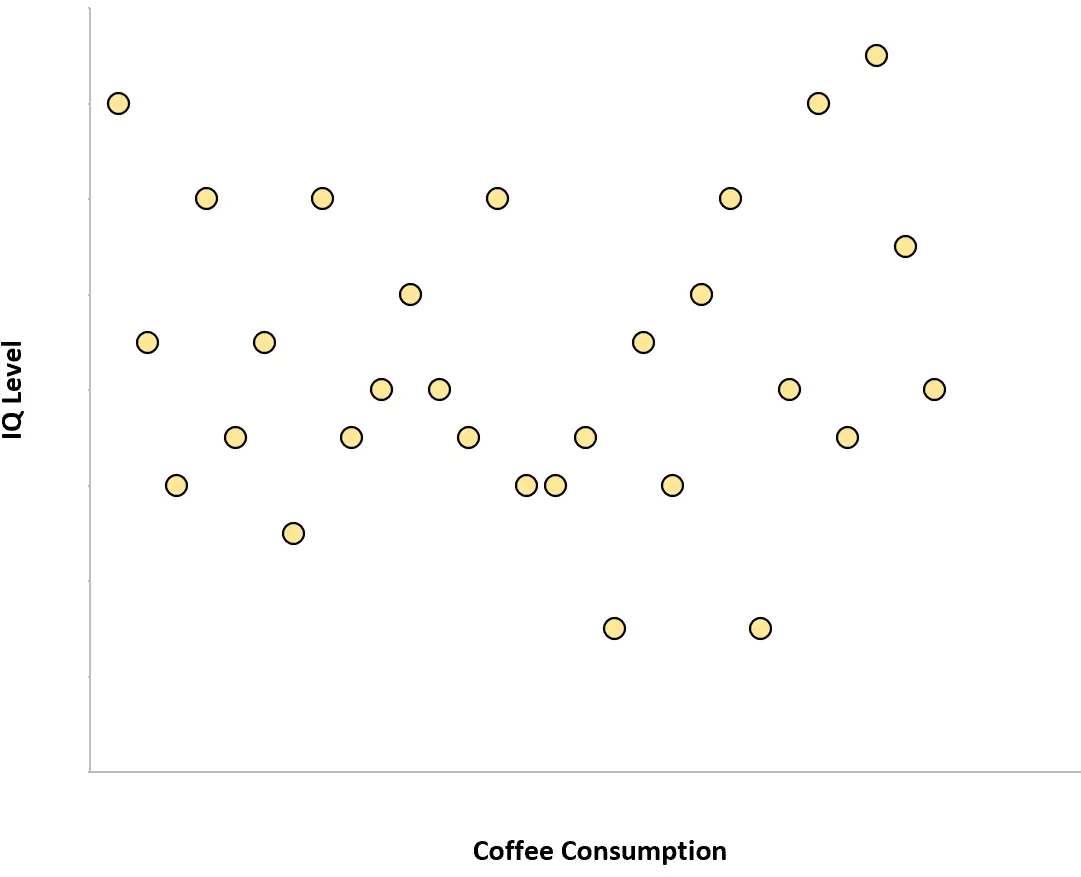
Пример 2: Рост и результаты тестов

Рост учащихся и их средние результаты тестов имеют нулевую корреляцию. Другими словами, знание роста человека не дает нам представления о его среднем балле на экзамене.

Если бы мы создали диаграмму рассеяния, представляющую рост в зависимости от среднего балла на экзамене, она выглядела бы так:

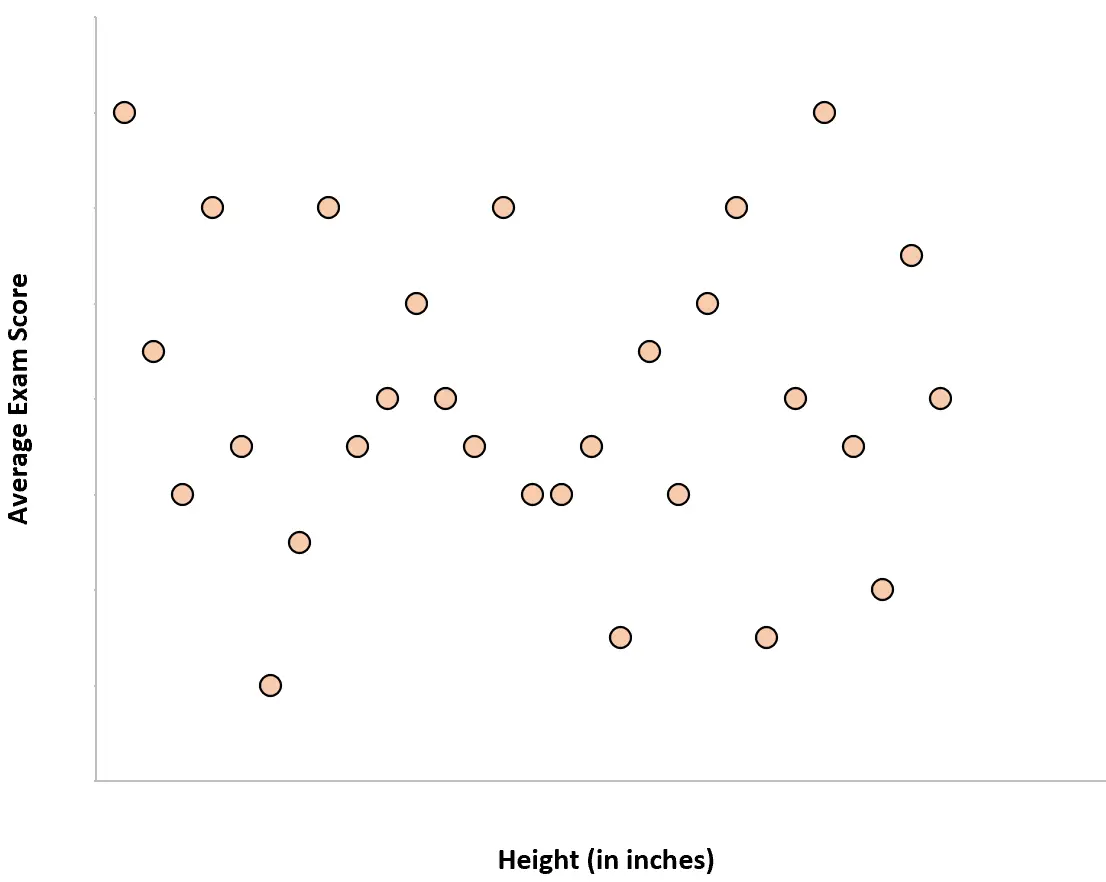
Пример 3: размер обуви и просмотренные фильмы

Размер обуви людей и количество фильмов, которые они смотрят в год, не имеют нулевой корреляции. Другими словами, знание размера обуви человека не дает нам представления о том, сколько фильмов он смотрит в год.

Если бы мы построили диаграмму зависимости размера обуви от количества просмотренных фильмов, она выглядела бы так:

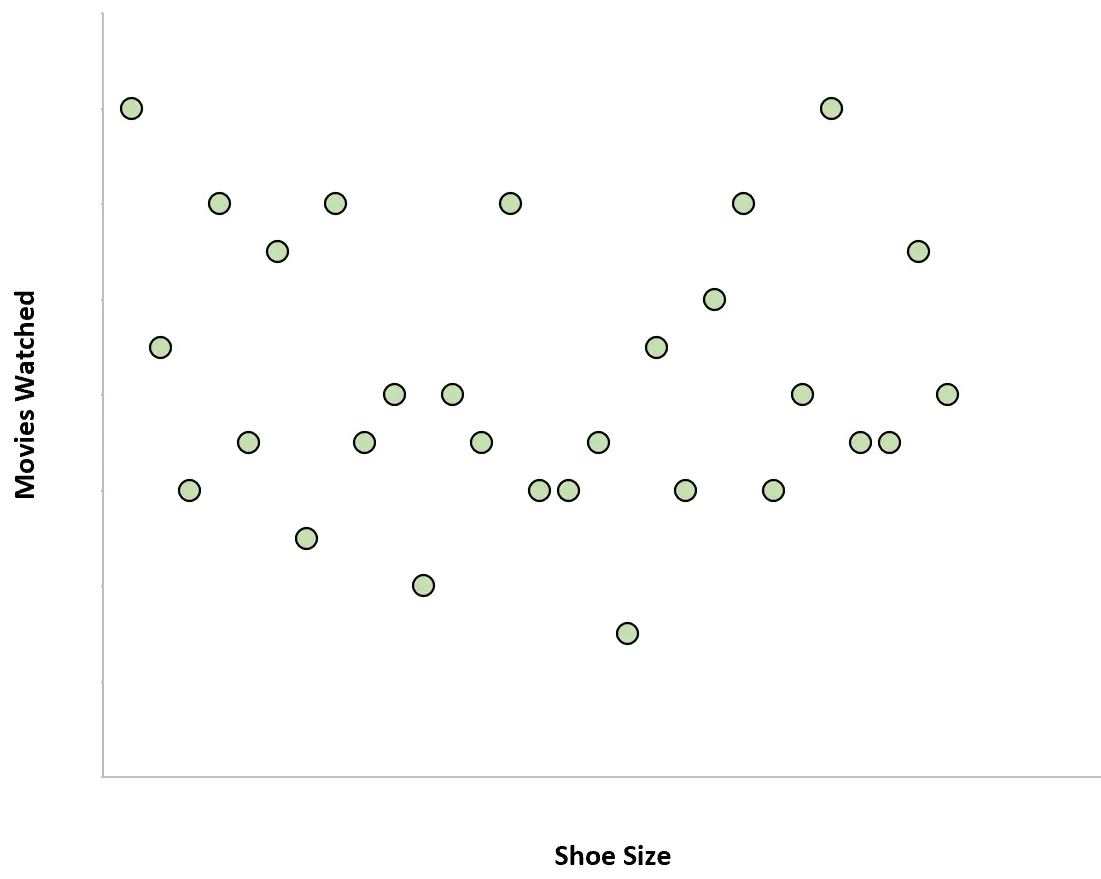
Пример 4: вес и доход

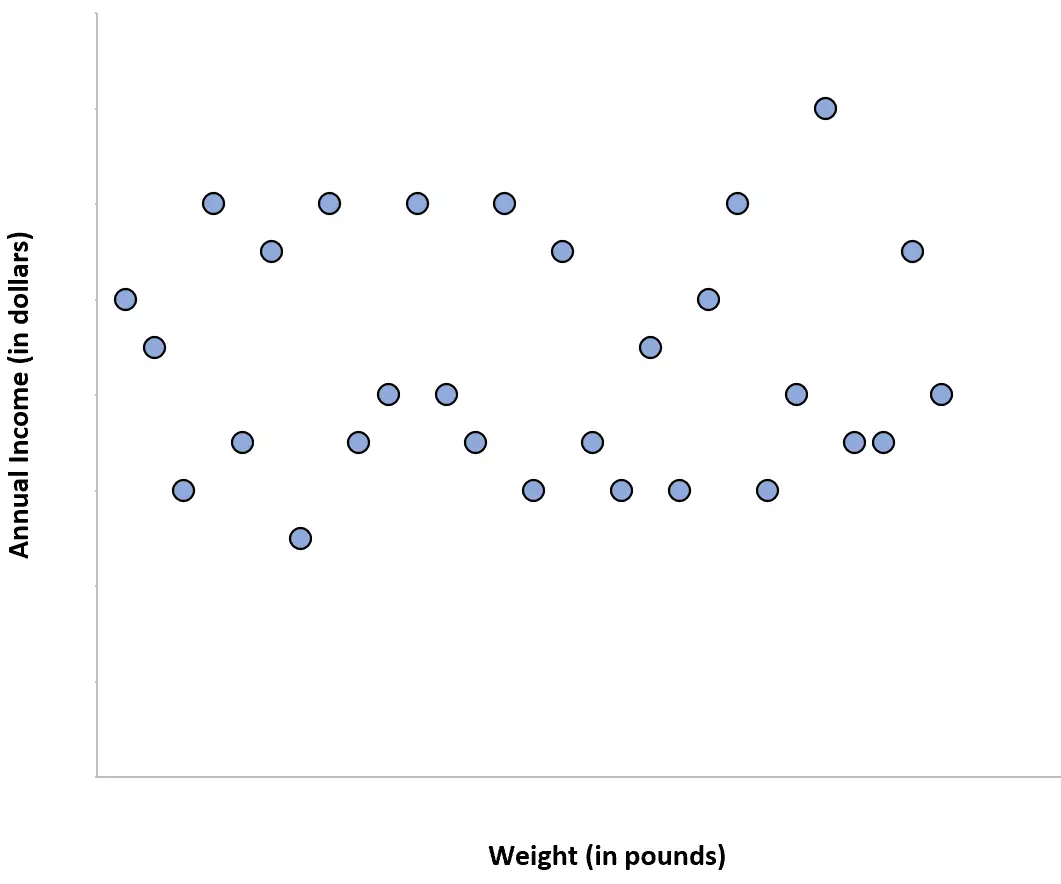
Вес людей и их годовой доход имеют нулевую корреляцию. Другими словами, знание веса человека не дает нам представления о том, каким может быть его годовой доход.

Если бы мы создали диаграмму рассеяния веса/дохода, она выглядела бы так:

Дополнительные ресурсы

Введение в коэффициент корреляции Пирсона
Корреляция против. ассоциация: в чем разница?
Корреляция и регрессия: в чем разница?