Нормальное распределение

К бенджамин андерсон 3 августа, 2023 Вероятность 0 комментариев

В этой статье объясняется, что такое нормальное распределение в статистике. Итак, вы найдете определение нормального распределения, примеры нормального распределения и каковы свойства нормального распределения.

Что такое нормальное распределение?

Нормальное распределение — это непрерывное распределение вероятностей, график которого имеет колоколообразную форму и симметричен относительно своего среднего значения. В статистике нормальное распределение используется для моделирования явлений с очень разными характеристиками, поэтому это распределение так важно.

Фактически, в статистике нормальное распределение считается наиболее важным из всех распределений вероятностей, поскольку оно не только позволяет моделировать большое количество явлений реального мира, но и может использоваться для аппроксимации других типов распределений. распределения. при определенных условиях.

Символом нормального распределения является заглавная буква N. Итак, чтобы указать, что переменная подчиняется нормальному распределению, она обозначается буквой N, а в скобках добавляются значения ее среднего арифметического и стандартного отклонения.

$X\sim N(\mu,\sigma)$

Нормальное распределение имеет много разных названий, включая распределение Гаусса , распределение Гаусса и распределение Лапласа-Гаусса .

Примеры нормального распределения

Обычно наборы данных, которые соответствуют нормальному распределению, содержат большое количество наблюдений и охватывают очень общие темы. Ниже приведены несколько примеров статистических выборок, которые обычно можно смоделировать с помощью нормального распределения.

Примеры нормального распределения:

Численность студентов на курсе.
IQ работников компании.
Количество бракованных деталей, изготовленных на заводе за день.
Оценки, полученные на экзамене студентами курса.
Доходность акций компаний, котирующихся на фондовой бирже.

График нормального распределения

После того, как мы увидели, что такое нормальное распределение и некоторые примеры этого типа распределения вероятностей, давайте посмотрим, как выглядит его график, чтобы лучше понять концепцию.

На следующем графике вы можете увидеть, как меняется функция плотности нормального распределения в зависимости от значений ее среднего арифметического и стандартного отклонения.

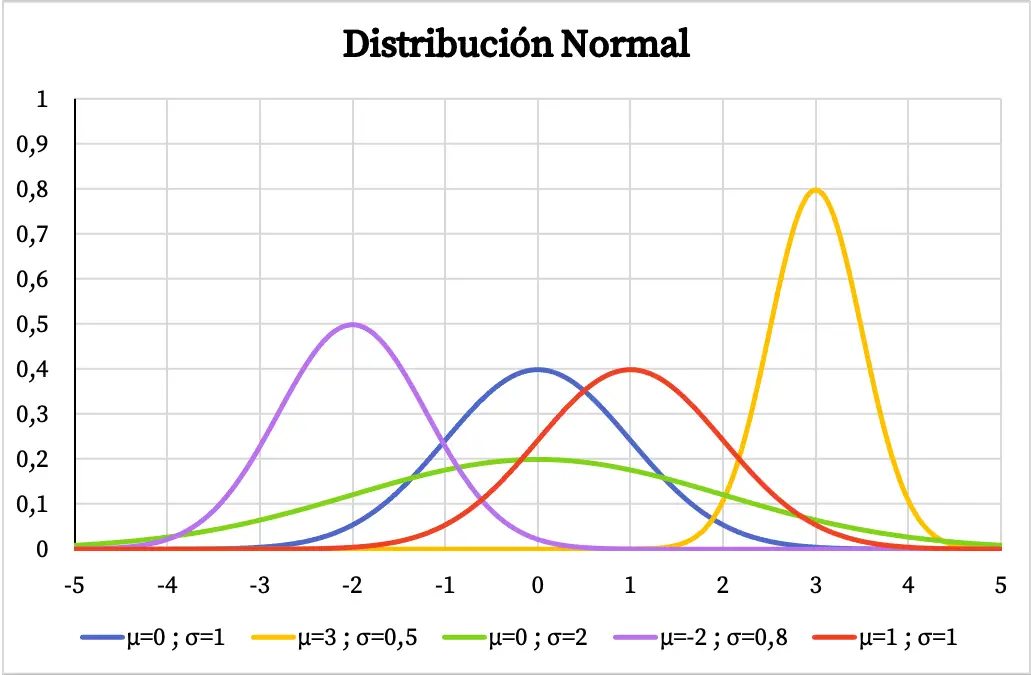
Имея форму колокола с центром в среднем арифметическом, если переменная имеет нормальное распределение, это означает, что наиболее повторяющееся значение является средним и что значения вокруг среднего повторяются чаще, чем экстремальные значения. Аналогично, чем больше стандартное отклонение нормального распределения, тем более плоская форма его графического представления.

С другой стороны, график кумулятивной функции вероятности нормального распределения также зависит от значений ее среднего арифметического и стандартного отклонения, как вы можете видеть на следующем изображении:

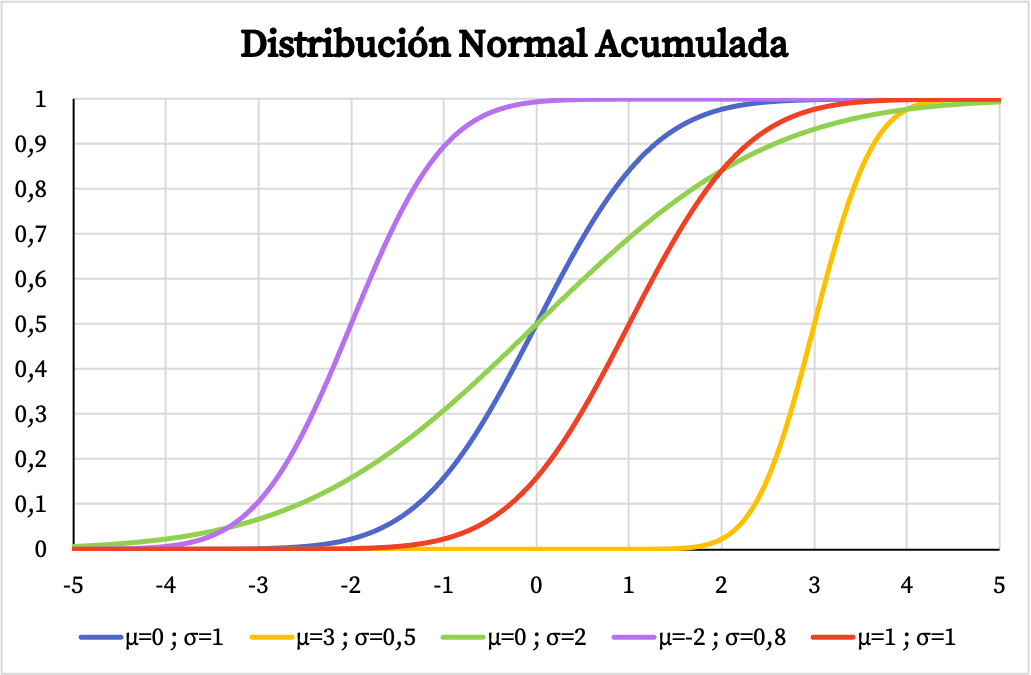
Функция плотности и функция распределения нормального распределения позволяют рассчитать вероятности, связанные с этим распределением. Однако вместо использования их формул вы можете напрямую использовать таблицы нормального распределения, поскольку это быстрее. С этими таблицами можно ознакомиться по следующей ссылке:

➤ См.: Таблица нормального распределения.

Характеристики нормального распределения

Нормальное распределение имеет следующие характеристики:

Нормальное распределение зависит от двух характерных параметров: среднего арифметического (μ) и стандартного отклонения (σ).

$X\sim N(\mu,\sigma)$

Нормальное распределение может принимать положительные и отрицательные значения, поэтому областью нормального распределения являются действительные числа.

$x\in \mathbb{R}$

Медиана и мода нормального распределения равны среднему арифметическому распределению.

$Me=Mo=\mu$

Коэффициент асимметрии и коэффициент эксцесса нормального распределения равны нулю.

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

Формула функции плотности нормального распределения:

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

Аналогично, формула для кумулятивной функции вероятности нормального распределения:

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

Применение центральной предельной теоремы состоит в том, что распределение Пуассона может приближаться к нормальному распределению, когда значение λ достаточно велико.

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

Другое применение центральной предельной теоремы состоит в том, что биномиальное распределение можно аппроксимировать нормальным распределением для наборов данных с большим количеством наблюдений.

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

Стандартное нормальное распределение

Стандартное нормальное распределение , также называемое единичным нормальным распределением , является простейшим случаем нормального распределения. Точнее, стандартное нормальное распределение — это нормальное распределение со значениями среднего и стандартного отклонения, равными 0 и 1 соответственно.

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Обратите внимание, что любое нормальное распределение можно преобразовать в стандартное нормальное распределение, применив процесс, называемый типированием, который включает в себя вычитание среднего арифметического значения из каждого значения и затем деление на его стандартное отклонение.

Кроме того, стандартное нормальное распределение используется для определения любой вероятности нормального распределения с использованием его таблицы вероятностей. Итак, чтобы найти вероятность нормального распределения, сначала вводится переменная, чтобы преобразовать ее к стандартному нормальному распределению, а затем мы смотрим в таблицу, чтобы узнать, каково соответствующее значение вероятности. Чтобы узнать больше, нажмите на следующую ссылку:

➤ См.: Стандартное нормальное распределение.