Как рассчитать вероятности normalcdf в excel
Функция NormalCDF на калькуляторе TI-83 или TI-84 может использоваться для определения вероятности того, что нормально распределенная случайная величина примет значение в определенном диапазоне.
На калькуляторе TI-83 или TI-84 эта функция использует следующий синтаксис:
нормальныйcdf (нижний, верхний, µ, σ)
Золото:
- нижняя = нижнее значение диапазона
- верхний = верхнее значение диапазона
- μ = среднее значение численности населения
- σ = стандартное отклонение генеральной совокупности
Например, предположим, что случайная величина обычно распределяется со средним значением 50 и стандартным отклонением 4. Вероятность того, что случайная величина примет значение от 48 до 52, можно рассчитать следующим образом:
нормальныйcdf(48, 52, 50, 4) = 0,3829
Мы можем воспроизвести этот ответ в Excel, используя функцию НОРМ.РАСП() , которая использует следующий синтаксис:
НОРМ.РАСП(x, σ, μ, совокупное)
Золото:
- x = индивидуальное значение данных
- μ = среднее значение численности населения
- σ = стандартное отклонение генеральной совокупности
- накопительный = ЛОЖЬ рассчитать PDF; TRUE вычисляет CDF
Следующие примеры показывают, как использовать эту функцию на практике.
Пример 1: Вероятность между двумя значениями
Предположим, что случайная величина обычно распределяется со средним значением 50 и стандартным отклонением 4. Вероятность того, что случайная величина примет значение от 48 до 52, можно рассчитать следующим образом:
=NORM. DIST (52, 50, 4, TRUE ) - NORM. DIST (48, 50, 4, TRUE )
На следующем изображении показано, как выполнить этот расчет в Excel:
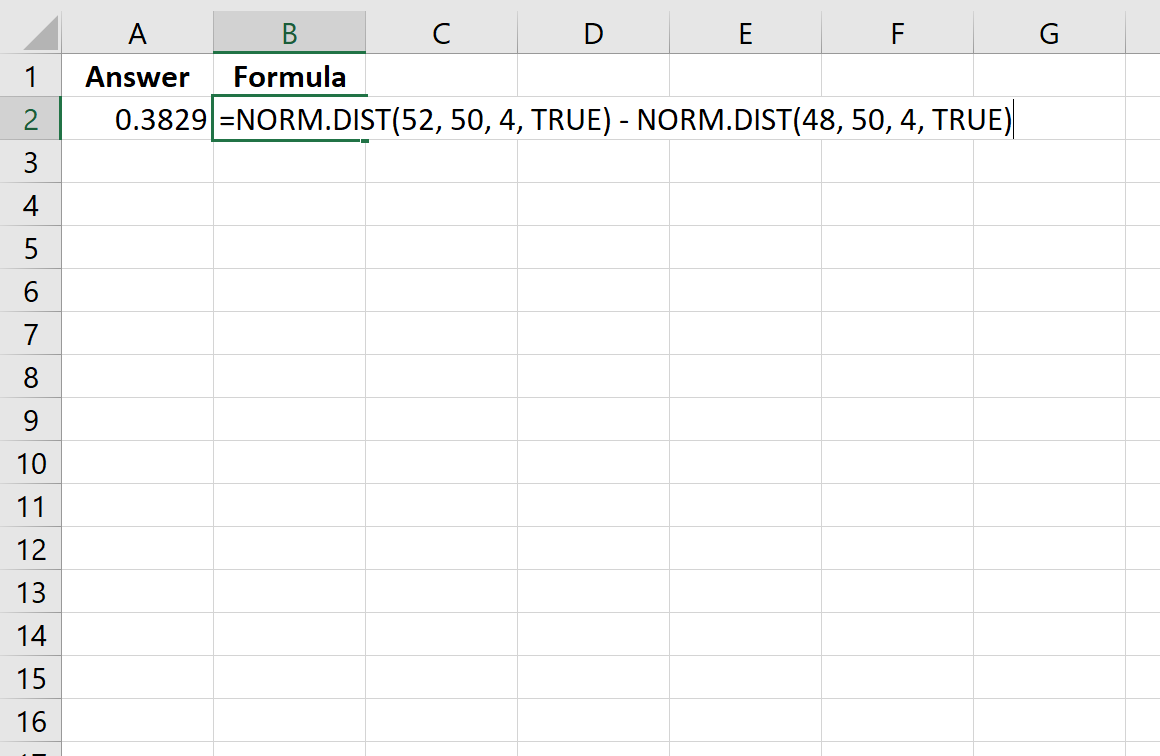
Вероятность оказывается 0,3829.
Пример 2: Вероятность меньше одного значения
Предположим, что случайная величина обычно распределяется со средним значением 50 и стандартным отклонением 4. Вероятность того, что случайная величина примет значение меньше 48, можно рассчитать следующим образом:
=NORM. DIST (48, 50, 4, TRUE )
На следующем изображении показано, как выполнить этот расчет в Excel:
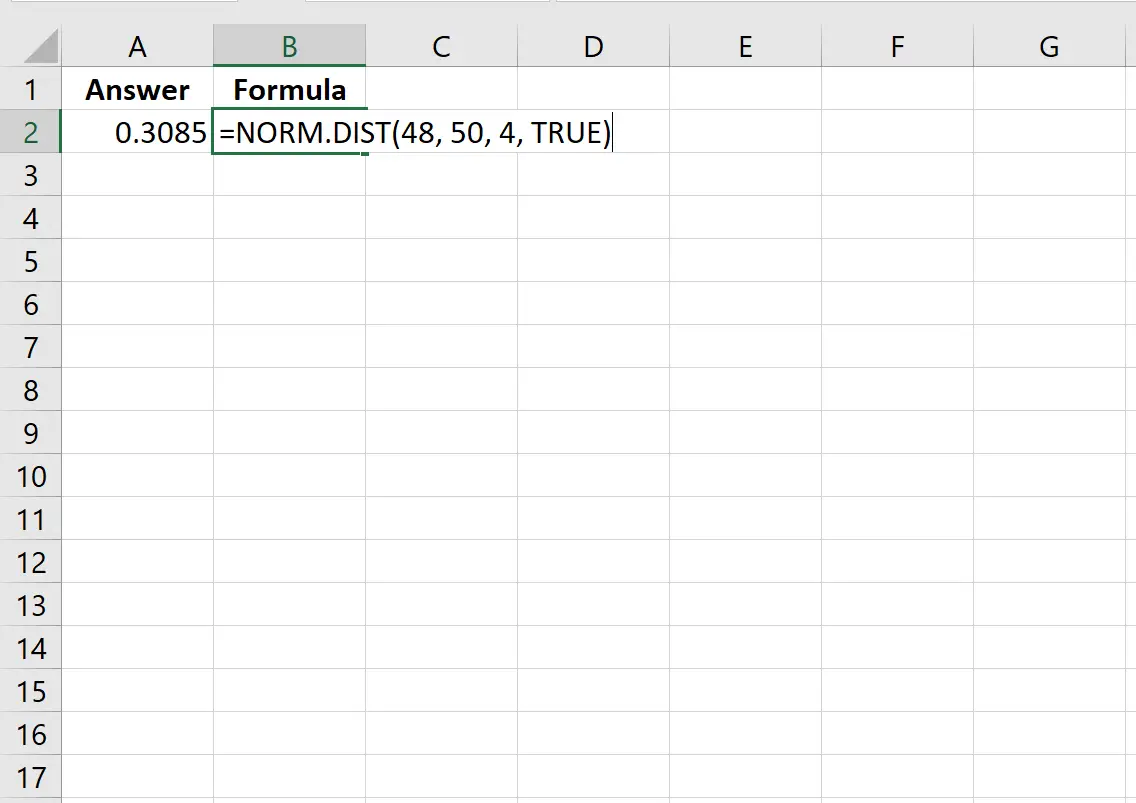
Вероятность оказывается равной 0,3085.
Пример 3: Вероятность больше значения
Предположим, что случайная величина обычно распределяется со средним значением 50 и стандартным отклонением 4. Вероятность того, что случайная величина примет значение больше 55, можно рассчитать следующим образом:
=1 - NORM. DIST (55, 50, 4, TRUE )
На следующем изображении показано, как выполнить этот расчет в Excel:
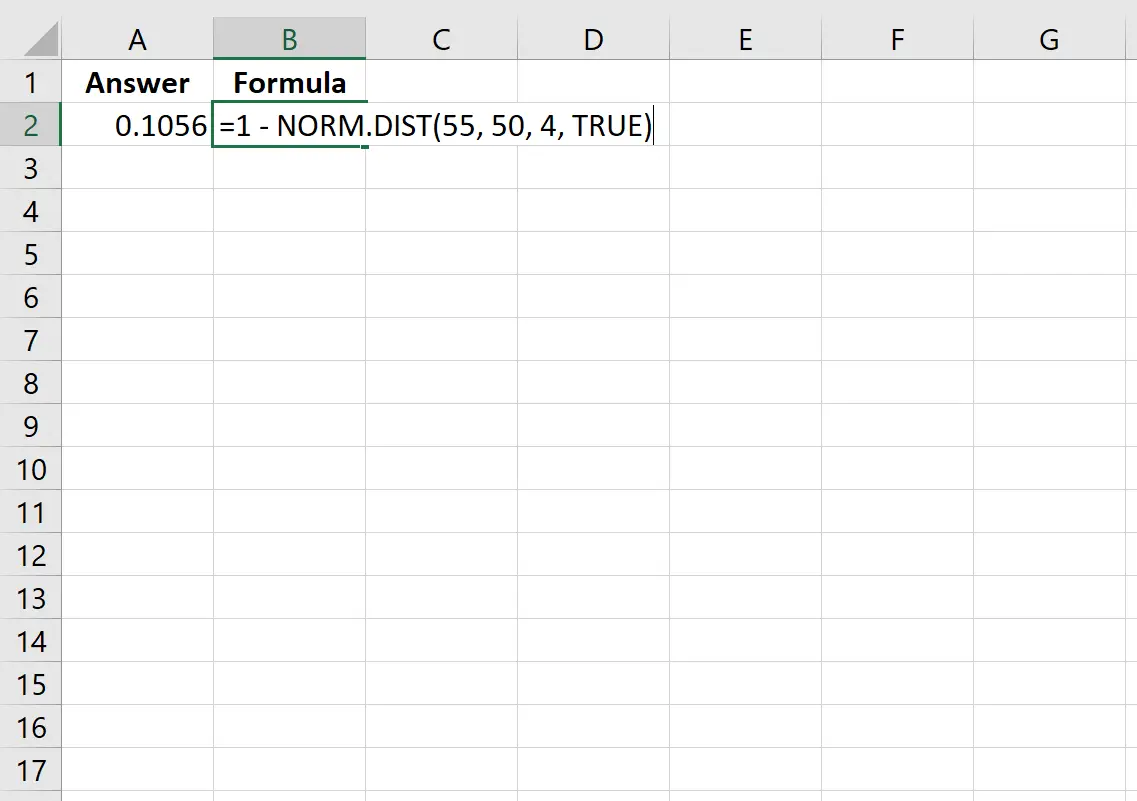
Вероятность оказывается 0,1056.
Дополнительные ресурсы
Вы также можете использовать этот обычный калькулятор CDF , чтобы автоматически найти вероятности, связанные с нормальным распределением.