Операции над множествами: объединение, пересечение, дополнение и разность.
Набор — это совокупность элементов.
Мы обозначаем набор заглавной буквой и определяем элементы набора с помощью фигурных скобок. Например, предположим, что у нас есть набор под названием «A» с элементами 1, 2, 3. Мы бы написали это следующим образом:
А = {1, 2, 3}
В этом руководстве объясняются наиболее часто используемые операции над множествами в теории вероятности и статистике.
союз
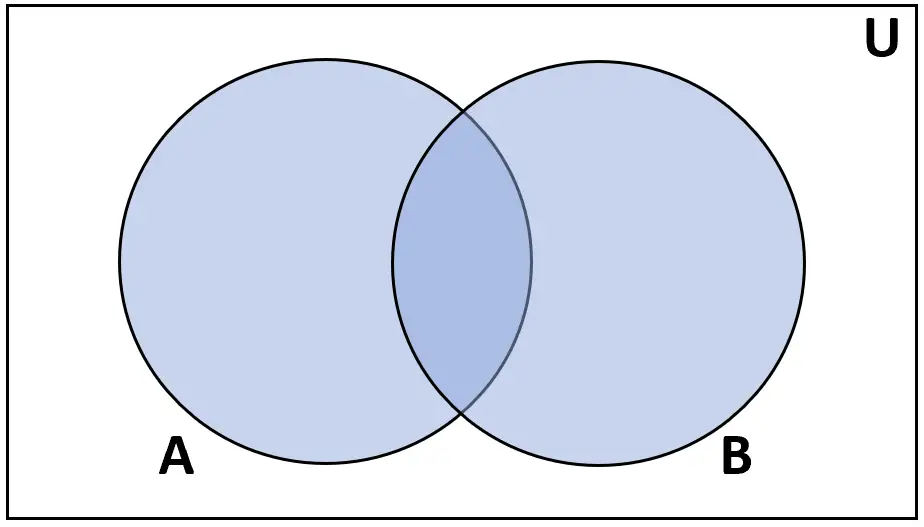
Определение: Объединение множеств A и B — это множество элементов, найденных либо в A, либо в B.
Рейтинг: А ∪ Б
Примеры:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
Пересечение
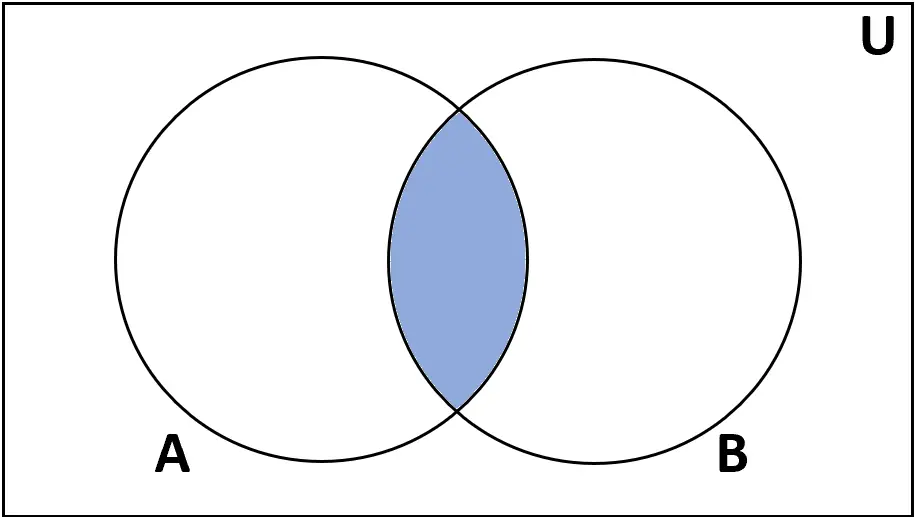
Определение: Пересечение множеств A и B — это набор элементов, которые встречаются как в A, так и в B.
Обозначение: А ∩ B
Примеры:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
Дополнить
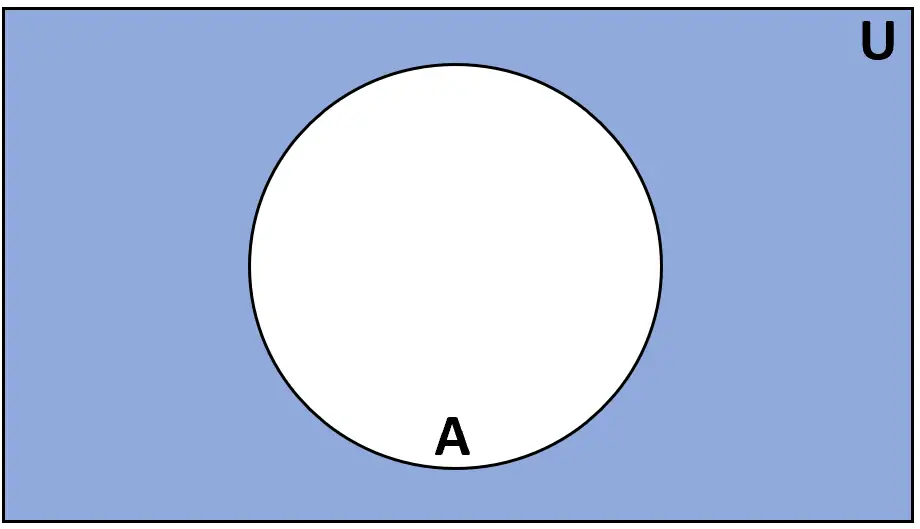
Определение: Дополнением множества A является множество элементов, которые входят в универсальное множество U, но не входят в A.
Рейтинг: A’ или Ac
Примеры:
- Если U = {1, 2, 3, 4, 5, 6} и A = {1, 2}, то A c = {3, 4, 5, 6}
- Если U = {1, 2, 3} и A = {1, 2}, то A c = {3}
Разница
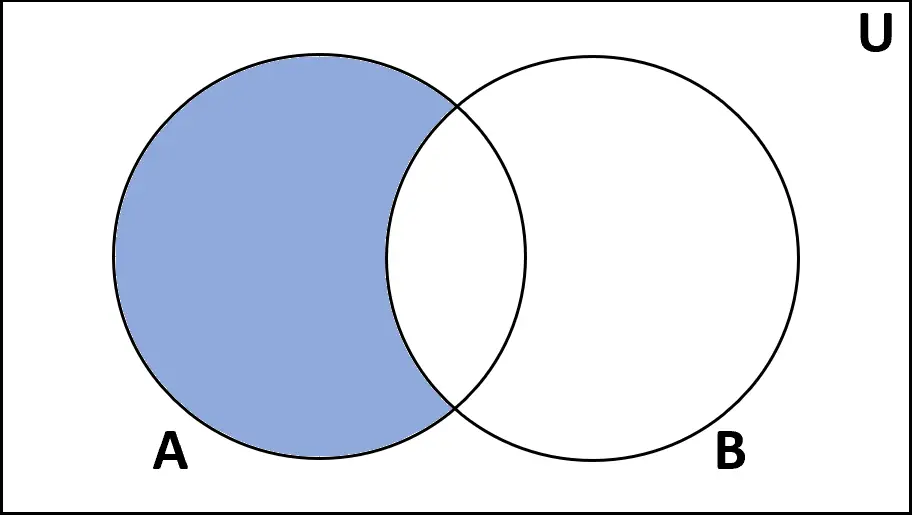
Определение: Разница между множествами A и B — это набор элементов, которые встречаются в A, но не встречаются в B.
Рейтинги: A–B.
Примеры:
- {1, 2, 3} – {2, 3, 4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
Симметричная разница
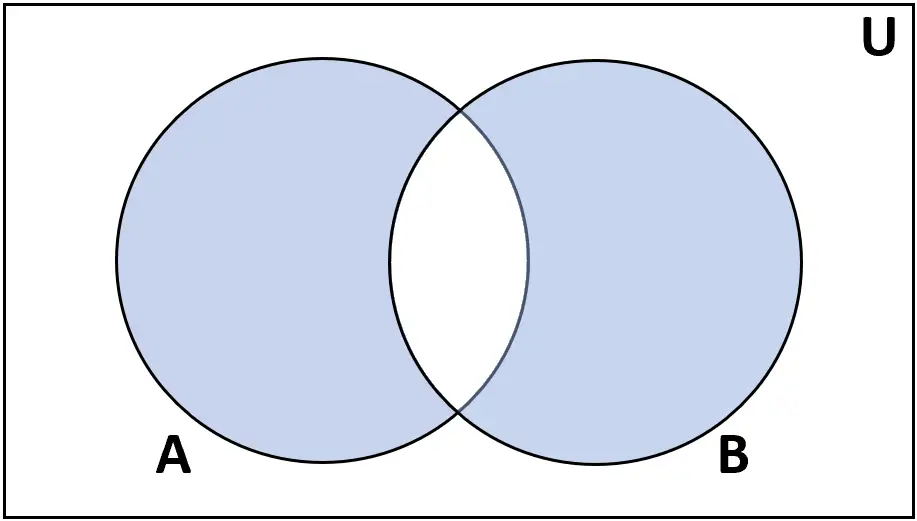
Определение: Симметричная разность множеств A и B — это набор элементов, которые встречаются либо в A, либо в B, но не в обоих.
Рейтинг: AΔB
Примеры:
- {1, 2, 3} Δ {2, 3, 4} = {1, 4}
- {1, 2} Δ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
Декартово произведение
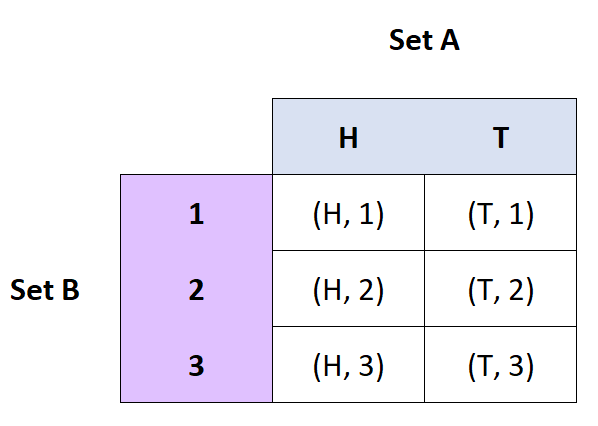
Определение: Декартово произведение множеств A и B — это множество упорядоченных пар A и B.
Рейтинг: А х Б
Примеры:
- Если A = {H, T} и B = {1, 2, 3}, то A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( Т, 2), (Т, 3)}
- Если A = {T, H} и B = {1, 2, 3}, то A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( Ч, 2), (Ч, 3)}