Что такое ограничение объема?

Часто в статистике мы стремимся измерить корреляцию между двумя переменными. Это помогает нам понять следующее:

• Направление связи между двумя переменными. При увеличении одной переменной имеет ли тенденцию к увеличению или уменьшению другая переменная?
• Сила связи между двумя переменными. Насколько изменится значение двух переменных?

К сожалению, проблема, которая может возникнуть при измерении корреляции между двумя переменными, называется ограничением диапазона . Это происходит, когда диапазон измеряемых значений одной из переменных по каким-либо причинам ограничен.

Например, предположим, что мы хотим измерить корреляцию между учебными часами и результатами экзаменов учащихся конкретной школы.

Если мы соберем данные по этим двум переменным для всех 1000 учащихся школы, мы можем обнаружить, что корреляция между учебными часами и оценками на экзаменах составляет 0,73 .

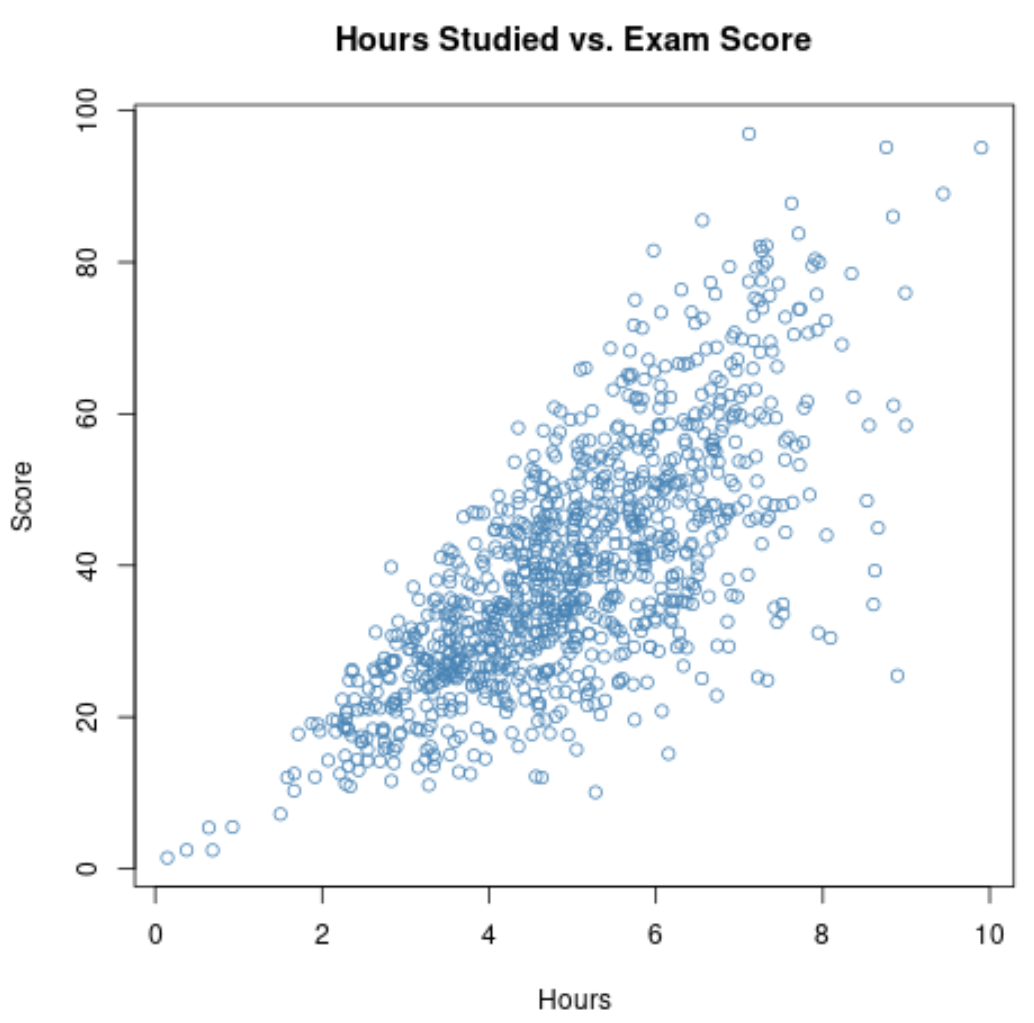
Эта корреляция довольно высока, что указывает на сильную положительную связь между двумя переменными. Чем больше студенты учатся, тем лучше они сдают экзамены.

Однако давайте предположим, что мы собираем данные только о студентах курсов с отличием. Возможно, все эти студенты учились не менее 6 часов.

Таким образом, если мы рассчитаем корреляцию между учебными часами и баллами на экзаменах для этих студентов, мы будем использовать узкий диапазон для переменных учебных часов .

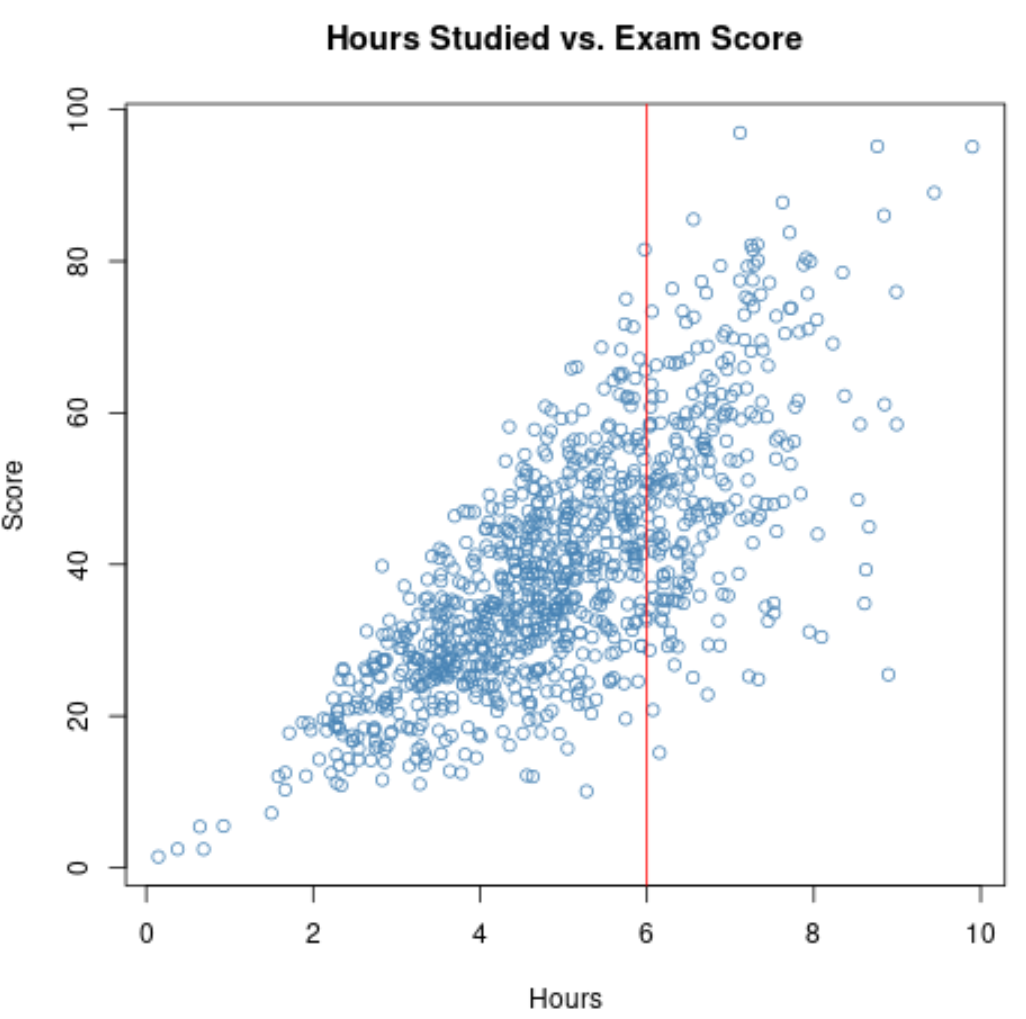
Если мы увеличим диаграмму рассеяния для диапазона, в котором часы больше 6, график будет выглядеть следующим образом:

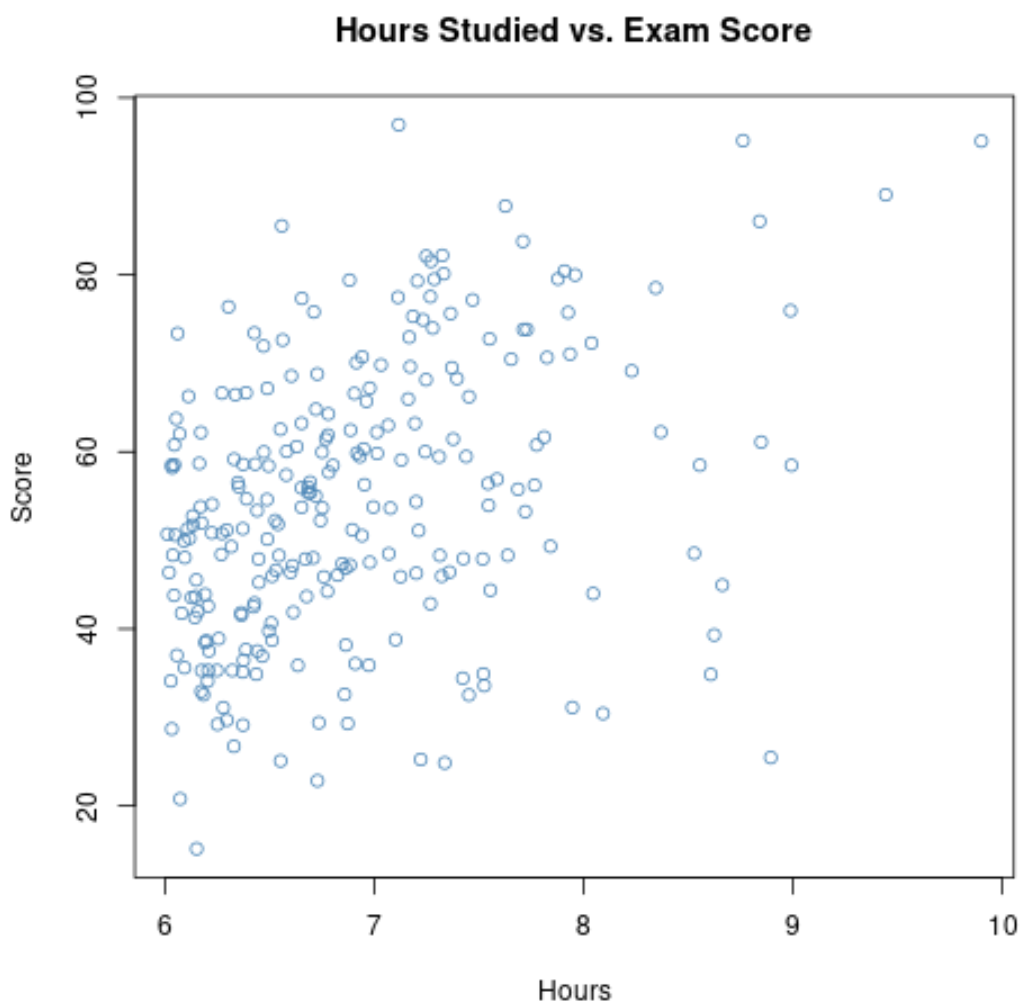
Корреляция между двумя переменными на этом графике оказывается равной 0,37 , что значительно ниже 0,73 .

Таким образом, если бы мы собирали данные только об учебных часах и результатах экзаменов для студентов курсов с отличием, мы могли бы предположить, что существует слабая связь между учебными часами и экзаменационными баллами.

Однако этот результат может ввести в заблуждение, поскольку мы использовали ограниченный диапазон для одной из переменных.

Реальные примеры ограниченного диапазона

Проблема ограниченного диапазона может возникнуть на практике во многих различных исследованиях. Вот некоторые примеры:

1. Исследования высококвалифицированных спортсменов . Исследователям может быть интересно узнать, производит ли определенная программа тренировок больше мышечной массы, чем определенная стандартная программа.

Если исследователи собирают данные только об элитных спортсменах, вполне вероятно, что все эти спортсмены уже имеют высокую мышечную массу. Таким образом, для расчета корреляции между программой тренировок и наработанной мышечной массой будет доступен узкий диапазон значений.

2. Обучение отличников. Исследователи, возможно, захотят изучить, оказывает ли определенная программа репетиторства положительное влияние на оценки. По своей природе студенты, стремящиеся улучшить свои оценки и принять участие в программе репетиторства, могут уже быть хорошо успевающими учениками.

Таким образом, возможностей для улучшения оценок этих учащихся, возможно, не так уж и много. Когда исследователи рассчитывают корреляцию между часами, проведенными в программе репетиторства, и полученным в результате повышением оценок, истинная корреляция может быть недооценена, поскольку возможности для улучшения оценок ограничены.

Как учитывать ограниченные диапазоны

Популярный способ учета ограниченных диапазонов известен как «Случай Торндайка 2» — формула, разработанная психометристом Робертом Л. Торндайком.

Эта формула дает оценку истинной корреляции между двумя переменными и использует следующий расчет:

Истинная корреляция = √(1-(SD ² _{y ограничено} -SD ² _{y неограниченно} )) * (1-r ² _{ограничено} )

Золото:

• SD ² _{ограничено y} : квадрат стандартного отклонения доступных данных по переменной отклика y.
• _{Неограниченное} стандартное отклонение ² y: известный квадрат стандартного отклонения переменной ответа для совокупности.
• r ² _{ограничено} : квадратичная корреляция доступных ограниченных данных.

Было показано, что эта формула эффективна для получения несмещенных оценок истинной корреляции между двумя переменными, когда одна из переменных находится в ограниченном диапазоне.

Обратите внимание: чтобы использовать эту формулу, вам необходимо иметь оценку истинного стандартного отклонения генеральной совокупности для переменной ответа.