Что такое одномерный анализ? (определение & #038; пример)
Термин одномерный анализ относится к анализу одной переменной. Вы можете это запомнить, потому что приставка «уни» означает «один».
Цель одномерного анализа — понять распределение значений одной переменной. Вы можете сравнить этот тип анализа со следующим:
- Двумерный анализ : анализ двух переменных.
- Многомерный анализ: анализ двух или более переменных.
Например, предположим, что у нас есть следующий набор данных:
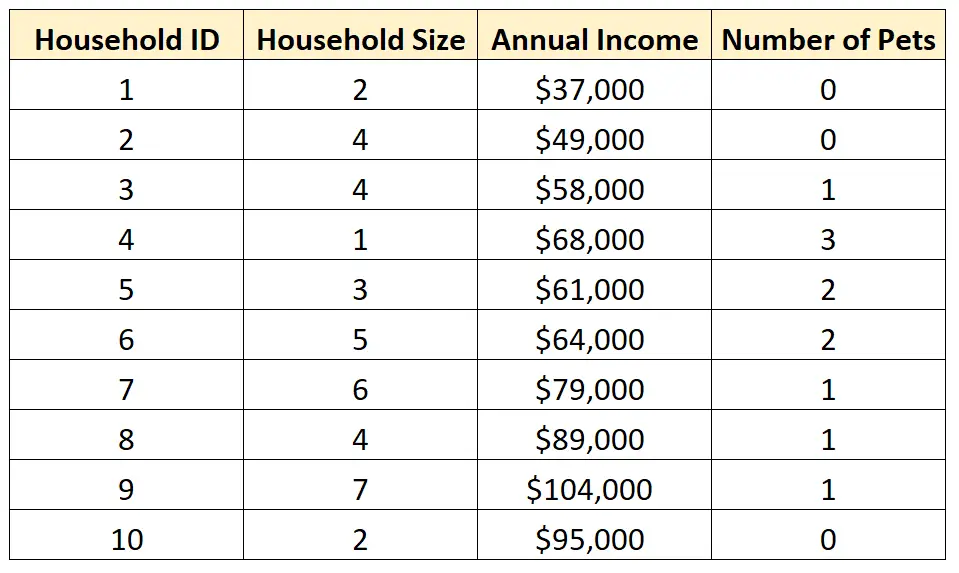
Мы могли бы решить провести одномерный анализ одной из отдельных переменных в наборе данных, чтобы лучше понять распределение ее значений.
Например, мы можем выполнить одномерный анализ переменной «Размер домохозяйства» :
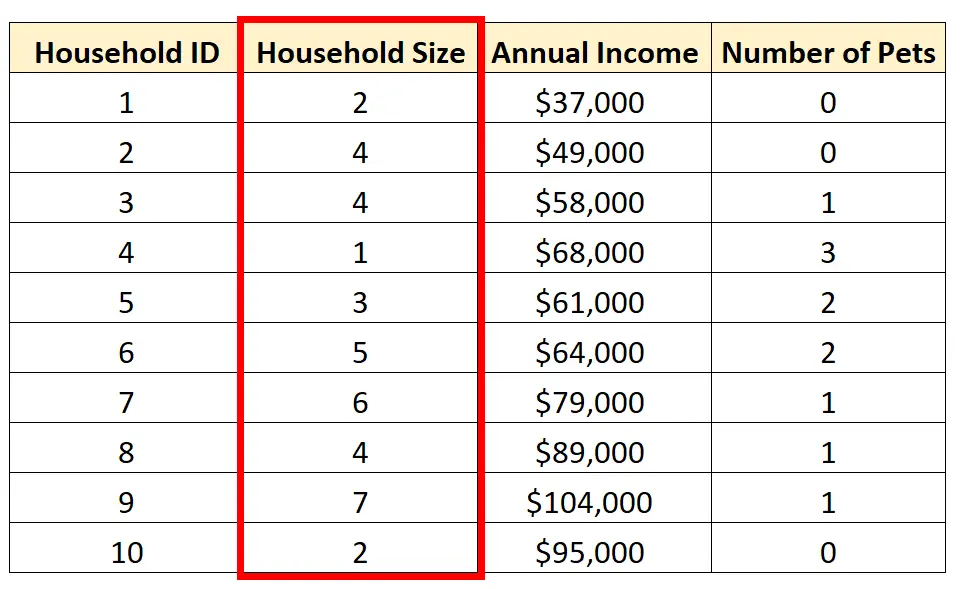
Существует три распространенных способа выполнения одномерного анализа:
1. Сводная статистика
Самый распространенный способ выполнения одномерного анализа — описать переменную с помощью сводной статистики .
Существует два распространенных типа сводной статистики:
- Меры центральной тенденции : эти числа описывают, где находится центр набора данных. Примеры включают среднее значение и медиану .
- Меры дисперсии : эти числа описывают распределение значений в наборе данных. Примеры включают интервал , межквартильный диапазон , стандартное отклонение и дисперсию .
2. Частотные распределения
Другой способ выполнить одномерный анализ — создать частотное распределение , которое описывает, как часто в наборе данных появляются разные значения.
3. Графика
Другой способ выполнения одномерного анализа — создание графиков для визуализации распределения значений определенной переменной.
Общие примеры включают в себя:
- Боксплоты
- Гистограммы
- Кривые плотности
- Камамберы
В следующих примерах показано, как выполнить каждый тип одномерного анализа с использованием переменной «Размер домохозяйства» из нашего ранее упомянутого набора данных:

Сводные статистические данные
Мы можем рассчитать следующие показатели центральной тенденции размера домохозяйства:
- Средний (среднее значение): 3,8
- Медиана (среднее значение): 4
Эти ценности дают нам представление о том, в чем заключается «центральная» ценность.
Мы также можем рассчитать следующие меры дисперсии:
- Диапазон (разница между максимумом и минимумом): 6
- Интерквартильная шкала (распределение средних 50% значений): 2,5
- Стандартное отклонение (средняя мера разброса): 1,87.
Эти значения дают нам представление о распределении значений этой переменной.
Распределение частоты
Мы также можем создать следующую таблицу распределения частот, чтобы суммировать, как часто встречаются разные значения:
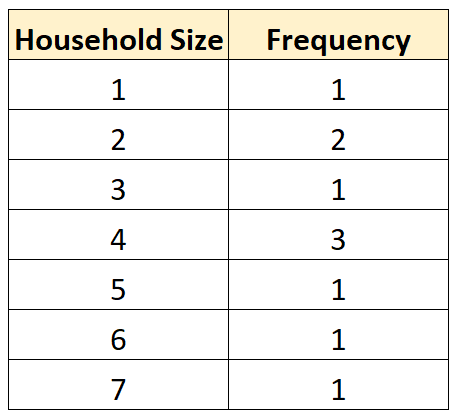
Это позволяет нам быстро увидеть, что наиболее распространенный размер домохозяйства составляет 4 человека .
Ресурс: вы можете использовать этот калькулятор частот для автоматического получения распределения частот для любой переменной.
Графика
Мы можем создать следующие графики, которые помогут нам визуализировать распределение значений размера домохозяйства:
1. Бокс-сюжет
Ящик — это график, показывающий пятизначную сводку набора данных.
Пятизначное резюме включает в себя:
- Минимальное значение
- Первый квартиль
- Медианное значение
- Третий квартиль
- Максимальное значение
Вот как будет выглядеть коробчатая диаграмма для переменной «Размер домохозяйства»:
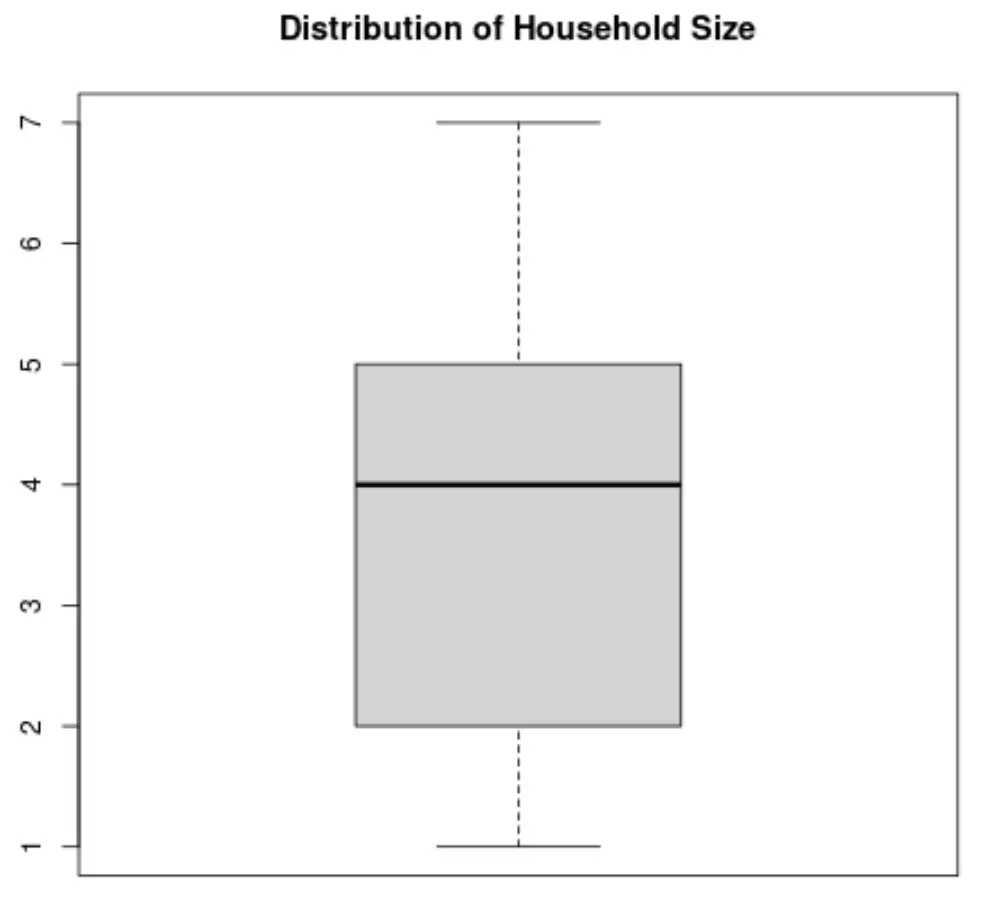
Ресурс: вы можете использовать этот генератор коробчатых диаграмм для автоматического создания коробчатой диаграммы для любой переменной.
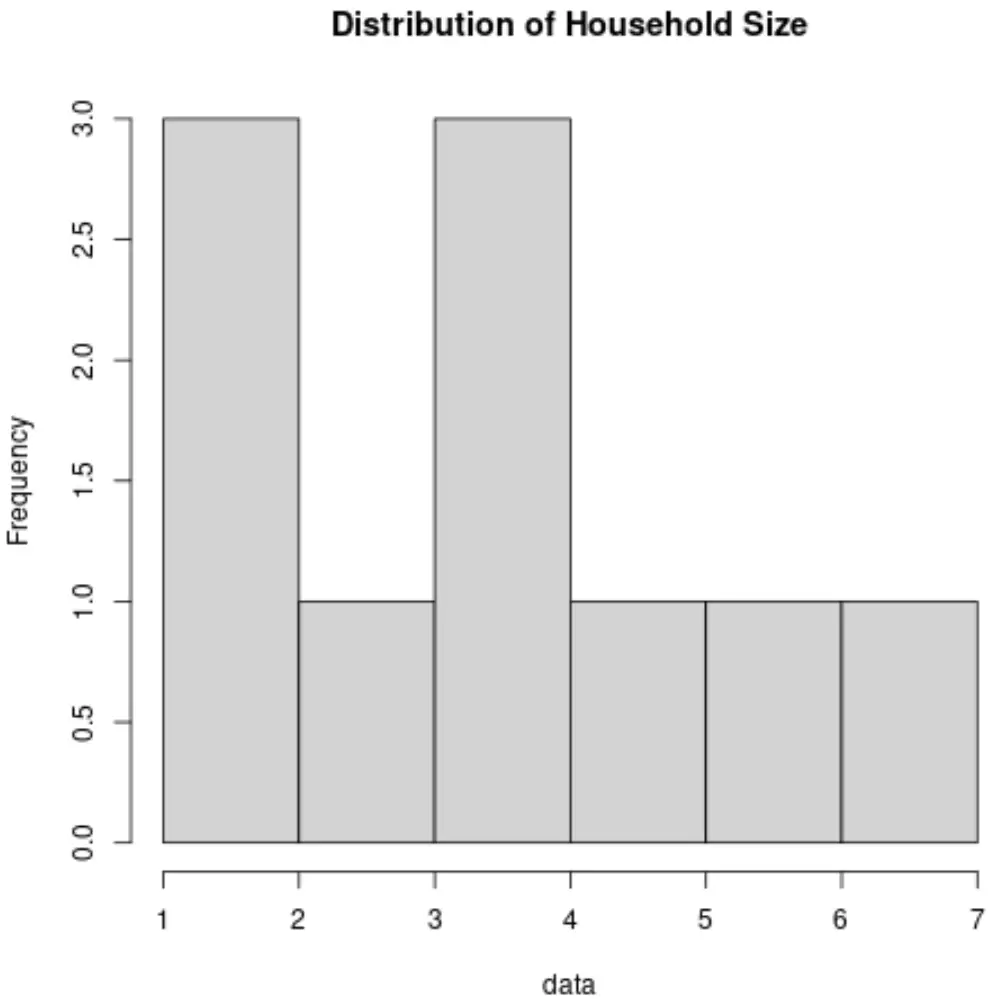
2. Гистограмма
Гистограмма — это тип диаграммы, в которой для отображения частот используются вертикальные полосы. Этот тип диаграммы — полезный способ визуализировать распределение значений в наборе данных.
Вот как будет выглядеть гистограмма для переменной «Размер домохозяйства»:
3. Кривая плотности
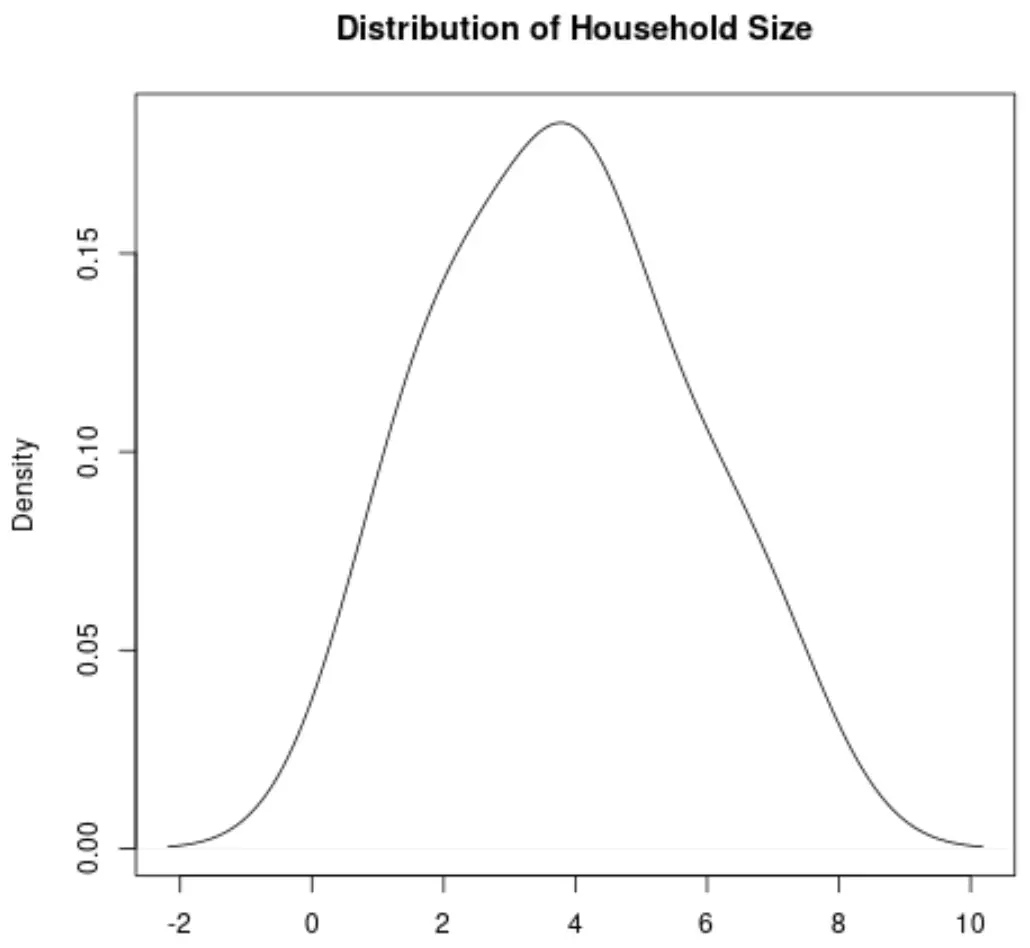
Кривая плотности — это кривая на графике, которая представляет распределение значений в наборе данных.
Это особенно полезно для визуализации «формы» распределения, в том числе того, имеет ли распределение один или несколько «пиков» частых значений и смещено ли распределение влево или вправо .
Вот как будет выглядеть кривая плотности переменной «Размер домохозяйства»:
4. Круговая диаграмма
Круговая диаграмма — это тип диаграммы в форме круга, в которой для представления пропорций целого используются фрагменты.
Вот как будет выглядеть круговая диаграмма для переменной «Размер домохозяйства»:
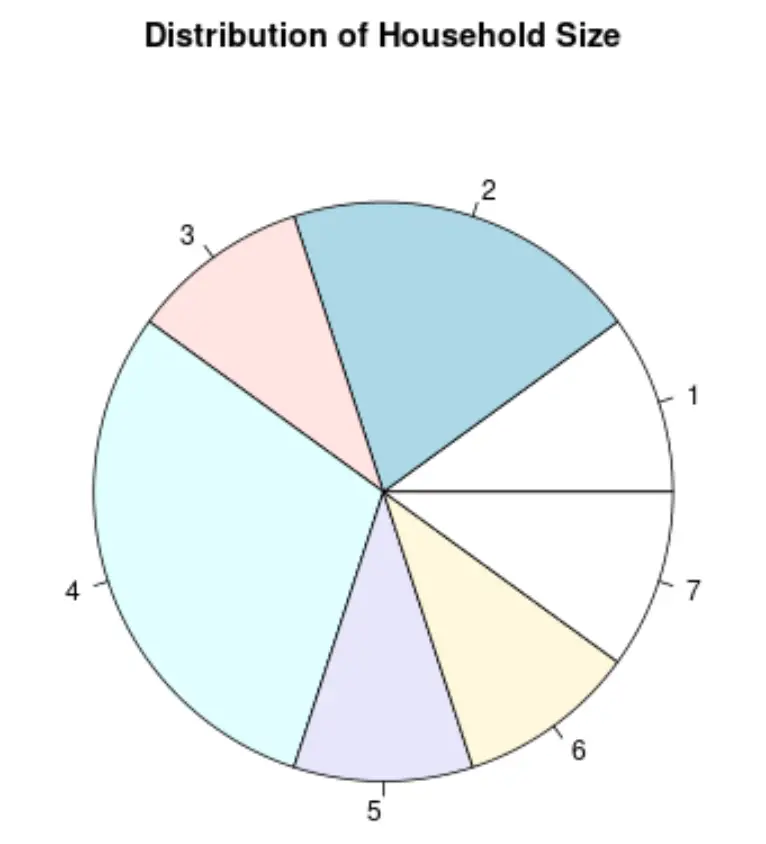
В зависимости от типа данных одна из этих диаграмм может оказаться более полезной для визуализации распределения значений, чем другие.