Как выполнить однофакторный дисперсионный анализ в stata

Однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.

Этот тип теста называется однофакторным дисперсионным анализом, поскольку мы анализируем влияние предикторной переменной на переменную отклика. Если бы нас вместо этого интересовало влияние двух переменных-предсказателей на переменную отклика, мы могли бы выполнить двусторонний дисперсионный анализ .

В этом руководстве объясняется, как выполнить однофакторный дисперсионный анализ в Stata.

Пример: односторонний дисперсионный анализ в Stata

В этом примере мы будем использовать встроенный набор данных Stata, называемый систолическим , для выполнения однофакторного дисперсионного анализа. Этот набор данных содержит следующие три переменные для 58 разных людей:

• Используемый препарат
• Болезнь пациента
• Изменение систолического артериального давления

Мы будем использовать следующие шаги, чтобы выполнить однофакторный дисперсионный анализ, чтобы определить, оказывает ли тип используемого лекарства значительное влияние на изменение систолического артериального давления.

Шаг 1: Загрузите данные.

Сначала загрузите данные, введя систолическое значение webuse в командном поле и нажав Enter.

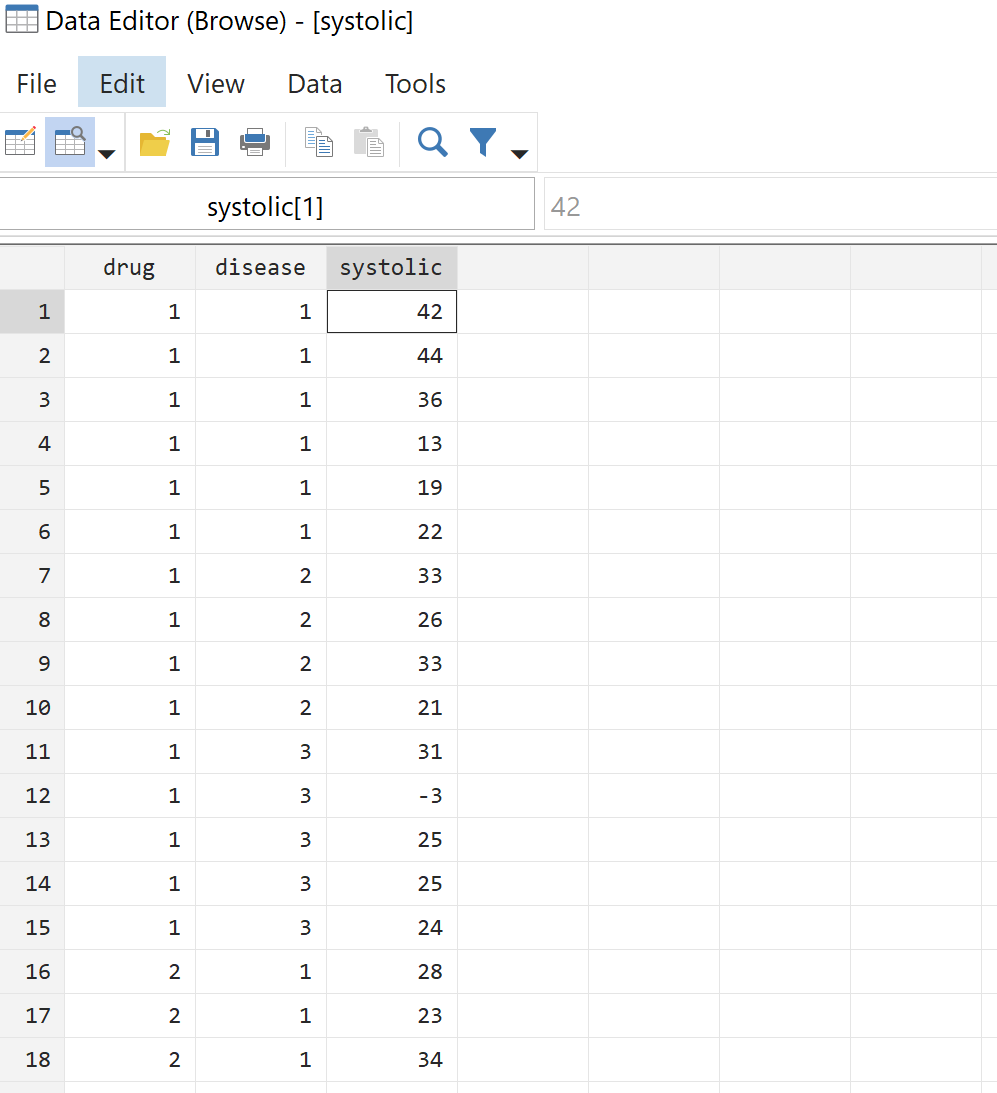
Шаг 2. Просмотрите необработанные данные.

Прежде чем выполнять однофакторный дисперсионный анализ, давайте сначала посмотрим на необработанные данные. В верхней строке меню выберите «Данные» > «Редактор данных» > «Редактор данных (Обзор)» . Это покажет нам фактические данные для всех 58 пациентов:

Шаг 3: Визуализируйте данные.

Далее давайте визуализируем данные. Мы создадим коробчатые диаграммы для отображения распределения значений систолического артериального давления для каждой категории лекарств.

В верхней строке меню выберите «Диаграммы» > «Ящики» . В разделе переменных выберите Систолическое:

Затем в подзаголовке «Категории» в разделе «Группирующая переменная» выберите препарат:

Нажмите ОК . Диаграмма с четырьмя коробчатыми диаграммами автоматически отобразится:

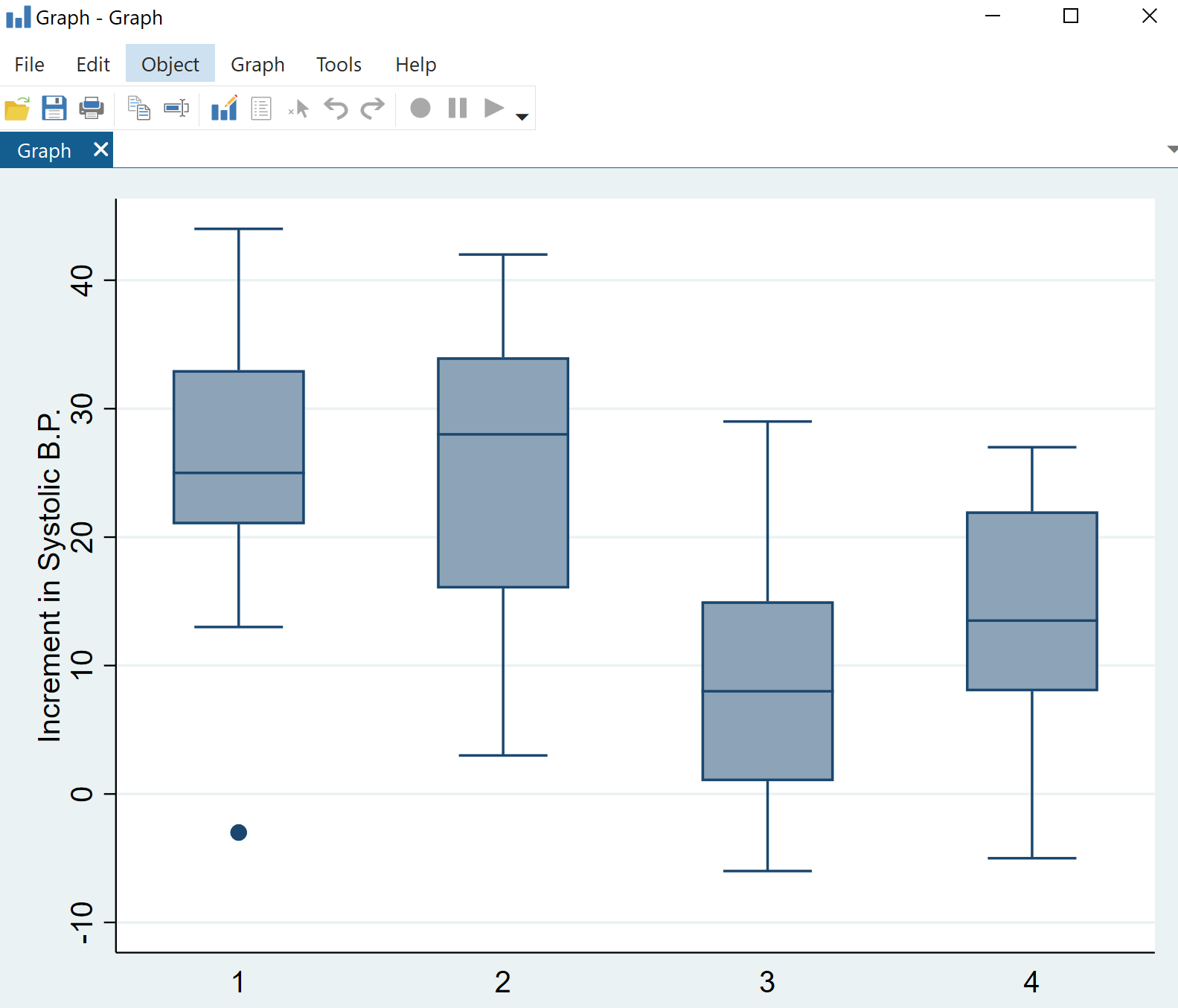
Мы сразу видим, что распределение изменений систолического артериального давления варьируется в зависимости от категории лекарств, но однофакторный дисперсионный анализ покажет нам, являются ли эти различия статистически значимыми.

Шаг 4: Выполните односторонний дисперсионный анализ.

В верхней строке меню перейдите к Статистика > Линейные и связанные модели > ANOVA/MANOVA > Однофакторный дисперсионный анализ .

В разделе «Переменная ответа» выберите «Систолическое». В рамках факторной переменной выберите препарат. Затем установите флажок рядом с надписью «Создать сводную таблицу» , чтобы мы могли увидеть базовую описательную статистику для каждой группы. Затем нажмите ОК .

Будет отображен следующий вывод:

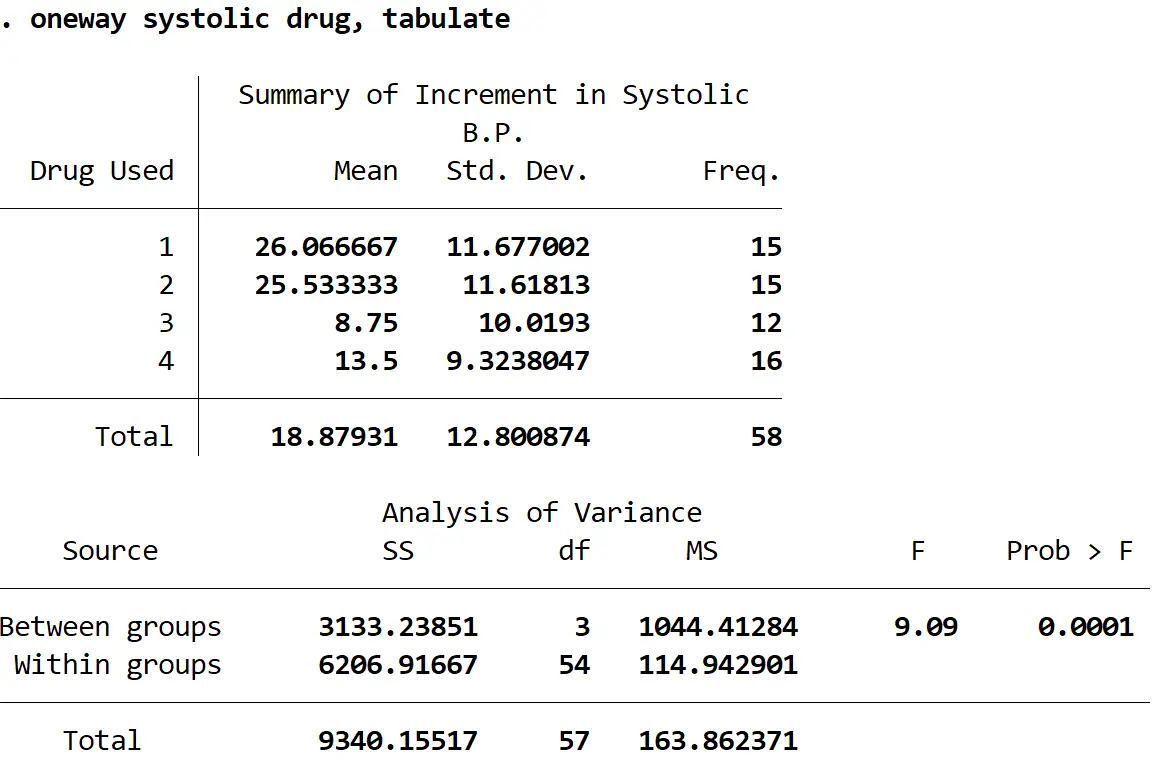
Статистика F равна 9,09 , а соответствующее значение p — 0,0001 . Поскольку значение p меньше альфа = 0,05, мы можем отвергнуть нулевую гипотезу о том, что среднее изменение систолического артериального давления для каждой группы одинаково.

Другими словами, существует статистически значимая разница в среднем изменении систолического артериального давления по крайней мере между двумя группами препаратов.

Шаг 5. Запустите несколько сравнительных тестов.

Затем мы можем запустить несколько сравнительных тестов, чтобы выяснить, какие средние группы отличаются друг от друга.

В верхней строке меню перейдите к «Статистика» > «Сводки, таблицы и тесты» > «Итоговая и описательная статистика» > «Парные сравнения средних» .

В качестве переменной выберите переменную систолического ответа. Для параметра «Более» выберите независимую переменную «наркотик» . Для корректировки для множественных сравнений выберите метод Тьюки .

Затем под подзаголовком «Отчетность» нажмите кнопку рядом с «Таблицы эффектов» и установите флажок «Показать таблицу эффектов с доверительными интервалами и p-значениями» . Затем нажмите ОК .

Будут отображены следующие результаты:

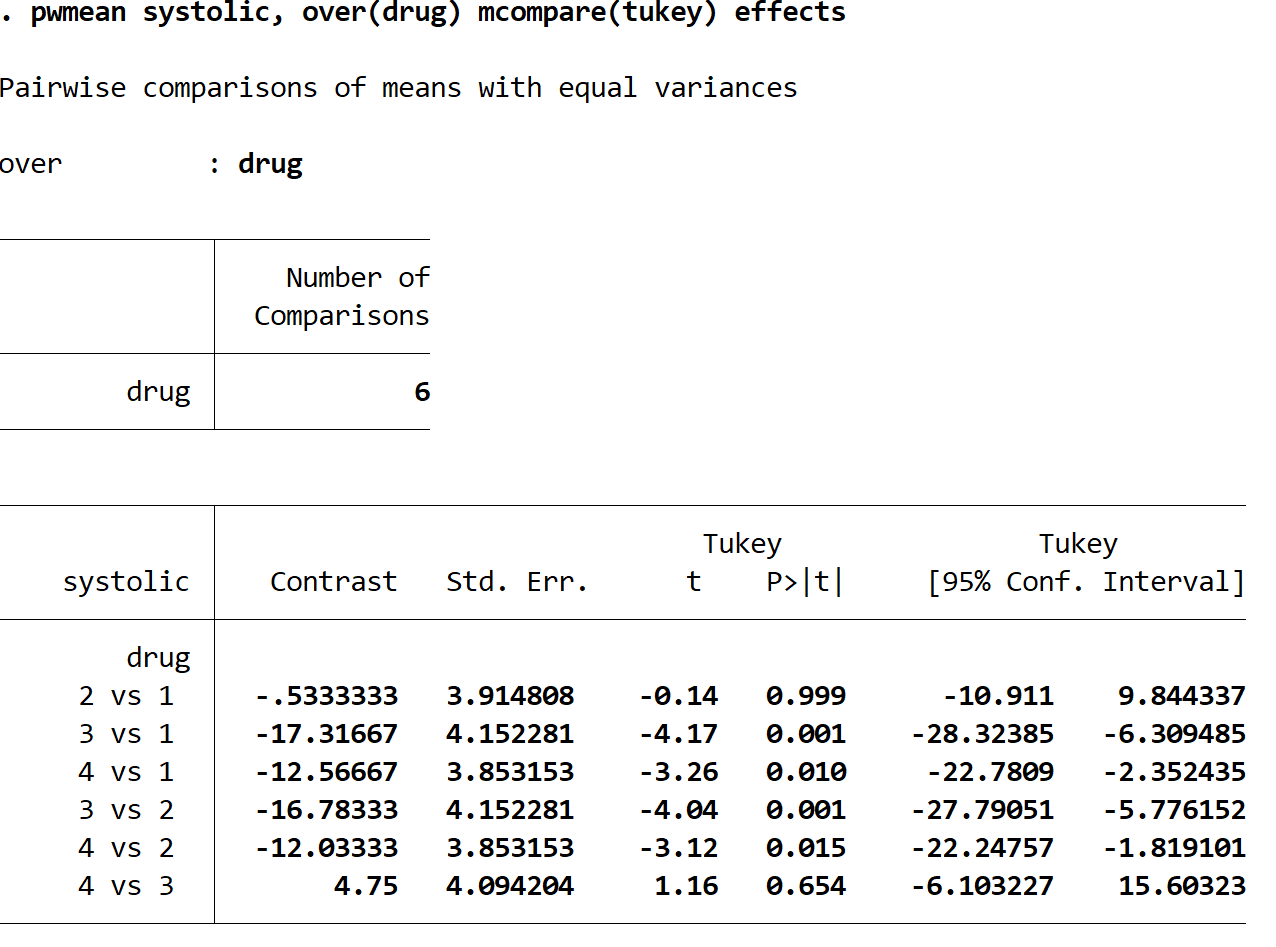
Каждая строка представляет собой сравнение двух конкретных групп препаратов. Например, в первой строке сравнивается среднее изменение систолического артериального давления между группой лекарств 2 и группой лекарств 1. Значение p для этого сравнения составляет 0,999 , что чрезвычайно высоко и не менее 0,05. Это означает, что статистически значимой разницы между группами препаратов 1 и 2 нет.

Однако мы видим, что значения p для следующих сравнений меньше 0,05:

• медицина 3 к 1 | р-значение = 0,001
• медицина 4 к 1 | p-значение = 0,010
• медицина 3 против 2 | р-значение = 0,001
• медицина 4 против 2 | р-значение = 0,015

Это означает, что разница в средних изменениях систолического артериального давления статистически значима между каждой из этих групп.

Шаг 6: Сообщите о результатах.

Наконец, мы сообщим о результатах нашего однофакторного анализа ANOVA. Вот пример того, как это сделать:

Был проведен однофакторный дисперсионный анализ, чтобы определить, оказывают ли четыре разных типа лекарств различное влияние на систолическое артериальное давление.

В следующей таблице суммировано количество участников в каждой группе, а также среднее изменение систолического артериального давления и стандартное отклонение систолического артериального давления для каждой группы:

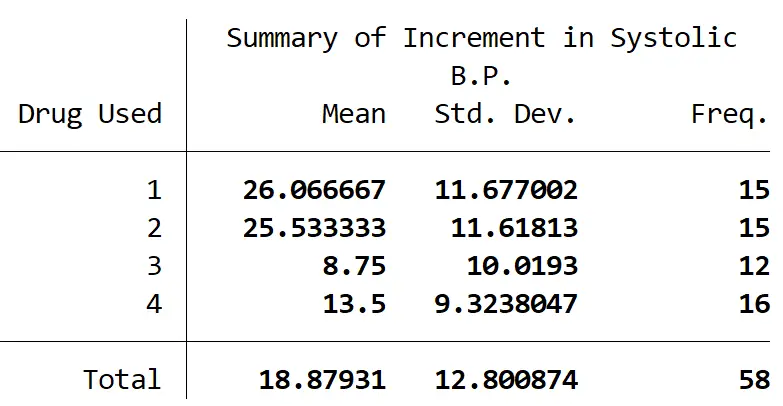
Однофакторный дисперсионный анализ показал, что существует статистически значимая разница как минимум между двумя группами (F(3, 54) = 9,09, p = 0,001).

Тест Тьюки для множественных сравнений выявил, что изменение систолического артериального давления было статистически значимо выше для препарата 3, чем для препарата 1 (17,32 +/- 4,15, р = 0,001), для препарата 3 по сравнению с препаратом 2 (16,78 +/- 4,15, р = 0,001), для препарата 4 по сравнению с препаратом 1 (12,57 +/- 3,85, р = 0,010) и для препарата 4 по сравнению с препаратом 2 (12,03 +/- 3,85, р = 0,015).

Не было статистически значимой разницы между группами препаратов 1 и 2 (0,533 +/- 3,91, р = 0,999) или между группами препаратов 3 и 4 (4,75 +/- 4,09, р = 0,654).