Как рассчитать коэффициент инфляции дисперсии (vif) в sas

В регрессионном анализе мультиколлинеарность возникает, когда две или более переменных-предикторов сильно коррелируют друг с другом, так что они не предоставляют уникальную или независимую информацию в модели регрессии.

Если степень корреляции между переменными достаточно высока, это может вызвать проблемы при подборе и интерпретации регрессионной модели.

Один из способов обнаружить мультиколлинеарность — использовать показатель, известный как коэффициент инфляции дисперсии (VIF) , который измеряет корреляцию и силу корреляции между объясняющими переменными в регрессионной модели .

В этом руководстве объясняется, как рассчитать VIF в SAS.

Пример: расчет VIF в SAS

В этом примере мы создадим набор данных, описывающий атрибуты 10 баскетболистов:

 /*create dataset*/
data my_data;
    input rating points assists rebounds;
    datalines ;
90 25 5 11
85 20 7 8
82 14 7 10
88 16 8 6
94 27 5 6
90 20 7 9
76 12 6 6
75 15 9 10
87 14 9 10
86 19 5 7
;
run ;

/*view dataset*/
proc print data =my_data; 

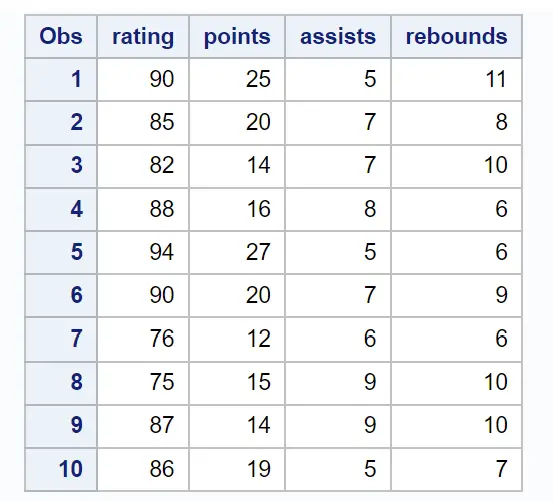
Допустим, мы хотим подогнать модель множественной линейной регрессии, используя оценку в качестве переменной ответа, а очки , передачи и подборы в качестве переменных-предсказателей.

Мы можем использовать PROC REG , чтобы согласовать эту модель регрессии с опцией VIF для расчета значений VIF для каждой предикторной переменной в модели:

 /*fit regression model and calculate VIF values*/
proc reg data =my_data;
    model rating = points assists rebounds / lively ;
run ; 

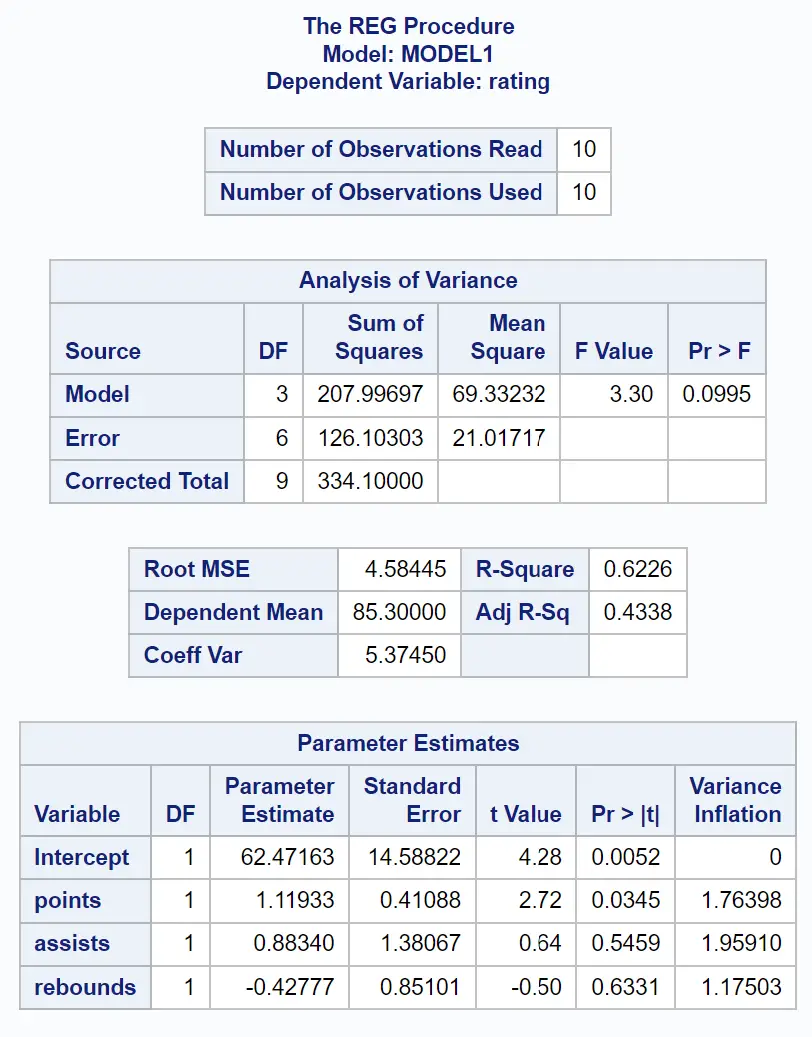
В таблице «Оценки параметров» мы можем увидеть значения VIF для каждой из переменных-предикторов:

• баллы: 1,76398
• передачи: 1,96591
• подборы: 1,17503

Примечание. Не обращайте внимания на VIF для «Перехвата» в шаблоне, поскольку это значение не имеет значения.

Значение VIF начинается с 1 и не имеет верхнего предела. Общее правило интерпретации VIF следующее:

• Значение 1 указывает на отсутствие корреляции между данной переменной-предиктором и любой другой переменной-предиктором в модели.
• Значение от 1 до 5 указывает на умеренную корреляцию между данной переменной-предиктором и другими переменными-предикторами в модели, но часто она недостаточно серьезна, чтобы требовать особого внимания.
• Значение больше 5 указывает на потенциально серьезную корреляцию между данной переменной-предиктором и другими переменными-предикторами в модели. В этом случае оценки коэффициентов и значения p в результатах регрессии, скорее всего, ненадежны.

Поскольку каждое из значений VIF переменных-предикторов в нашей регрессионной модели близко к 1, мультиколлинеарность не является проблемой в нашем примере.

Как бороться с мультиколлинеарностью

Если вы определите, что мультиколлинеарность является проблемой в вашей регрессионной модели, существует несколько распространенных способов ее решения:

1. Удалите одну или несколько сильно коррелирующих переменных.

В большинстве случаев это самое быстрое решение, и зачастую оно является приемлемым решением, поскольку удаляемые вами переменные в любом случае являются избыточными и добавляют в модель мало уникальной или независимой информации.

2. Линейно комбинирует переменные-предикторы каким-либо образом, например, каким-либо образом добавляя или вычитая их.

Сделав это, вы можете создать новую переменную, которая будет включать в себя информацию из обеих переменных, и у вас больше не возникнет проблема мультиколлинеарности.

3. Выполните анализ, предназначенный для учета сильно коррелирующих переменных, например, анализ главных компонент или регрессию частичных наименьших квадратов (PLS).

Эти методы специально разработаны для обработки сильно коррелированных переменных-предикторов.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в SAS:

Как выполнить множественную линейную регрессию в SAS
Как создать остаточный график в SAS
Как рассчитать расстояние приготовления в SAS