Как рассчитать ожидаемое значение x^2
Для случайной величины , обозначенной X, вы можете использовать следующую формулу для расчета ожидаемого значения X 2 :
E(X 2 ) = Σx 2 * p(x)
Золото:
- Σ : Символ, означающий «сумма».
- x : значение случайной величины
- p(x) : вероятность того, что случайная величина примет заданное значение.
Следующий пример показывает, как использовать эту формулу на практике.
Пример: Расчет ожидаемого значения X 2
Предположим, у нас есть следующая таблица распределения вероятностей, которая описывает вероятность того, что случайная величина:
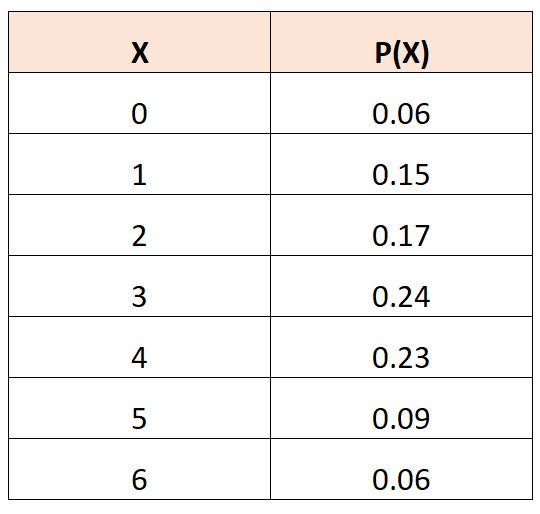
Чтобы рассчитать ожидаемое значение X 2 , мы можем использовать следующую формулу:
E(X 2 ) = Σx 2 * p(x)
E(X 2 ) = (0) 2 *.06 + (1) 2 *.15 + (2) 2 *.17 + (3) 2 *.24 + (4) 2 *.23 + (5) 2 *.09 + (6) 2 *.06
Е(Х 2 ) = 0 + 0,15 + 0,68 + 2,16 + 3,68 + 2,25+ 2,16
Е( Х2 ) = 11,08
Ожидаемое значение X 2 составляет 11,08 .
Обратите внимание, что эта случайная величина является дискретной случайной величиной , то есть она может принимать только конечное число значений.
Если X является непрерывной случайной величиной , мы должны использовать следующую формулу для расчета ожидаемого значения X 2 :
E(X 2 ) = ∫ x 2 f(x)dx
Золото:
- ∫: Символ, означающий «интеграция».
- f(x) : PDF-файл продолжается для случайной величины.
При расчете ожидаемого значения X2 для непрерывной случайной величины мы обычно используем статистическое программное обеспечение, поскольку этот расчет может быть сложнее выполнить вручную.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в статистике:
Как найти среднее значение распределения вероятностей
Как найти стандартное отклонение распределения вероятностей
Как найти дисперсию распределения вероятностей