Описательная или инференциальная статистика: в чем разница?

В области статистики существуют две основные отрасли:

• Описательная статистика
• Выведенный статистика

В этом руководстве объясняется разница между двумя ветвями и почему каждая из них полезна в определенных ситуациях.

Описательная статистика

Короче говоря, описательная статистика направлена на описание набора необработанных данных с использованием сводной статистики, графиков и таблиц.

Описательная статистика полезна, потому что она позволяет вам понять группу данных гораздо быстрее и проще, чем просто просматривать строки и строки значений необработанных данных.

Например, предположим, что у нас есть необработанный набор данных, показывающий результаты тестов 1000 учащихся конкретной школы. Нас может интересовать средний балл за тест, а также распределение результатов тестов.

Используя описательную статистику, мы смогли найти средний балл и построить график, который поможет нам визуализировать распределение баллов.

Это позволяет нам гораздо проще понять результаты тестов учащихся, чем просто просматривать необработанные данные.

Распространенные формы описательной статистики

Существует три распространенные формы описательной статистики:

1. Сводная статистика. Это статистика, которая суммирует данные с использованием одного числа. Существует два распространенных типа сводной статистики:

• Меры центральной тенденции : эти числа описывают, где находится центр набора данных. Примеры включают среднее   и медиана .
• Меры дисперсии: эти числа описывают распределение значений в наборе данных. Примеры включают интервал , межквартильный диапазон , стандартное отклонение и дисперсию .

2. Графика . Диаграммы помогают нам визуализировать данные. Распространенные типы диаграмм, используемые для визуализации данных, включают ящичковые диаграммы , гистограммы , диаграммы стеблей и листьев, а также диаграммы рассеяния .

3. Таблицы . Таблицы могут помочь нам понять, как распределяются данные. Распространенным типом таблицы является таблица частот , которая сообщает нам, сколько значений данных попадает в определенные диапазоны.

Пример использования описательной статистики

Следующий пример иллюстрирует, как мы можем использовать описательную статистику в реальном мире.

Предположим, что 1000 учеников определенной школы сдают один и тот же тест. Мы хотим понять распределение результатов тестов, поэтому используем следующую описательную статистику:

1. Сводная статистика

Средний: 82,13 . Это говорит нам о том, что средний балл теста среди 1000 студентов составляет 82,13.

Медиана: 84. Это говорит нам о том, что половина всех студентов набрала балл выше 84, а другая половина — ниже 84.

Макс.: 100. Мин.: 45. Это говорит нам о том, что максимальный балл, полученный любым учеником, составил 100, а минимальный балл — 45. Диапазон , который показывает нам разницу между максимальным и минимальным баллом, составляет 55.

2. Графика

Чтобы визуализировать распределение результатов тестирования, мы можем создать гистограмму — тип диаграммы, в которой для обозначения частот используются прямоугольные столбцы.

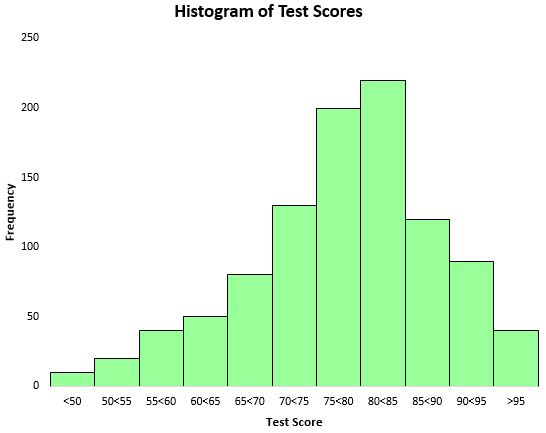
На основании этой гистограммы мы видим, что распределение результатов тестов имеет примерно колоколообразную форму. Большинство студентов набрали от 70 до 90 баллов, тогда как очень немногие набрали больше 95 и еще меньше баллов — ниже 50.

3. Таблицы

Еще один простой способ понять распределение оценок — создать таблицу частот. Например, в следующей таблице частот показан процент учащихся, набравших баллы между разными диапазонами:

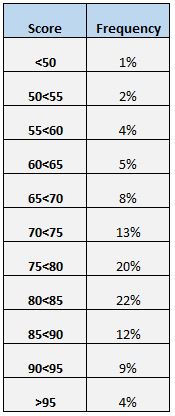
Мы видим, что только 4% от общего числа студентов набрали более 95 баллов. Мы также видим, что (12% + 9% + 4% =) 25% всех студентов набрали 85 или выше.

Таблица частот особенно полезна, если мы хотим знать, какой процент значений данных выше или ниже определенного значения. Например, предположим, что школа считает «приемлемым» результатом теста любой результат выше 75.

Глядя на таблицу частот, мы легко видим, что (20% + 22% + 12% + 9% + 4% = ) 67% студентов получили приемлемый балл по тесту.

Выведенный статистика

Короче говоря, инференциальная статистика использует небольшую выборку данных, чтобы сделать выводы о более крупной популяции, из которой формируется выборка.

Например, мы можем захотеть понять политические предпочтения миллионов людей в стране.

Однако опрос каждого человека в стране занял бы слишком много времени и денег. Поэтому вместо этого мы бы провели небольшой опрос, скажем, среди 1000 американцев, и использовали результаты опроса, чтобы сделать выводы о населении в целом.

В этом вся предпосылка статистики, основанной на выводах: мы хотим ответить на вопрос о совокупности, поэтому мы получаем данные для небольшой выборки этой совокупности и используем данные выборки, чтобы сделать выводы о совокупности.

Важность репрезентативной выборки

Чтобы быть уверенными в нашей способности использовать выборку для получения выводов о совокупности, мы должны убедиться, что у нас есть репрезентативная выборка , то есть выборка, в которой характеристики особей в популяции Выборка близко соответствует выборке. характеристики. от общей численности населения.

В идеале мы хотим, чтобы наша выборка напоминала «мини-версию» нашей популяции. Таким образом, если мы хотим сделать выводы о группе студентов, состоящей из 50% девочек и 50% мальчиков, наша выборка не была бы репрезентативной, если бы она включала 90% мальчиков и только 10% девочек.

Если наша выборка не похожа на генеральную совокупность в целом, мы не можем с уверенностью обобщить результаты выборки на генеральную совокупность в целом.

Как получить репрезентативную выборку

Чтобы максимизировать шансы на получение репрезентативной выборки, вам следует сосредоточиться на двух вещах:

1. Убедитесь, что вы используете метод случайной выборки.

Существует несколько методов случайной выборки, которые вы можете использовать, чтобы получить репрезентативную выборку, в том числе:

• Простая случайная выборка
• Систематическая случайная выборка
• Кластерная случайная выборка
• Стратифицированная случайная выборка

Методы случайной выборки, как правило, создают репрезентативные выборки, поскольку каждый член генеральной совокупности имеет равные шансы попасть в выборку.

2. Убедитесь, что размер вашей выборки достаточно велик .

Помимо использования соответствующего метода выборки, важно убедиться, что выборка достаточно велика, чтобы у вас было достаточно данных для обобщения на более широкую совокупность.

Чтобы определить размер выборки, вам необходимо учитывать размер изучаемой совокупности, уровень достоверности, который вы хотите использовать, и допустимую погрешность, которую вы считаете приемлемой.

К счастью, вы можете использовать онлайн-калькуляторы, чтобы ввести эти значения и посмотреть, каким должен быть размер вашей выборки.

Распространенные формы логической статистики

Существует три распространенные формы статистического вывода:

1. Проверка гипотез.

Мы часто хотим ответить на вопросы о группе населения, такие как:

• Процент людей в Огайо, поддерживающих кандидата А, превышает 50%?
• Средняя высота определенного растения равна 14 дюймам?
• Есть ли разница между средним ростом учеников в школе А и школе Б?

Чтобы ответить на эти вопросы, мы можем выполнить проверку гипотез , которая позволяет нам использовать данные выборки, чтобы сделать выводы о популяциях.

2. Доверительные интервалы .

Иногда мы хотим оценить определенное значение для популяции. Например, нас может интересовать средняя высота определенного вида растений в Австралии.

Вместо того, чтобы обходить и измерять каждое растение в стране, мы могли бы собрать небольшую выборку растений и измерить каждое из них. Затем мы можем использовать среднюю высоту растений в выборке для оценки средней высоты популяции.

Однако наша выборка вряд ли обеспечит точную оценку численности населения. К счастью, мы можем учесть эту неопределенность, создав доверительный интервал , который обеспечивает диапазон значений, в пределах которого мы уверены, что находится истинный параметр популяции.

Например, мы могли бы получить 95% доверительный интервал [13,2, 14,8], что означает, что мы на 95% уверены, что истинная средняя высота этого вида растений составляет от 13,2 до 14,8 дюймов.

3. Регрессия .

Иногда мы хотим понять взаимосвязь между двумя переменными в популяции.

Например, предположим, что мы хотим знать, связаны ли часы, потраченные на учебу в неделю, с результатами тестов . Чтобы ответить на этот вопрос, мы могли бы применить метод, известный как регрессионный анализ .

Итак, мы можем посмотреть на количество изученных часов, а также на результаты тестов 100 студентов и провести регрессионный анализ, чтобы увидеть, существует ли значимая связь между двумя переменными.

Если значение p регрессии окажется значимым , то мы можем заключить, что существует значительная связь между этими двумя переменными в общей численности студентов.

Разница между описательной и инференциальной статистикой

Подводя итог, разницу между описательной и индуктивной статистикой можно описать следующим образом:

Описательная статистика использует сводную статистику, графики и таблицы для описания набора данных.

Это полезно для того, чтобы помочь нам быстро и легко понять набор данных, не проходя через все отдельные значения данных.

Инференциальная статистика использует выборки, чтобы сделать выводы о более крупных популяциях.

В зависимости от вопроса о совокупности, на который вы хотите ответить, вы можете решить использовать один или несколько из следующих методов: проверка гипотез, доверительные интервалы и регрессионный анализ.

Если вы решите использовать один из этих методов, имейте в виду, что ваша выборка должна быть репрезентативной для вашей популяции , иначе сделанные вами выводы не будут надежными.