Как создать остаточный путь вручную
Остаточный график — это тип графика, который отображает значения переменной-предиктора в модели регрессии по оси X и значения остатков по оси Y.
Этот график используется для оценки того, нормально ли распределяются остатки регрессионной модели и проявляют ли они гетероскедастичность .
В следующем пошаговом примере показано, как вручную создать график остатков для регрессионной модели.
Шаг 1. Найдите прогнозируемые значения
Предположим, мы хотим подогнать модель регрессии к следующему набору данных:
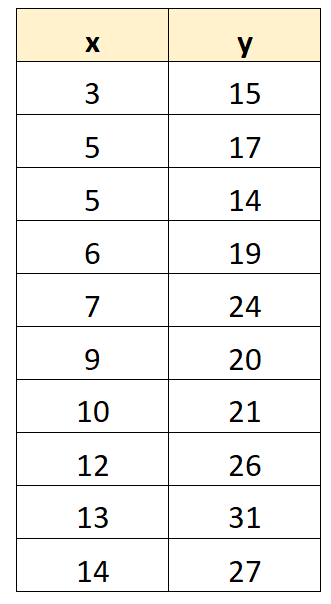
Используя статистическое программное обеспечение (например, Excel, R, Python, SPSS и т. д.), мы видим, что подобранная модель регрессии:
у = 10,4486 + 1,3037(х)
Затем мы можем использовать эту модель для прогнозирования значения y на основе значения x. Например, если x = 3, мы прогнозируем, что y будет:
у = 10,4486 + 1,3037(3) = 14,359
Мы можем повторить этот процесс для каждого наблюдения в нашем наборе данных:
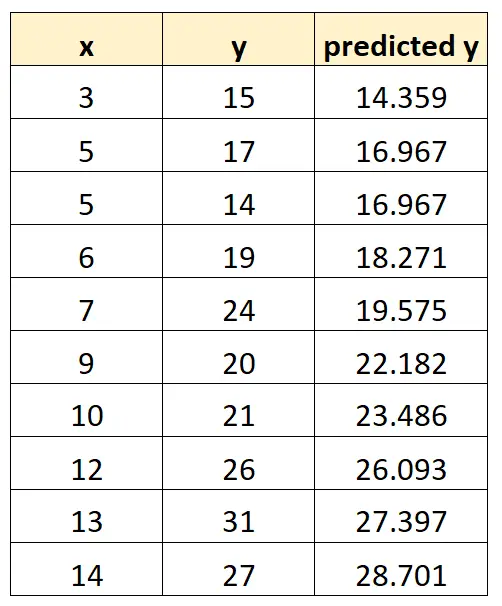
Шаг 2: Найдите остатки
Остаток для данного наблюдения в нашем наборе данных рассчитывается следующим образом:
Остаток = наблюдаемое значение – прогнозируемое значение
Например, остаток первого наблюдения будет рассчитываться следующим образом:
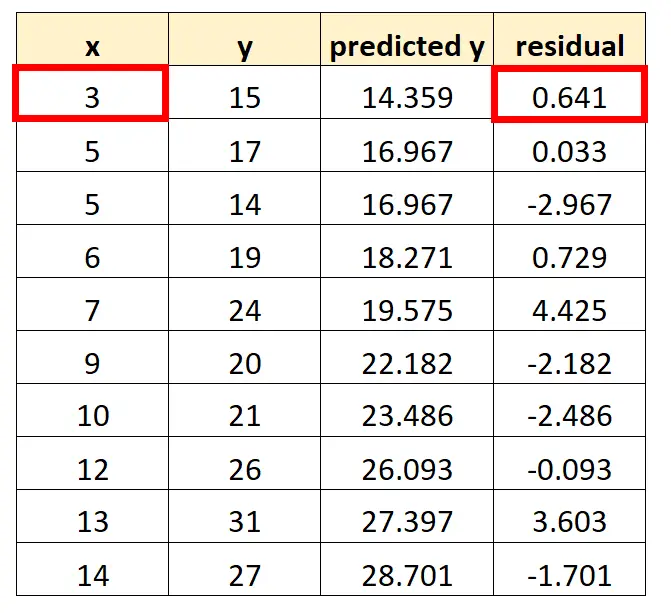
Остаток = 15 – 14,359 = 0,641
Мы можем повторить этот процесс для каждого наблюдения в нашем наборе данных:
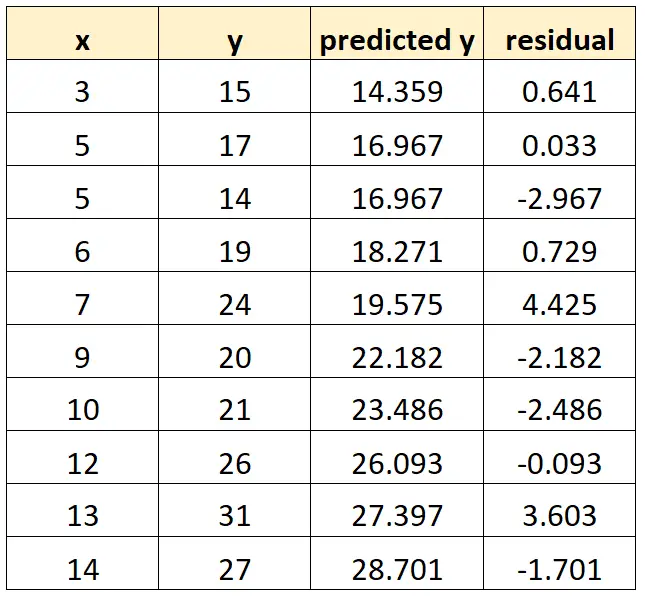
Шаг 3. Создайте остаточный график
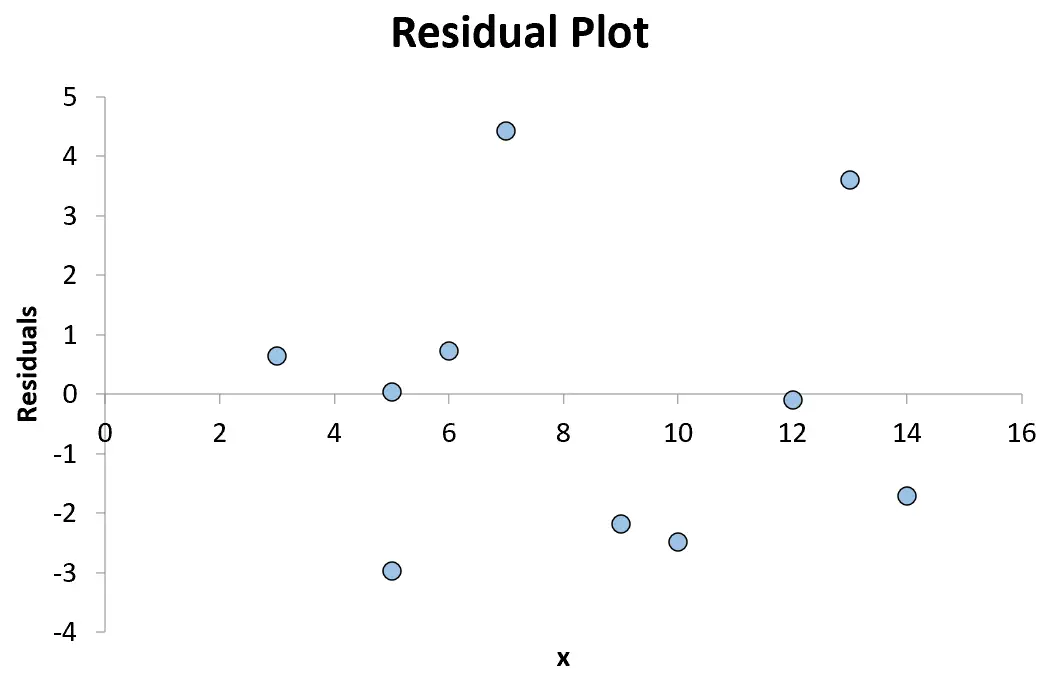
Наконец, мы можем создать график остатков, разместив значения x по оси x, а остатки — по оси y.
Например, первая точка, которую мы поместим на наш график, — это (3, 0,641).
Следующая точка, которую мы разместим на нашем графике, это (5, 0,033).
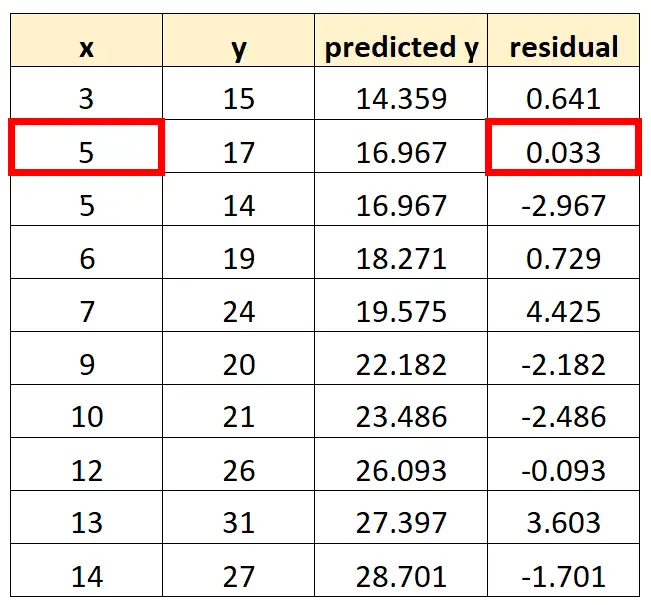
Мы продолжим до тех пор, пока не разместим на графике все 10 парных комбинаций значений x и остатков:

Любая точка выше нуля на графике представляет собой положительный остаток. Это означает, что наблюдаемое значение y больше, чем значение, предсказанное регрессионной моделью.
Любая точка меньше нуля представляет собой отрицательный остаток. Это означает, что наблюдаемое значение y ниже значения, предсказанного регрессионной моделью.
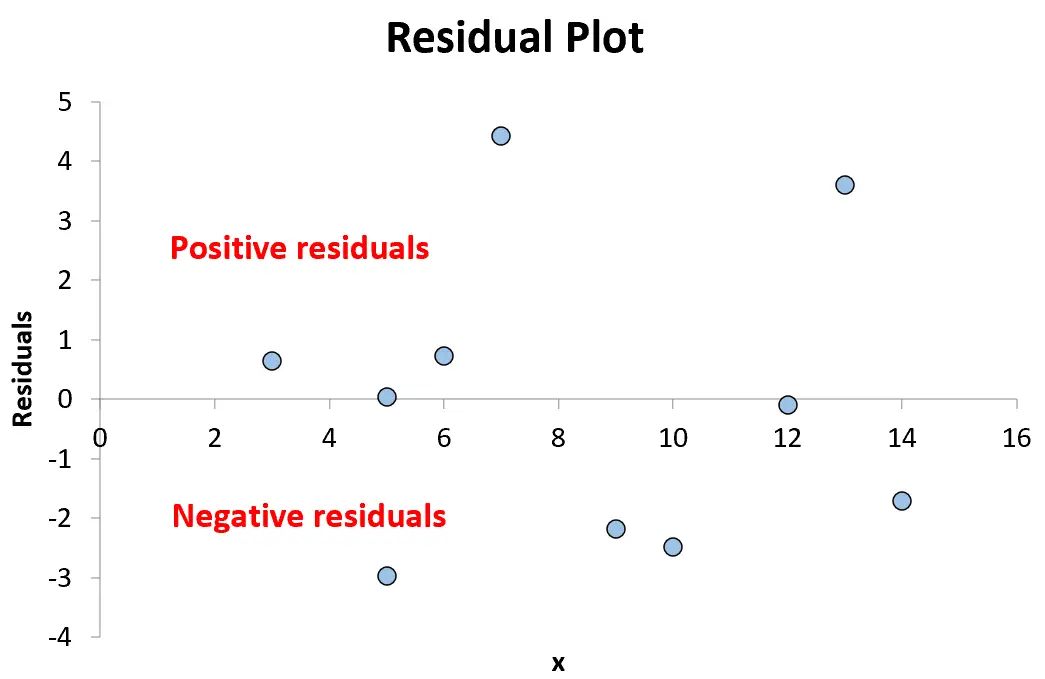
Поскольку точки на графике случайным образом разбросаны вокруг остатка 0 без четкой закономерности, это указывает на то, что связь между x и y является линейной и уместно использовать модель линейной регрессии.
А поскольку остатки не увеличиваются и не уменьшаются систематически по мере увеличения предикторной переменной, это означает, что гетероскедастичность не является проблемой для этой регрессионной модели.
Дополнительные ресурсы
В следующих руководствах объясняется, как создавать графики остатков с использованием различного статистического программного обеспечения:
Как создать график остатков на калькуляторе TI-84
Как создать остаточный график в Excel
Как создать остаточный график в R
Как создать остаточный график в Python