Как посчитать остаточную сумму квадратов в excel
Остаток — это разница между наблюдаемым значением и прогнозируемым значением в регрессионной модели.
Он рассчитывается следующим образом:
Остаток = Наблюдаемое значение – Прогнозируемое значение
Один из способов понять, насколько хорошо модель регрессии соответствует набору данных, — это вычислить остаточную сумму квадратов , которая рассчитывается следующим образом:
Остаточная сумма квадратов = Σ(e i ) 2
Золото:
- Σ : греческий символ, означающий «сумма».
- e i : i- й остаток
Чем ниже значение, тем лучше модель соответствует набору данных.
В этом руководстве представлены примеры расчета остаточной суммы квадратов для простой модели линейной регрессии и модели множественной линейной регрессии в Excel.
Пример 1: Остаточная сумма квадратов для простой линейной регрессии
Предположим, у нас есть следующий набор данных в Excel:
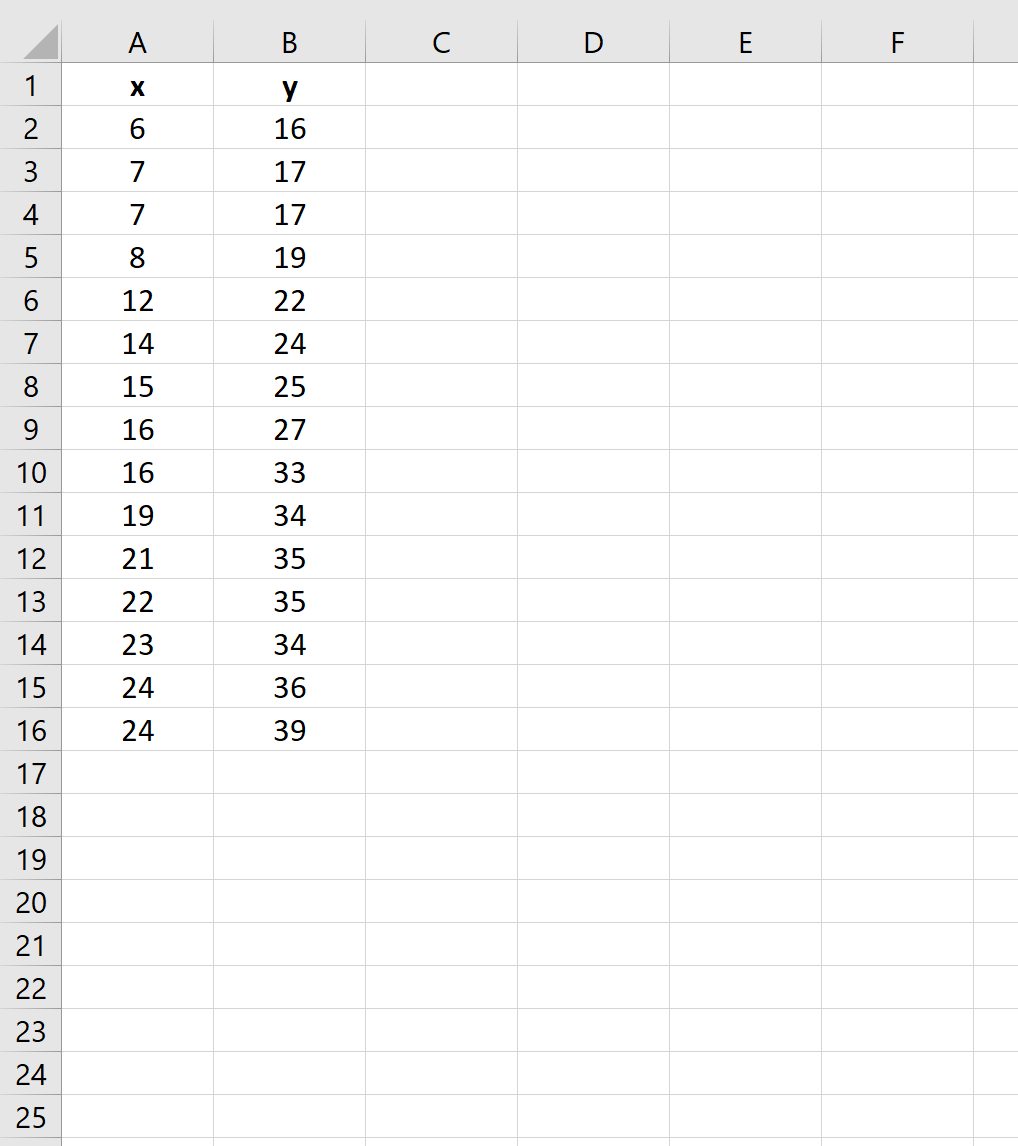
Чтобы вычислить остаточную сумму квадратов для простой модели линейной регрессии, используя x в качестве переменной-предиктора и y в качестве переменной ответа, мы можем использовать функцию ЛИНЕЙН() , которая использует следующий синтаксис:
ЛИНЕЙН(известный_ys, [известный_xs], [const], [статистика])
Золото:
- известные_ys: диапазон значений y
- known_sx: диапазон значений x.
- const: нужно ли приводить константу b к нулю. Мы оставим это поле пустым.
- статистика: список статистики регрессии. Уточним, что это ПРАВДА.
На следующем снимке экрана показано, как использовать эту функцию на практике:
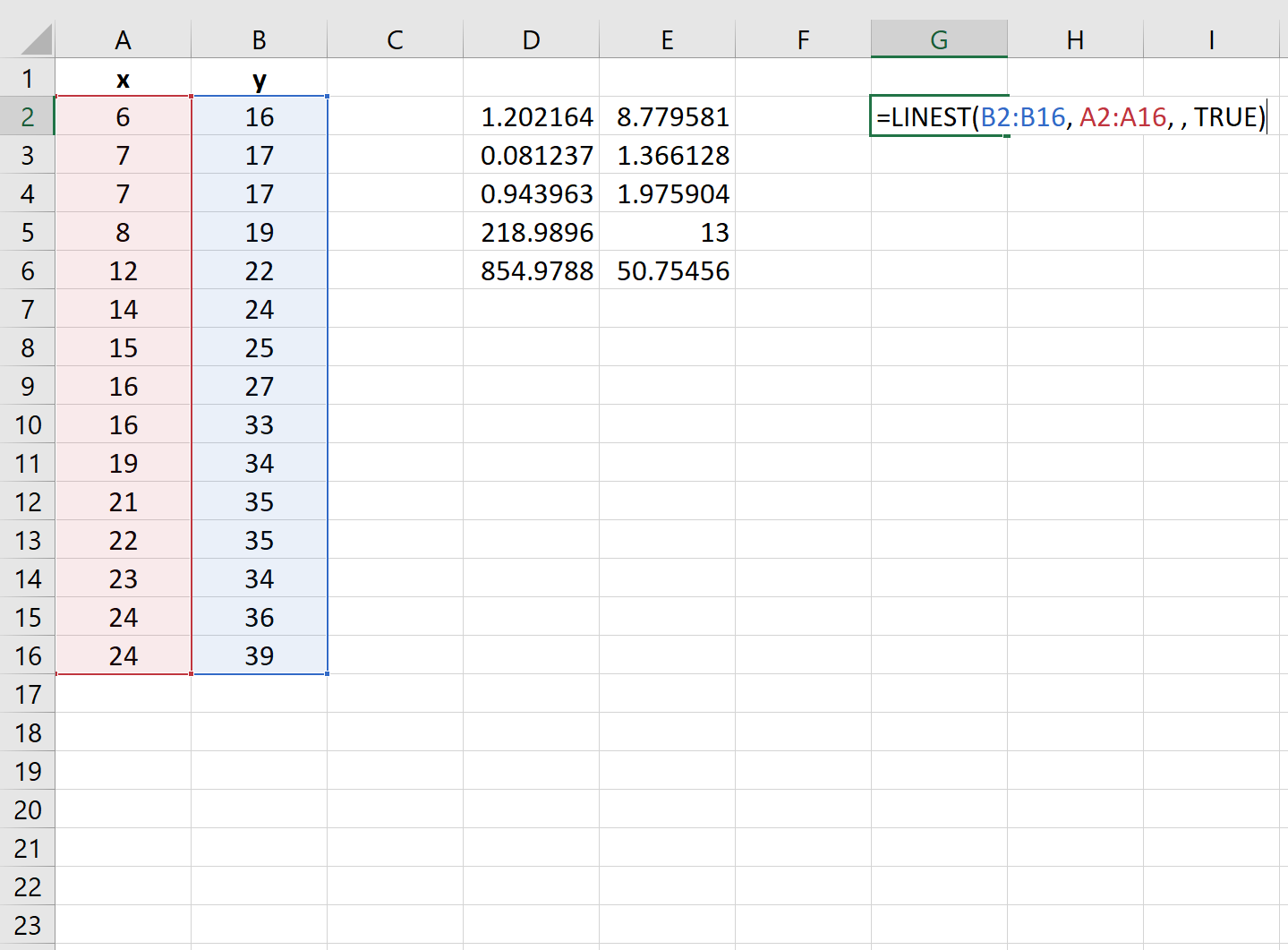
Остаточная сумма квадратов регрессионной модели отображается в последней ячейке второго столбца выходных данных. В этом примере остаточная сумма квадратов оказывается 50,75 .
Пример 2: Остаточная сумма квадратов для множественной линейной регрессии
Предположим, у нас есть следующий набор данных в Excel:
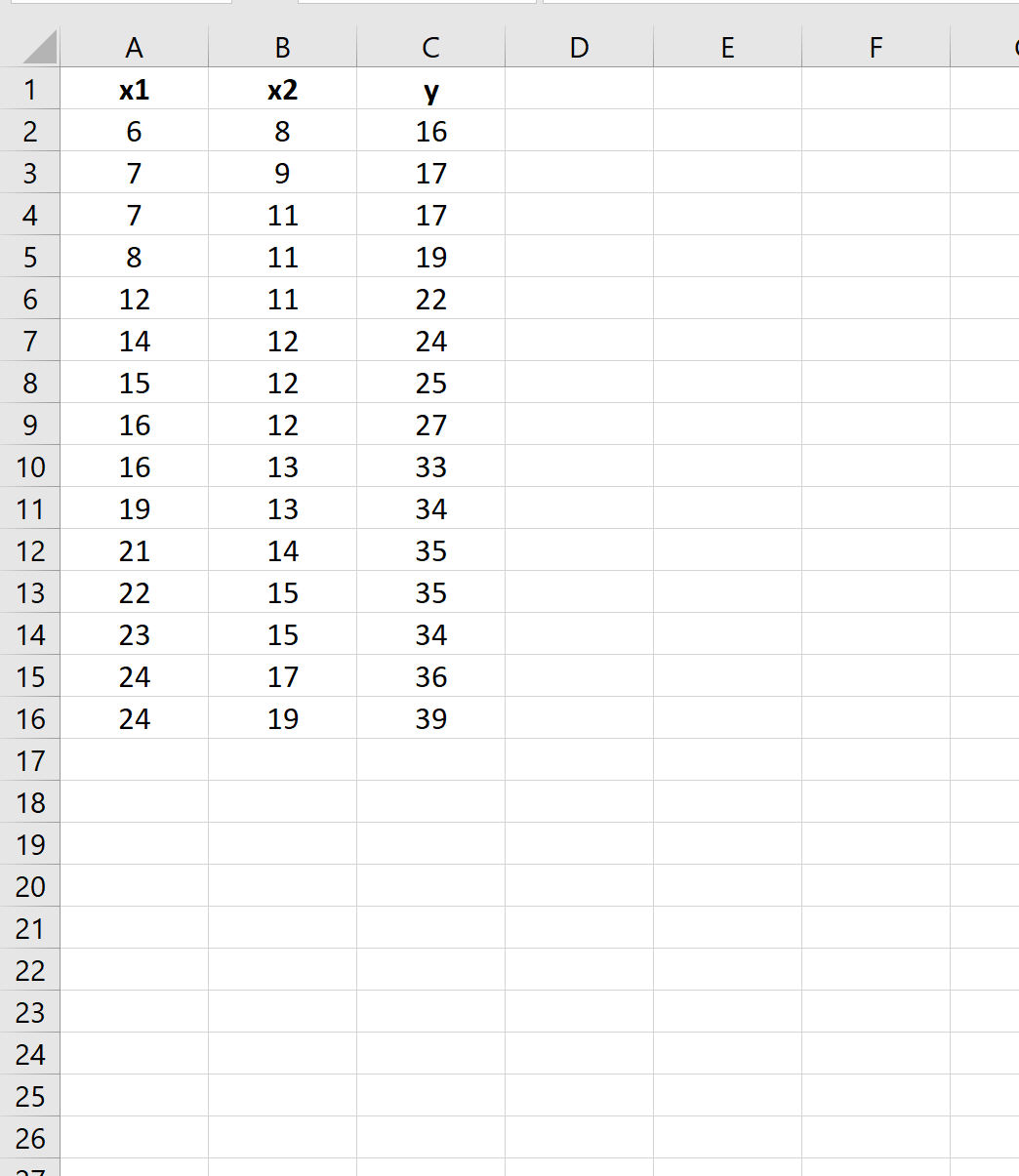
Опять же, мы можем использовать функцию ЛИНЕЙН() для расчета остаточной суммы квадратов модели.
Единственное отличие состоит в том, что мы укажем два столбца значений для аргументаknown_xs :
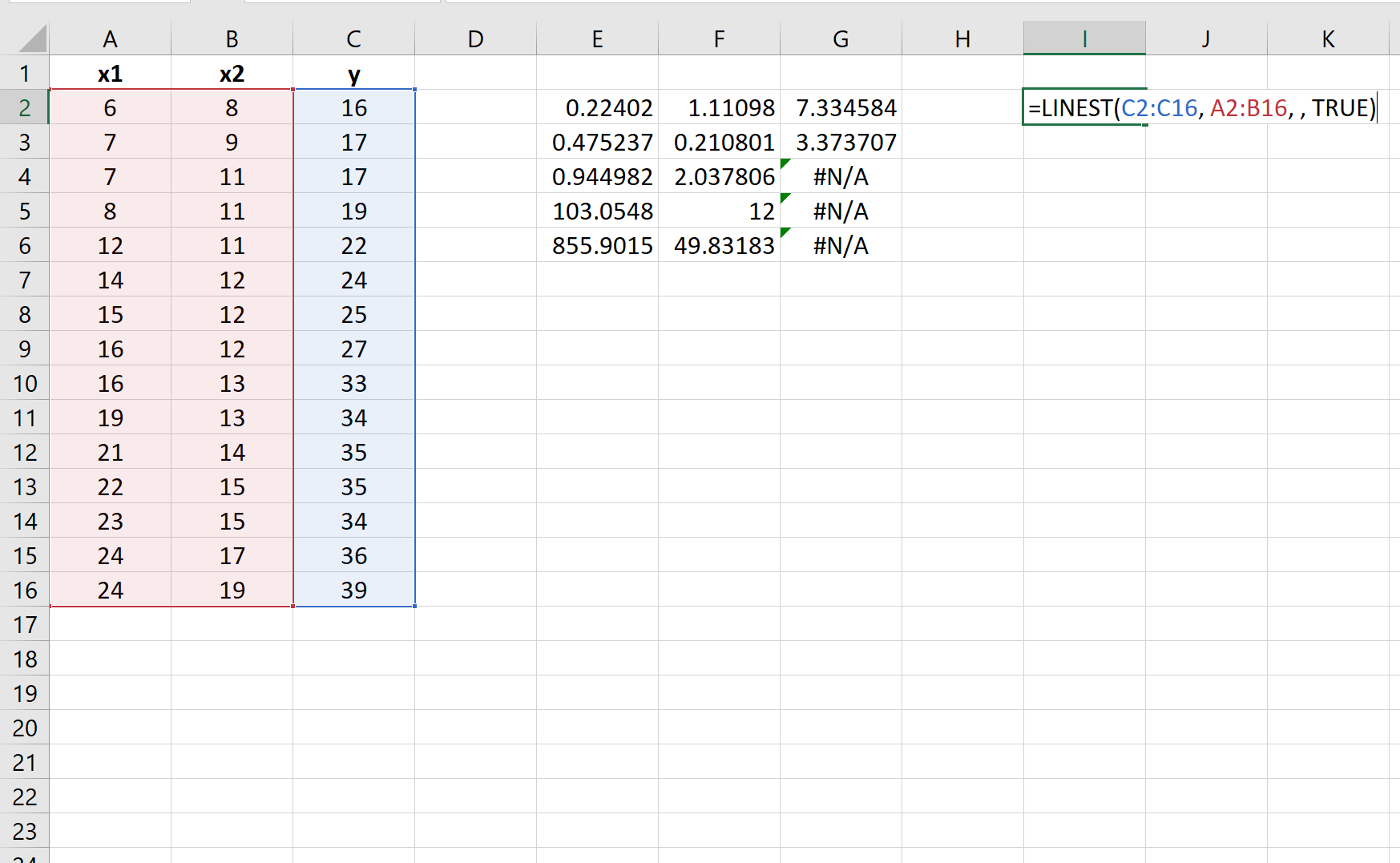
Остаточная сумма квадратов для этой модели множественной линейной регрессии равна 49,83 .
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Калькулятор остаточной суммы квадратов