Как найти дисперсию сгруппированных данных (с примером)

Мы часто хотим вычислить дисперсию сгруппированного распределения частот.

Например, предположим, что у нас есть следующее сгруппированное распределение частот:

Хотя вычислить точную дисперсию невозможно, поскольку мы не знаем исходных значений данных , дисперсию можно оценить, используя следующую формулу:

Дисперсия: Σn _i (m _i -μ) ² / (N-1)

Золото:

• n _i : Частота i- ^й группы
• _mi : Середина i- ^й группы.
• μ : Среднее значение
• N: общий размер выборки

Примечание. Середину каждой группы можно найти, взяв среднее значение нижнего и верхнего значений диапазона. Например, середина первой группы рассчитывается так: (1+10)/2 = 5,5.

Следующий пример показывает, как использовать эту формулу на практике.

Пример: вычисление дисперсии сгруппированных данных

Предположим, у нас есть следующие сгруппированные данные:

Вот как мы могли бы использовать формулу, упомянутую ранее, для расчета дисперсии этих сгруппированных данных:

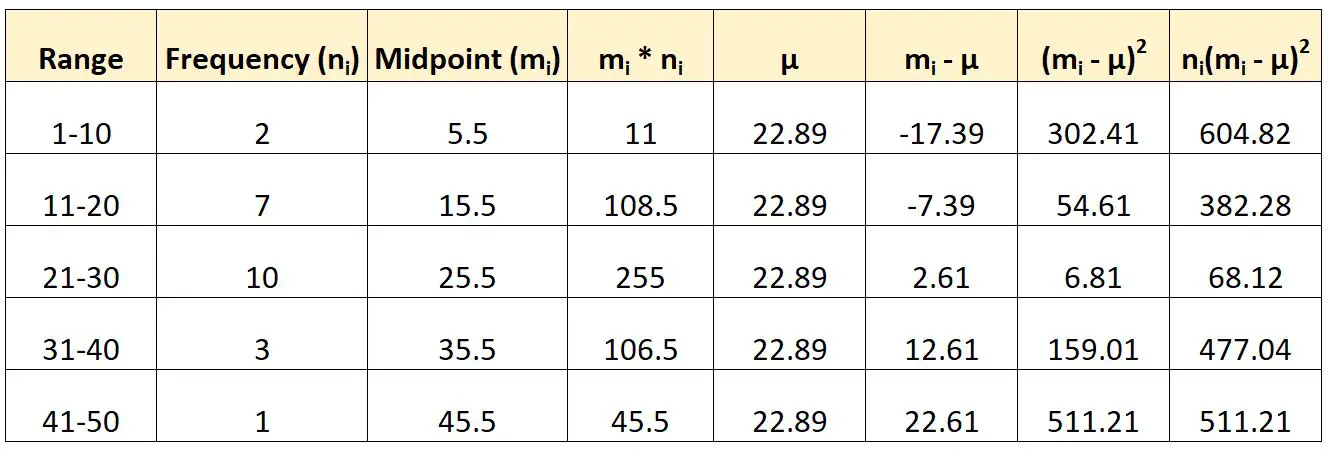
Затем мы рассчитаем дисперсию следующим образом:

• Дисперсия: Σn _i (m _i -μ) ² / (N-1)
• Разница : (604,82 + 382,28 + 68,12 + 477,04 + 511,21) / (23-1)
• Разница : 92,885

Дисперсия набора данных оказывается равной 92,885 .

Дополнительные ресурсы

В следующих руководствах объясняется, как рассчитать другие метрики для сгруппированных данных:

Как найти среднее и стандартное отклонение сгруппированных данных
Как рассчитать процентильный рейтинг для сгруппированных данных
Как найти медиану сгруппированных данных
Как найти режим сгруппированных данных