Как рассчитать средний диапазон в excel
Средний диапазон набора данных рассчитывается как:
Средний диапазон = (наибольшее значение + наименьшее значение) / 2
Это значение представляет собой просто среднее арифметического наибольшего и наименьшего значений в наборе данных и дает нам представление о том, где находится центр набора данных.
В этом руководстве объясняется, как рассчитать средний диапазон набора данных в Excel.
Пример: расчет среднего диапазона в Excel
Предположим, у нас есть следующий набор данных в Excel:
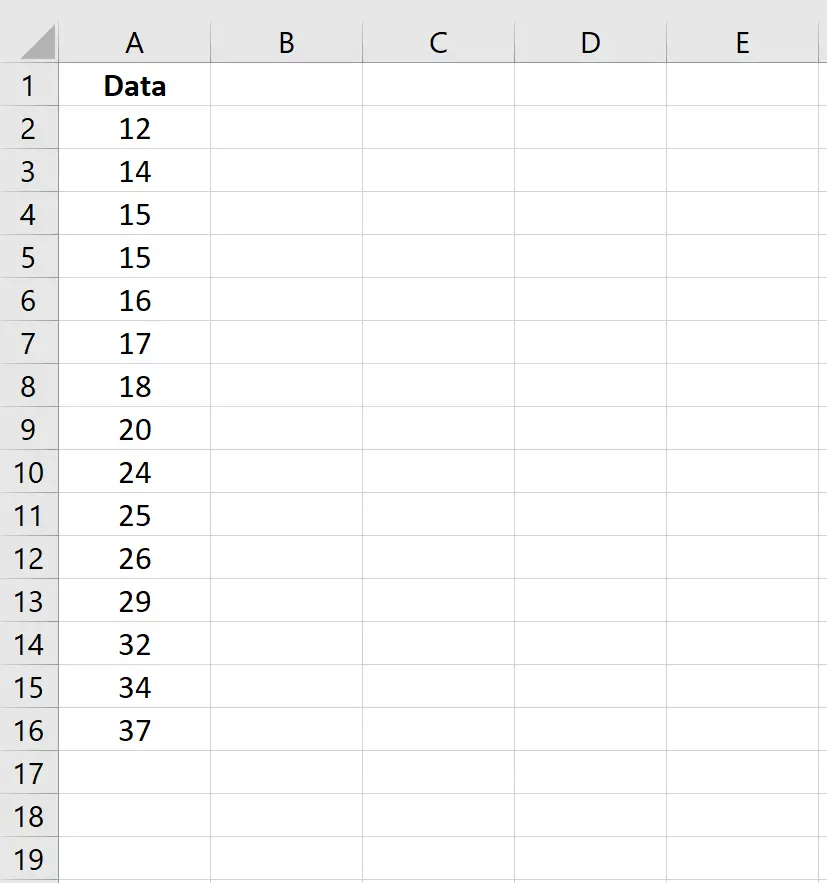
Для расчета среды мы можем использовать простую формулу:
=(MAX(диапазон значений) + MIN(диапазон значений)) / 2
В столбце D показан средний диапазон нашего набора данных, а в столбце E показана формула, которую мы использовали для его расчета:
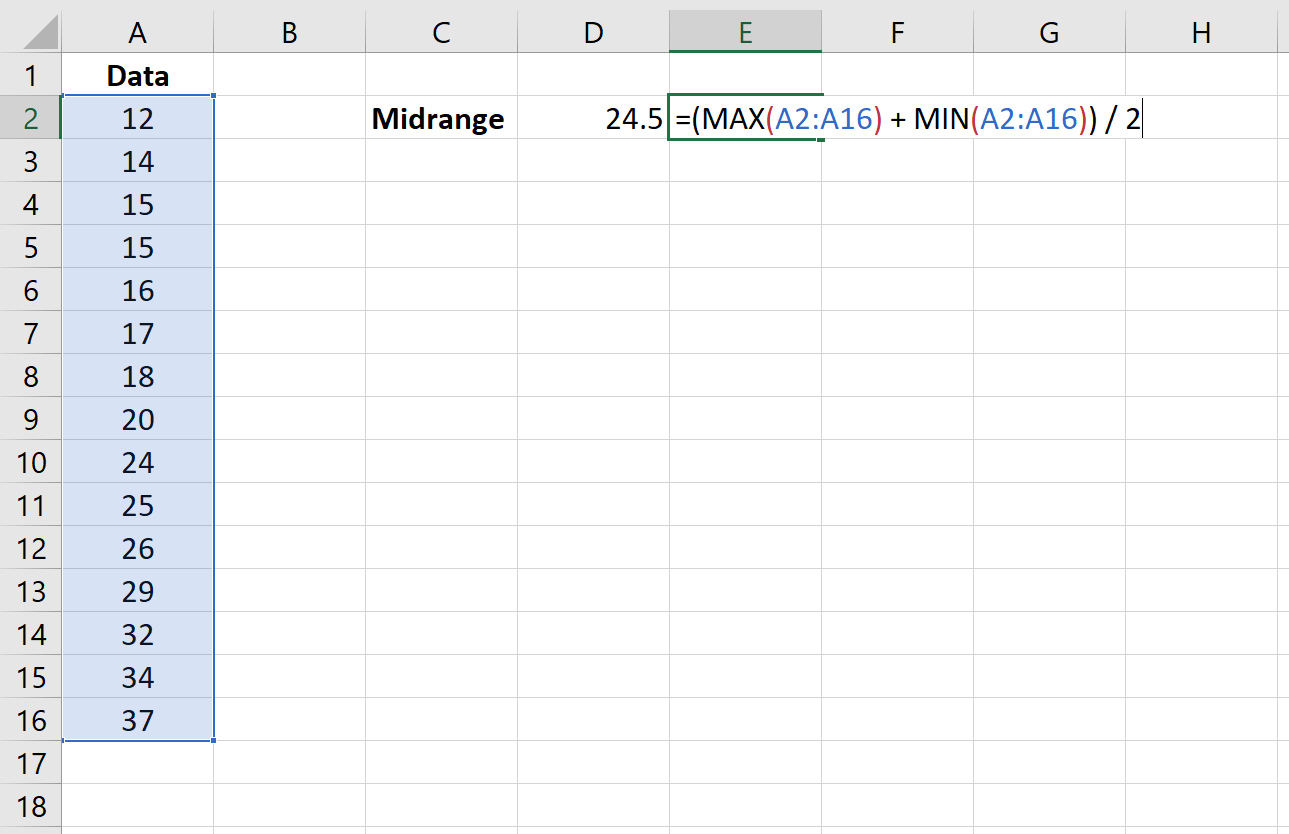
Средний диапазон для этого набора данных составляет 24,5 .
Недостаток использования среднего диапазона
Недостатком использования средних является тот факт, что на них могут легко влиять выбросы. Если минимальное значение набора данных необычно мало или максимальное значение необычно велико, это может оказать огромное влияние на расчет среднего значения.
Например, предположим, что максимальное значение в нашем наборе данных равно 120. Тогда средний диапазон будет равен 66:
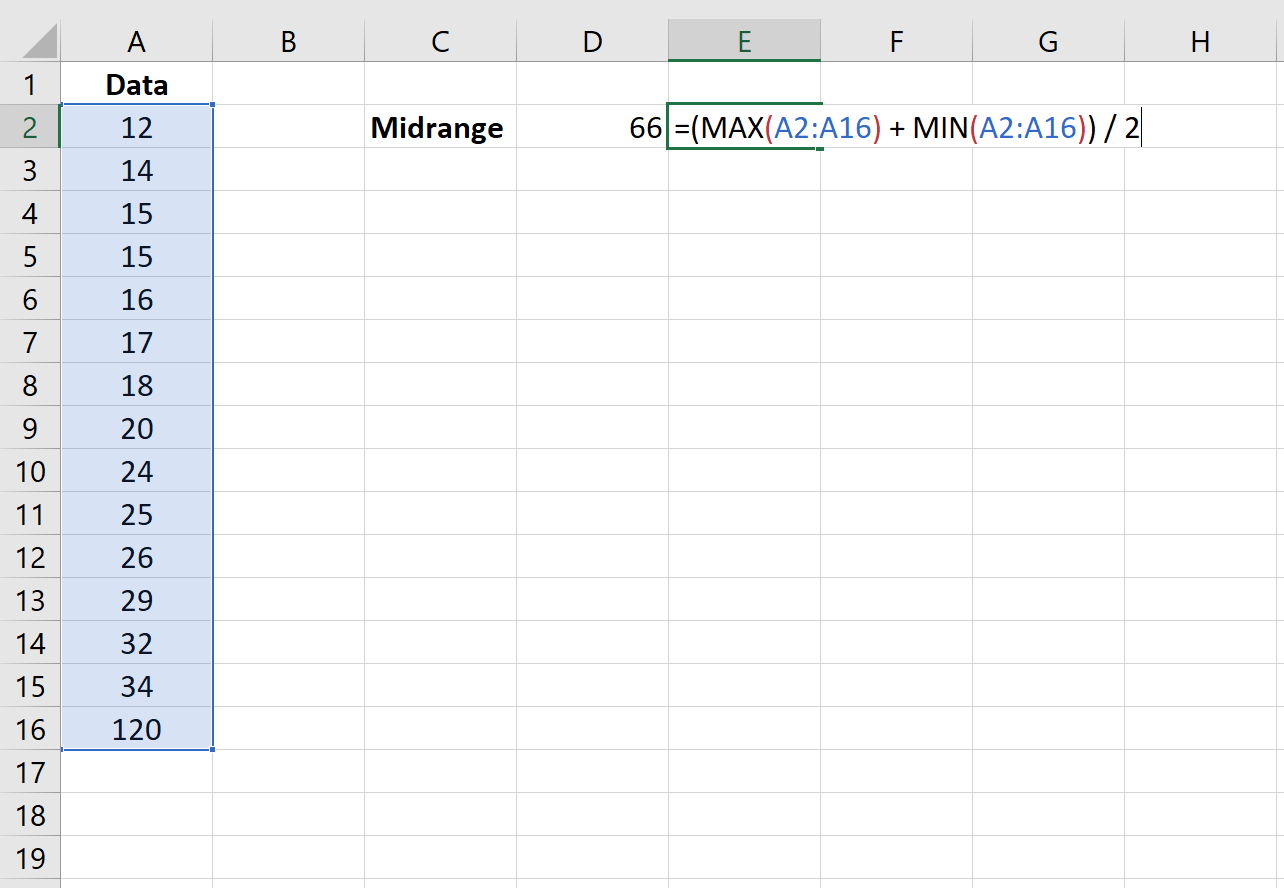
Напомним, что средний диапазон должен дать нам представление о том, где находится центр набора данных. Однако в этом сценарии, поскольку максимальное значение является выбросом, средний диапазон равен 66, что совсем не близко к центру нашего набора данных.
Альтернативы среднего уровня
На практике средний диапазон редко используется как способ вычисления центра набора данных просто потому, что существуют более качественные измерения, более устойчивые к выбросам. В частности, следующие два измерения, как правило, являются более точными измерениями центра :
Среднее: Среднее значение в наборе данных.
Медиана: медианное значение в наборе данных.
На следующем изображении показаны формулы, которые мы можем использовать для расчета среднего и медианы набора данных:
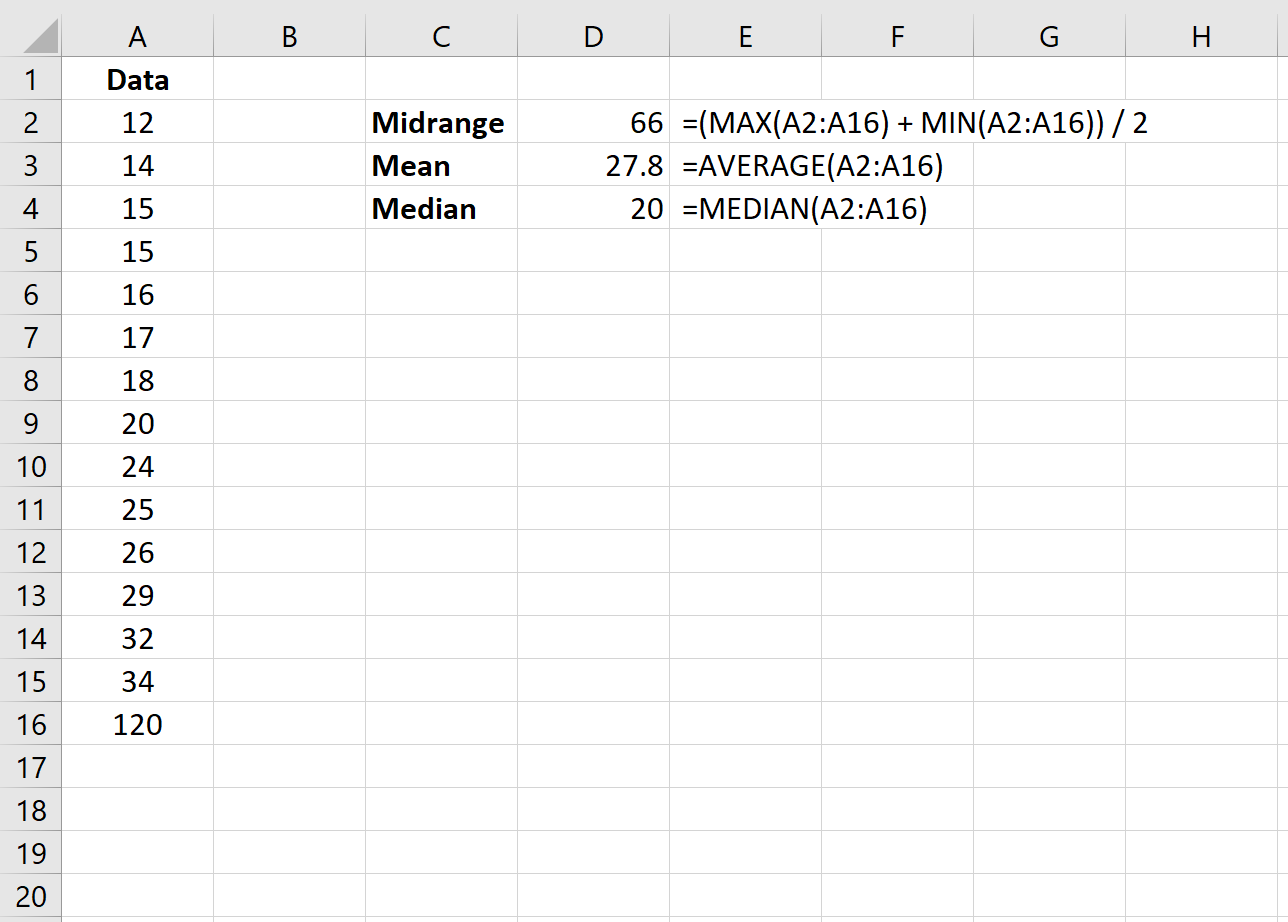
Обратите внимание, что выбросы лишь незначительно влияют на среднее значение, а на медиану это не влияет вообще.