Относительное стандартное отклонение
В этой статье объясняется, как рассчитать относительное стандартное отклонение. Вы узнаете, что такое относительное стандартное отклонение, какова его формула, а также пошагово решаемое упражнение.
Что такое относительное стандартное отклонение?
Относительное стандартное отклонение — это статистическая мера, которая указывает на дисперсию набора данных относительно его среднего значения. Относительное стандартное отклонение рассчитывается путем деления стандартного отклонения данных на их среднее значение.
Относительное стандартное отклонение выражается в процентах, и его значение всегда будет положительным.
Интерпретация относительного стандартного отклонения используется, чтобы показать дисперсию выборки данных. Чем больше значение относительного стандартного отклонения, тем более разбросаны данные. И чем меньше относительное стандартное отклонение, тем ближе данные к среднему значению.
Обычно аббревиатура RSD используется как символ относительного стандартного отклонения.
Формула относительного стандартного отклонения
Относительное стандартное отклонение равно стандартному отклонению, деленному на среднее значение, умноженному на 100. Следовательно, для расчета относительного стандартного отклонения необходимо сначала определить стандартное отклонение и среднее арифметическое, затем разделить два статистических измерения и, наконец, умножить на 100.
Другими словами, формула относительного стандартного отклонения выглядит следующим образом:
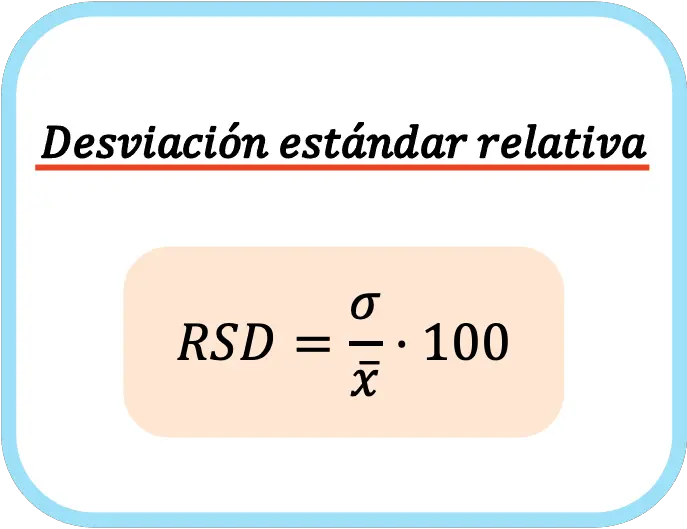
При расчете относительного стандартного отклонения его умножают на сто, чтобы выразить значение в процентах.
Пример расчета относительного стандартного отклонения
Изучив определение относительного стандартного отклонения и его формулу, ниже вы можете увидеть конкретный пример того, как рассчитывается относительное стандартное отклонение.
- Рассчитайте относительное стандартное отклонение следующего набора статистических данных:
4, 1, 3, 9, 12, 2, 5, 8, 3, 6
Сначала нам нужно найти стандартное отклонение данных:
Во-вторых, вычисляем среднее арифметическое данных:
Как только мы узнаем стандартное отклонение и среднее арифметическое ряда данных, мы используем формулу относительного стандартного отклонения.
И, наконец, подставляем рассчитанные значения в формулу и вычисляем относительное стандартное отклонение:
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше