Отрицательный бином против пуассона: как выбрать модель регрессии

Отрицательная биномиальная регрессия и регрессия Пуассона — это два типа моделей регрессии, которые следует использовать, когда переменная ответа представлена результатами дискретного подсчета.

Вот несколько примеров переменных ответа, которые представляют результаты дискретного подсчета:

• Количество студентов, окончивших определенную программу
• Количество дорожно-транспортных происшествий на определенном перекрестке
• Количество участников, прошедших марафон
• Количество возвратов в данном месяце в розничном магазине

Если дисперсия примерно равна среднему значению, то модель регрессии Пуассона обычно хорошо соответствует набору данных.

Однако если дисперсия значительно превышает среднее значение, модель отрицательной биномиальной регрессии обычно лучше соответствует данным.

Есть два метода, которые мы можем использовать, чтобы определить, является ли регрессия Пуассона или отрицательная биномиальная регрессия более подходящей для данного набора данных:

1. Остаточные участки

Мы можем создать график стандартизированных остатков в сравнении с прогнозируемыми значениями регрессионной модели.

Если большинство стандартизированных остатков находятся в диапазоне от -2 до 2, вероятно, подойдет модель регрессии Пуассона.

Однако если многие остатки выходят за пределы этого диапазона, модель отрицательной биномиальной регрессии, вероятно, обеспечит лучшее соответствие.

2. Тест отношения правдоподобия

Мы можем подогнать модель регрессии Пуассона и модель отрицательной биномиальной регрессии к одному и тому же набору данных, а затем выполнить тест отношения правдоподобия.

Если значение p теста ниже определенного уровня значимости (например, 0,05), то мы можем заключить, что модель отрицательной биномиальной регрессии обеспечивает значительно лучшее соответствие.

В следующем примере показано, как использовать эти два метода в R, чтобы определить, лучше ли использовать модель регрессии Пуассона или модель отрицательной биномиальной регрессии для данного набора данных.

Пример: отрицательная биномиальная регрессия против регрессии Пуассона

Предположим, мы хотим узнать, сколько стипендий получает бейсболист средней школы в данном округе в зависимости от его школьного подразделения («A», «B» или «C») и его школьной оценки. вступительный экзамен в университет (измеряется от 0 до 100). ).

Используйте следующие шаги, чтобы определить, обеспечивает ли модель отрицательной биномиальной регрессии или модель регрессии Пуассона лучшее соответствие данным.

Шаг 1. Создайте данные

Следующий код создает набор данных, с которым мы будем работать, который включает данные о 1000 бейсболистах:

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

Шаг 2. Подберите модель регрессии Пуассона и модель отрицательной биномиальной регрессии.

Следующий код показывает, как подогнать к данным модель регрессии Пуассона и модель отрицательной биномиальной регрессии:

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

Шаг 3. Создайте остаточные графики

Следующий код показывает, как построить графики остатков для обеих моделей.

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

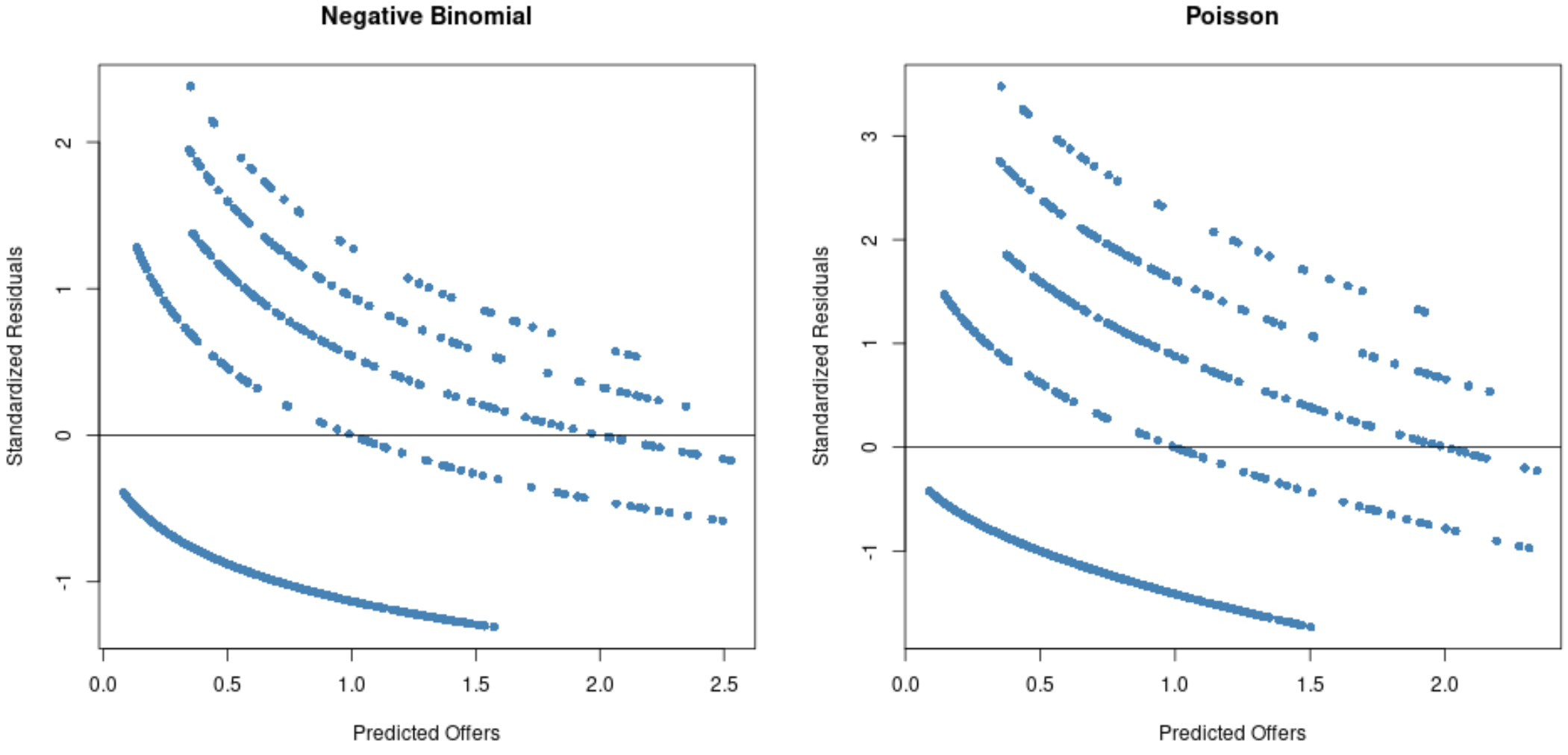
Из графиков мы видим, что остатки для модели регрессии Пуассона распределены больше (обратите внимание, что некоторые остатки выходят за пределы 3) по сравнению с моделью отрицательной биномиальной регрессии.

Это признак того, что модель отрицательной биномиальной регрессии, вероятно, более подходит, поскольку остатки этой модели меньше.

Шаг 4. Проведите тест отношения правдоподобия.

Наконец, мы можем выполнить тест отношения правдоподобия, чтобы определить, существует ли статистически значимая разница в подгонке двух регрессионных моделей:

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

Значение p теста оказалось равным 3,508072e-29 , что значительно меньше 0,05.

Таким образом, мы пришли к выводу, что модель отрицательной биномиальной регрессии обеспечивает значительно лучшее соответствие данным по сравнению с моделью регрессии Пуассона.

Дополнительные ресурсы

Введение в отрицательное биномиальное распределение
Введение в распределение Пуассона