Как выполнить повторные измерения anova в spss
ANOVA с повторными измерениями используется для определения того, существует ли статистически значимая разница между средними значениями трех или более групп, в которых одни и те же субъекты появляются в каждой группе.
В этом руководстве объясняется, как выполнить однофакторный дисперсионный анализ с повторными измерениями в SPSS.
Пример: дисперсионный анализ повторяющихся измерений в SPSS
Исследователи хотят знать, вызывают ли четыре разных препарата разное время реакции. Чтобы проверить это, они измерили время реакции пяти пациентов на четыре разных препарата. Поскольку у каждого пациента измеряется прием каждого из четырех лекарств, мы будем использовать дисперсионный анализ с повторными измерениями, чтобы определить, различается ли среднее время реакции между лекарствами.
Выполните следующие шаги, чтобы выполнить повторные измерения ANOVA в SPSS.
Шаг 1: Введите данные.
Введите следующие данные, которые показывают время реакции (в секундах) пяти пациентов на четыре лекарства:
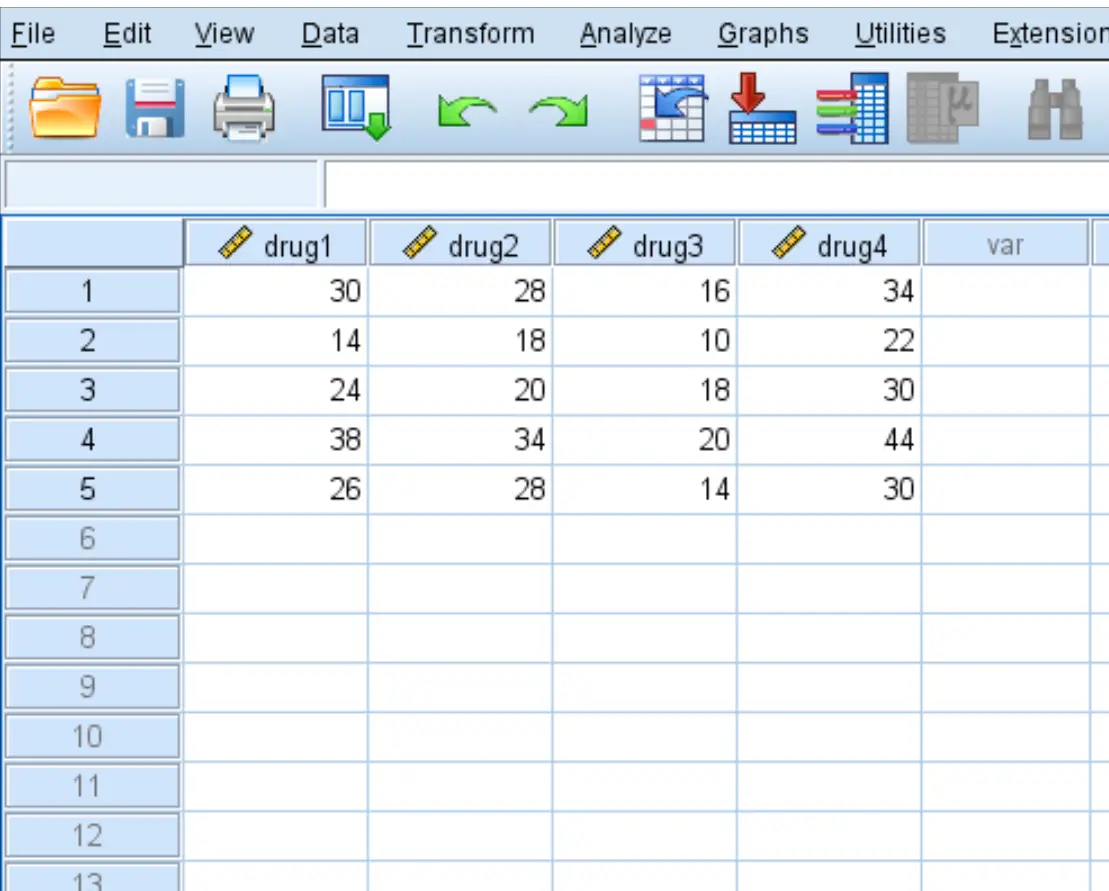
Шаг 2: Выполните повторные измерения ANOVA.
Перейдите на вкладку «Анализ» , затем «Общая линейная модель» , затем «Повторные измерения» :
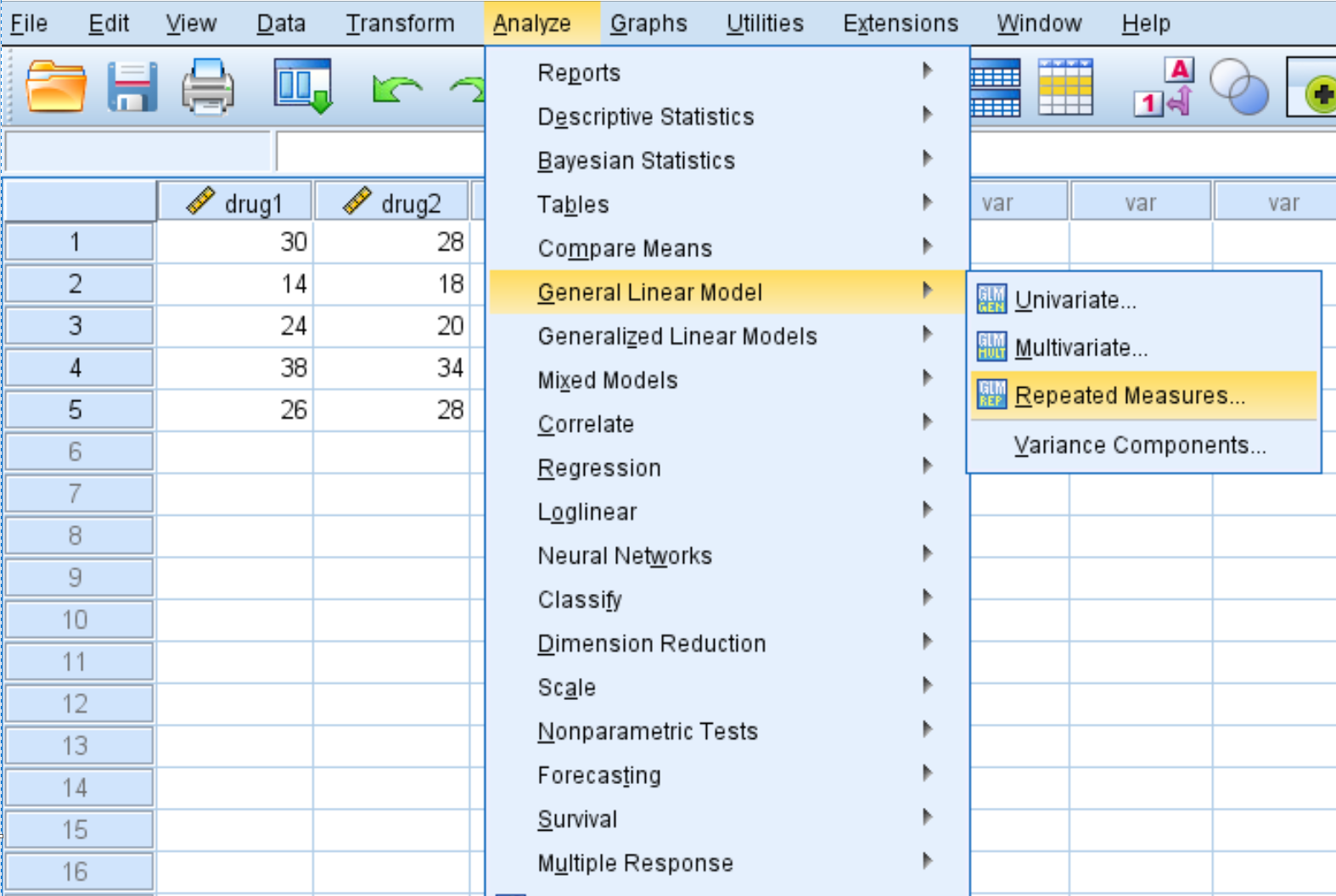
В появившемся новом окне введите препарат по названию внутрисубъектного фактора. Введите 4 в качестве количества уровней (поскольку каждый участник исследования тестировал 4 разных препарата), затем нажмите «Добавить» . Введите ResponseTime в поле «Имя меры» и нажмите «Добавить» . Наконец, нажмите «Установить» .
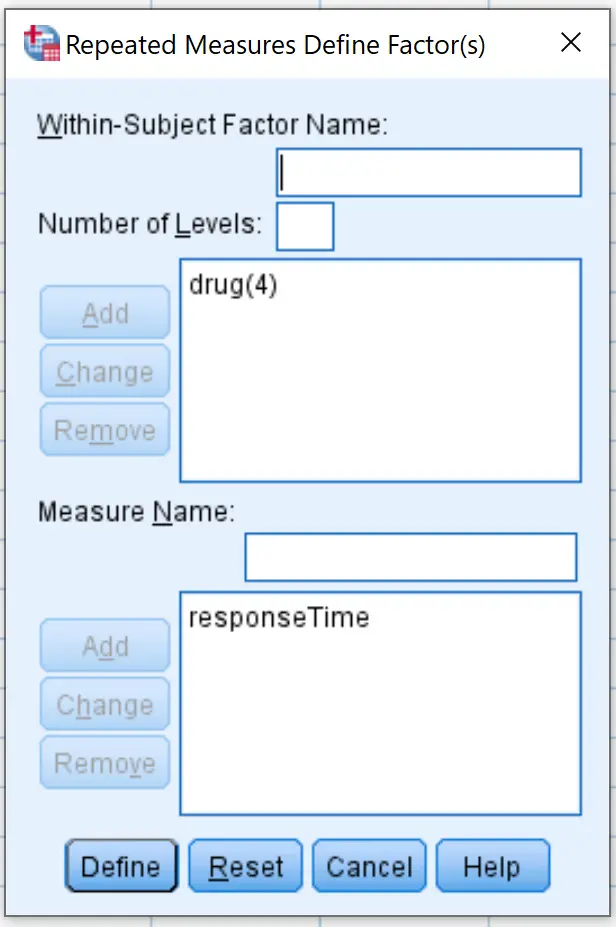
В появившемся новом окне перетащите каждую из четырех переменных препарата в область с надписью «Внутрисубъектные переменные» :
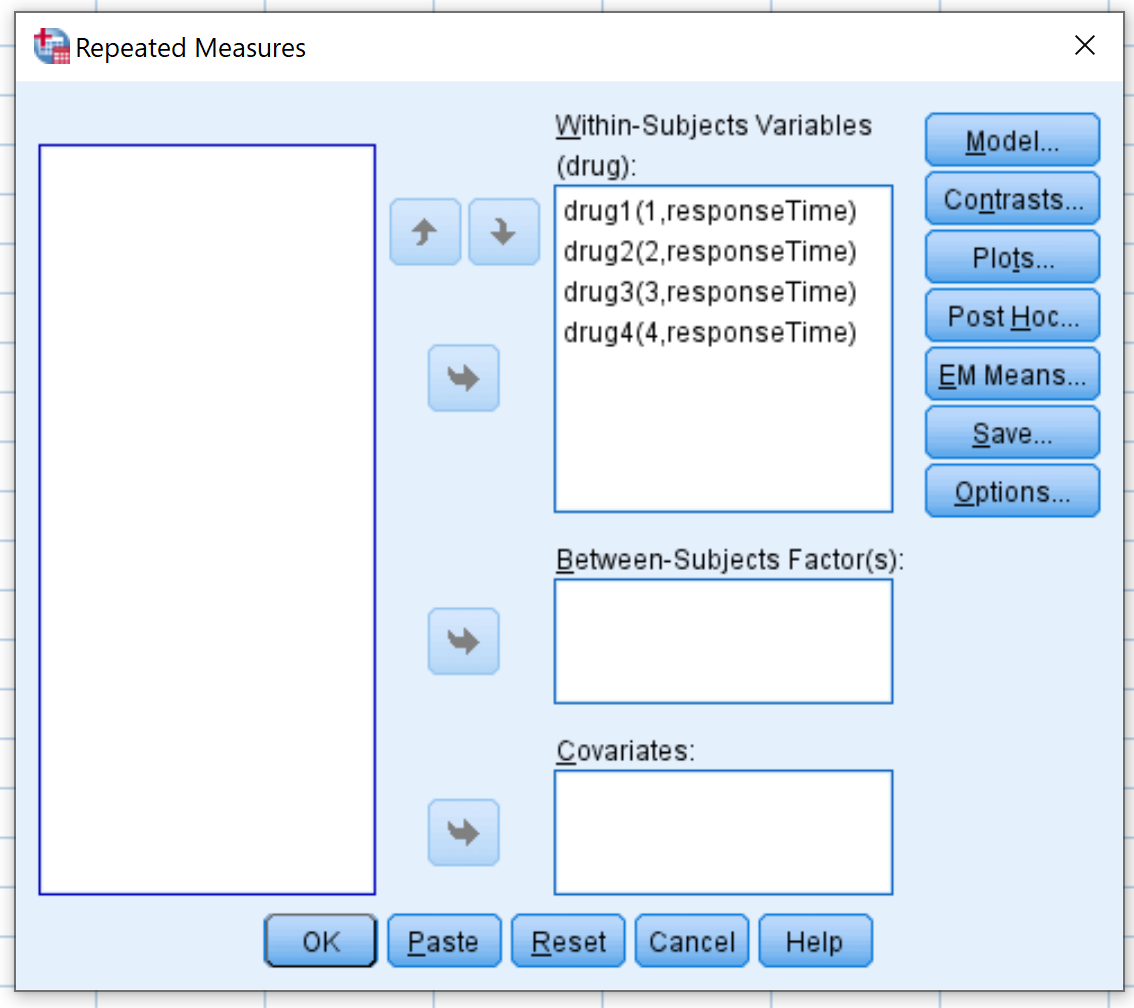
Далее нажмите Графики . Перетащите переменный препарат в область с надписью «Горизонтальная ось» . Затем нажмите Добавить . Затем нажмите Продолжить .
Далее нажмите EM Means . Перетащите переменную препарата в поле «Показать средства для» . Затем установите флажок «Сравнить основные эффекты» и выберите «Бонферрони» в раскрывающемся меню. Затем нажмите Продолжить .
Наконец, нажмите ОК .
Шаг 2: Интерпретируйте результаты.
Как только вы нажмете «ОК» , появятся результаты повторных измерений ANOVA. Вот как интерпретировать результат:
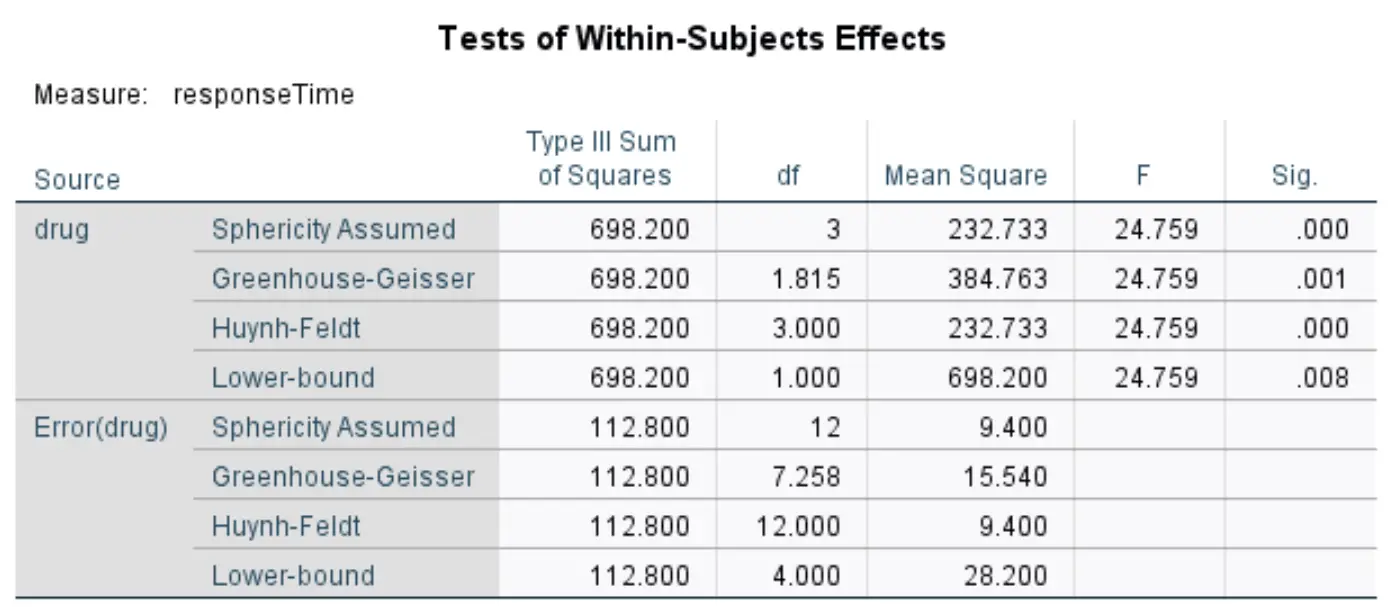
Тесты внутрисубъектных эффектов
В этой таблице отображена общая статистика F и соответствующее значение p из ANOVA с повторными измерениями. Обычно мы используем значения из строки с надписью Greenhouse-Geisser .
Согласно этой линии, статистика F равна 24,759 , а соответствующее значение p равно 0,001 . Поскольку это значение p меньше 0,05, мы можем отвергнуть нулевую гипотезу и заключить, что существует статистически значимая разница в среднем времени ответа между четырьмя препаратами.
Парные сравнения
Поскольку мы отвергли нулевую гипотезу, это означает, что по крайней мере два групповых средних различны. Чтобы определить, какие группы средств различаются, мы можем использовать эту таблицу, в которой показаны попарные сравнения каждого препарата.
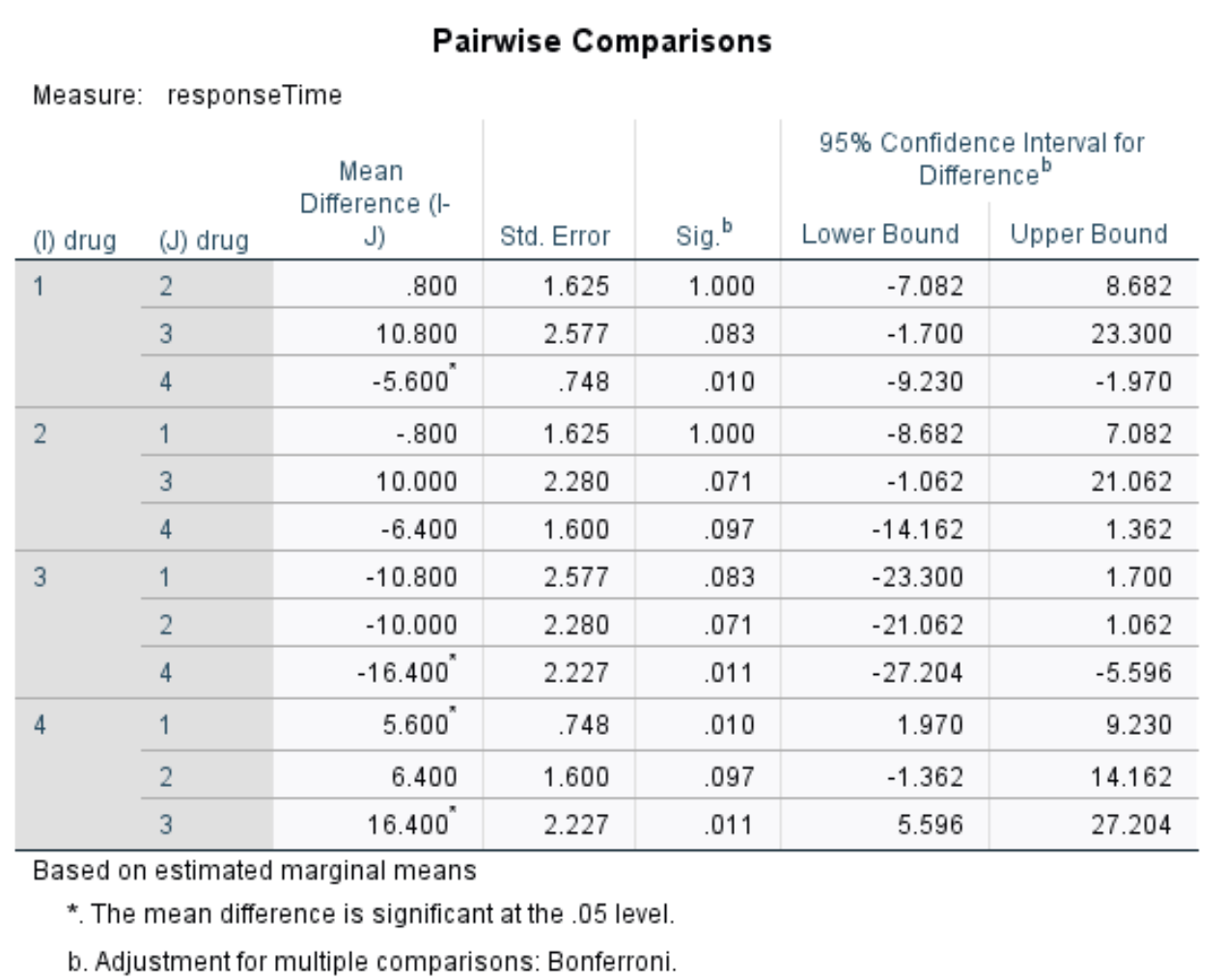
В таблице мы можем увидеть значения p для следующих сравнений:
- препарат 1 по сравнению с препаратом 2 | p-значение = 1,000
- препарат 1 по сравнению с препаратом 3 | р-значение = 0,083
- препарат 1 по сравнению с препаратом 4 | p-значение = 0,010
- препарат 2 по сравнению с препаратом 3 | р-значение = 0,071
- препарат 2 по сравнению с препаратом 4 | р-значение = 0,097
- препарат 3 по сравнению с препаратом 4 | р-значение = 0,011
Единственные значения p меньше 0,05 относятся к препарату 1 по сравнению с препаратом 4 и препарату 3 по сравнению с препаратом 4. Все остальные сравнения имеют значения p больше 0,05.
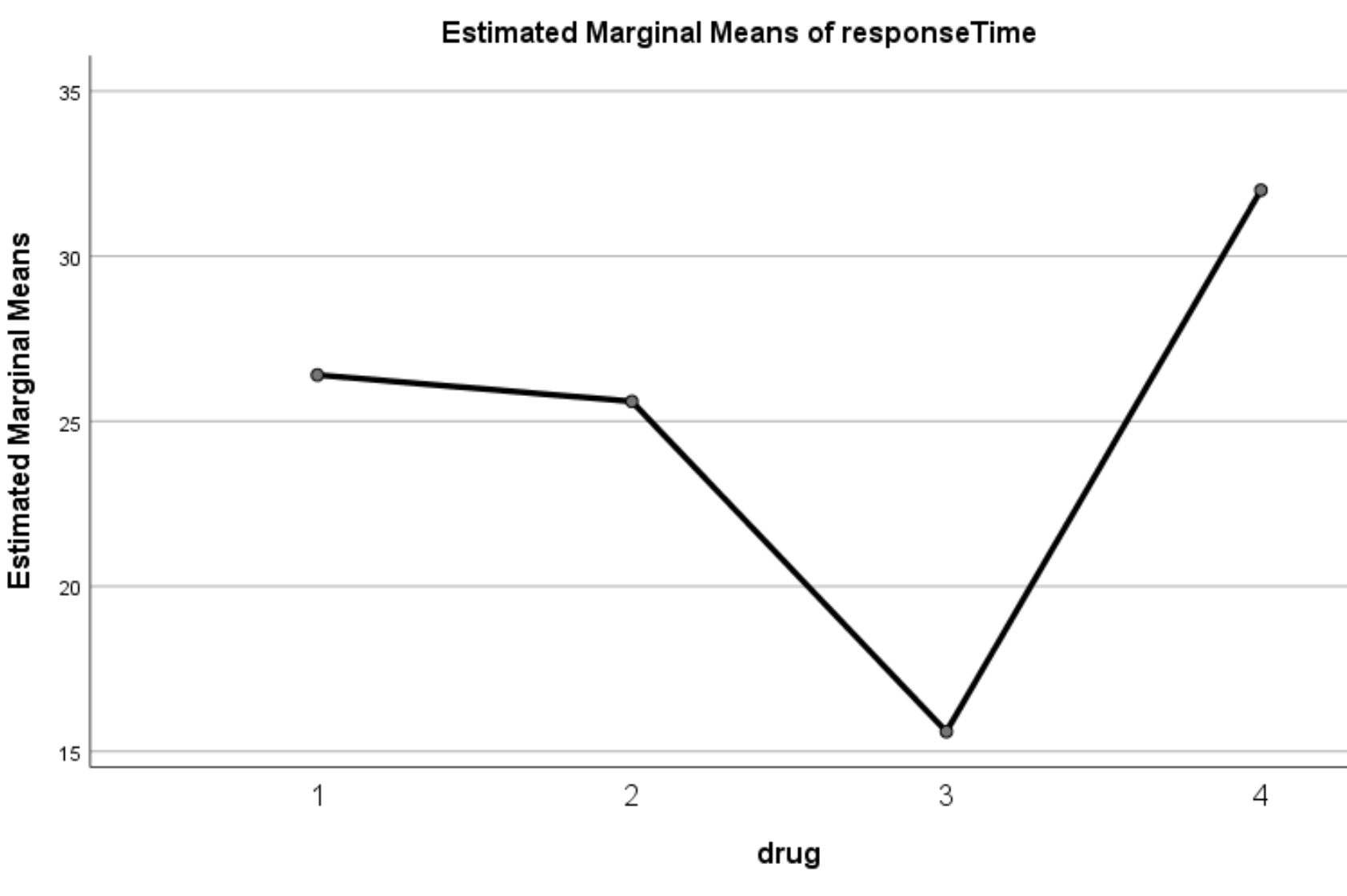
График предполагаемых предельных средних
На этой диаграмме показано примерное среднее время ответа для каждого лекарства. На графике мы ясно видим, что время ответа значительно различалось между четырьмя разными препаратами:
Шаг 3: Сообщите о результатах.
Наконец, мы можем сообщить о результатах повторных измерений ANOVA. Вот пример того, как это сделать:
Был проведен односторонний дисперсионный анализ с повторными измерениями, чтобы определить, различается ли среднее время реакции пациентов на четыре разных лекарства.
Однофакторный дисперсионный анализ с повторными измерениями показал, что тип используемого лекарства приводил к статистически значимым различиям во времени ответа (F = 24,75887, p = 0,001).
Тест Бонферрони для множественных сравнений выявил статистически значимую разницу во времени ответа между пациентами, принимавшими препарат 1 и препарат 4, а также препарат 3 и препарат 4.