Полиномиальная регрессия

К бенджамин андерсон 2 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое полиномиальная регрессия в статистике и как она выполняется. Дополнительно вы сможете увидеть пример, в котором выполняется полиномиальная регрессия.

Что такое полиномиальная регрессия?

Полиномиальная регрессия , или полиномиальная регрессия , — это модель регрессии, в которой связь между независимой переменной X и зависимой переменной Y моделируется с использованием полинома.

Например, уравнение для модели квадратичной полиномиальной регрессии имеет вид y=β ₀ +β ₁ x+β ₂ x ² +ε.

Полиномиальная регрессия полезна для подбора наборов данных, графики которых представляют собой полиномиальные кривые. Итак, если точечный график выборки данных имеет форму параболы, лучше построить модель квадратичной регрессии, а не модель линейной регрессии. Таким образом, уравнение модели регрессии будет лучше соответствовать выборке данных.

Обратите внимание, что полиномиальная регрессия — это тип нелинейной регрессии, такой же, как экспоненциальная регрессия и логарифмическая регрессия.

Формула полиномиальной регрессии

Уравнение модели полиномиальной регрессии: y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε.

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

Золото:

$y$

является зависимой переменной.
$x$

является независимой переменной.
$\beta_0$

– константа уравнения полиномиальной регрессии.
$\beta_i$

коэффициент регрессии, связанный с переменной

$x^i$

.
$\bm{\varepsilon}$

Это ошибка или остаток, то есть разница между наблюдаемым значением и значением, оцененным моделью.

Итак, если у нас есть образец с общим количеством

$n$

наблюдений, мы можем предложить модель полиномиальной регрессии в матричной форме:

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

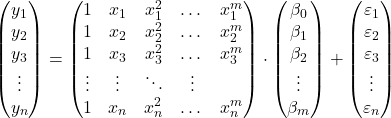
Приведенное выше матричное выражение можно переписать, присвоив каждой матрице букву:

$Y=X\beta+\varepsilon$

Таким образом, применив критерий наименьших квадратов , мы можем прийти к формуле оценки коэффициентов модели полиномиальной регрессии :

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

Однако выполнение этих расчетов вручную очень трудоемко и требует много времени, поэтому удобнее использовать компьютерное программное обеспечение (например, Minitab или Excel), которое позволяет гораздо быстрее выполнить модель полиномиальной регрессии.

Пример модели полиномиальной регрессии

Теперь, когда мы знаем определение полиномиальной регрессии и то, как она выполняется, давайте посмотрим на реальный пример, чтобы полностью понять эту концепцию.

Прежде всего, следует иметь в виду, что модель полиномиальной регрессии следует выполнять, когда график данных имеет форму полиномиальной кривой. Например, если точечный график имеет форму кубической кривой, нам необходимо построить модель полиномиальной регрессии третьей степени.

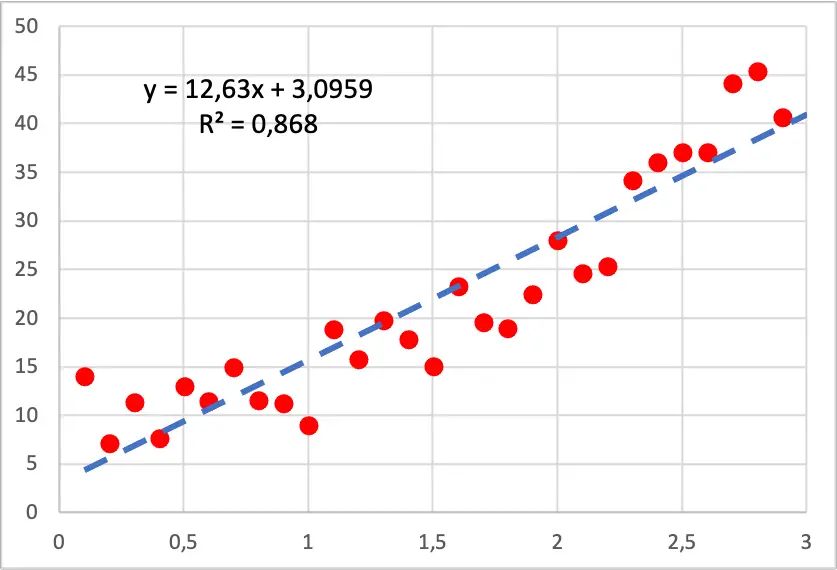
Итак, как вы видите на следующем изображении, точечный график наших данных имеет квадратичную форму, потому что, когда мы увеличиваем значение независимой переменной, зависимая переменная растет быстрее. В этом случае была создана модель линейной регрессии, и, как вы можете видеть, она плохо соответствует точкам, поскольку в ней есть участки, в которых линия находится ниже всех точек, и участки, в которых линия находится над ними.

С другой стороны, если мы запустим модель регрессии с квадратичным полиномом, она намного лучше соответствует выборочным данным, как вы можете видеть на изображении ниже.

Кроме того, при разработке модели полиномиальной регрессии коэффициент детерминации значительно улучшается, поскольку он увеличивается с 86,80% до 94,05%. Таким образом, новая регрессионная модель гораздо лучше объясняет набор данных.

С другой стороны, еще одним признаком того, что нам необходимо выполнить полиномиальную регрессию, является построение графика остатков. Если в линейной регрессии график остатков имеет форму параболы или полинома другого типа, модель полиномиальной регрессии наверняка лучше соответствует изучаемым данным.

Другие типы нелинейной регрессии

В основном существует три типа нелинейной регрессии:

Полиномиальная регрессия . Уравнение модели регрессии имеет форму полинома.
Логарифмическая регрессия : берется логарифм независимой переменной.
Экспоненциальная регрессия : независимая переменная находится в показателе степени уравнения.

➤ См.: Логарифмическая регрессия.
➤ См.: Экспоненциальная регрессия.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше