Как выполнить полиномиальную регрессию в python
Регрессионный анализ используется для количественной оценки взаимосвязи между одной или несколькими объясняющими переменными и переменной отклика.
Наиболее распространенным типом регрессионного анализа является простая линейная регрессия , используемая, когда переменная-предиктор и переменная отклика имеют линейную связь.

Однако иногда связь между переменной-предиктором и переменной отклика является нелинейной.
Например, истинная зависимость может быть квадратичной:
Или это может быть куб:

В этих случаях имеет смысл использовать полиномиальную регрессию , которая может учитывать нелинейные связи между переменными.
В этом руководстве объясняется, как выполнить полиномиальную регрессию в Python.
Пример: полиномиальная регрессия в Python
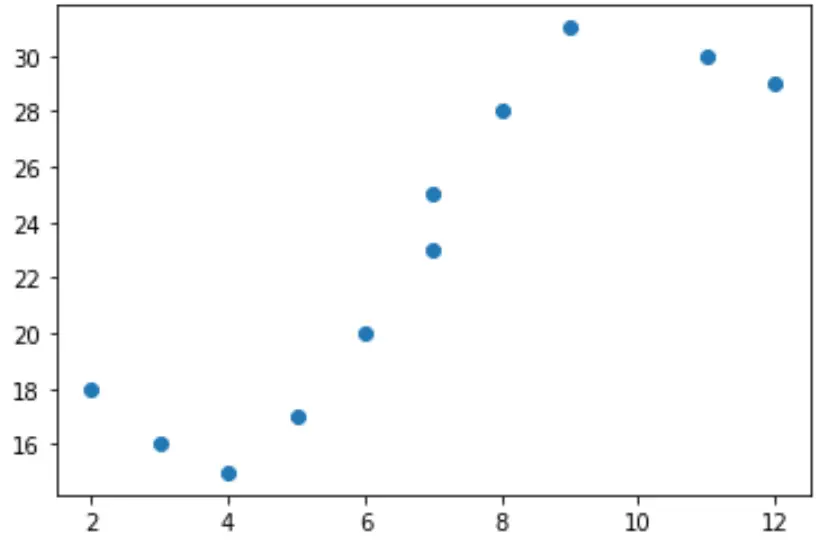
Предположим, у нас есть следующая переменная-предиктор (x) и переменная ответа (y) в Python:
x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12] y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]
Если мы создадим простую диаграмму рассеяния этих данных, мы увидим, что связь между x и y явно не линейна:
import matplotlib.pyplot as plt #create scatterplot plt.scatter(x, y)
Поэтому не имеет смысла подгонять к этим данным модель линейной регрессии. Вместо этого мы можем попытаться подогнать модель полиномиальной регрессии степени 3, используя функцию numpy.polyfit() :
import numpy as np #polynomial fit with degree = 3 model = np.poly1d(np.polyfit(x, y, 3)) #add fitted polynomial line to scatterplot polyline = np.linspace(1, 12, 50) plt.scatter(x, y) plt.plot(polyline, model(polyline)) plt.show()
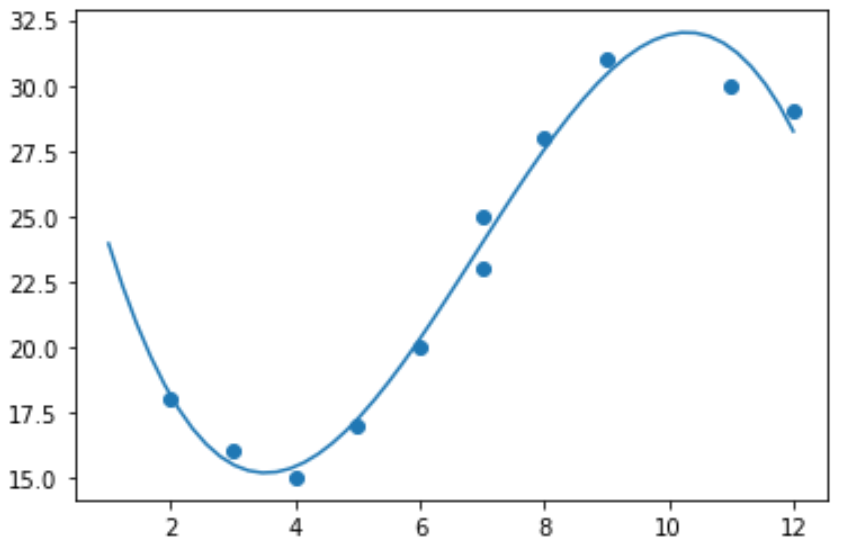
Мы можем получить уравнение полиномиальной регрессии, распечатав коэффициенты модели:
print(model) poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])
Подобранное уравнение полиномиальной регрессии:
у = -0,109х 3 + 2,256х 2 – 11,839х + 33,626
Это уравнение можно использовать для нахождения ожидаемого значения переменной отклика при заданном значении объясняющей переменной.
Например, предположим, что x = 4. Ожидаемое значение переменной ответа y будет следующим:
у = -0,109(4) 3 + 2,256(4) 2 – 11,839(4) + 33,626= 15,39 .
Мы также можем написать короткую функцию, чтобы получить R-квадрат модели, который представляет собой долю дисперсии переменной отклика, которую можно объяснить переменными-предикторами.
#define function to calculate r-squared def polyfit(x, y, degree): results = {} coeffs = numpy.polyfit(x, y, degree) p = numpy.poly1d(coeffs) #calculate r-squared yhat = p(x) ybar = numpy.sum(y)/len(y) ssreg = numpy.sum((yhat-ybar)**2) sstot = numpy.sum((y - ybar)**2) results['r_squared'] = ssreg / sstot return results #find r-squared of polynomial model with degree = 3 polyfit(x, y, 3) {'r_squared': 0.9841113454245183}
В этом примере квадрат R модели равен 0,9841 .
Это означает, что 98,41% вариаций переменной ответа можно объяснить переменными-предикторами.