Полиномиальная регрессия в r (шаг за шагом)
Полиномиальная регрессия — это метод, который мы можем использовать, когда связь между переменной-предиктором и переменной ответа является нелинейной.
Этот тип регрессии принимает форму:
Y = β 0 + β 1 X + β 2 X 2 + … + β h
где h — «степень» многочлена.
В этом руководстве представлен пошаговый пример выполнения полиномиальной регрессии в R.
Шаг 1. Создайте данные
В этом примере мы создадим набор данных, содержащий количество изученных часов и итоговую оценку за экзамен для класса из 50 учеников:
#make this example reproducible set.seed(1) #create dataset df <- data.frame(hours = runif (50, 5, 15), score=50) df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2) #view first six rows of data head(data) hours score 1 7.655087 64.30191 2 8.721239 70.65430 3 10.728534 73.66114 4 14.082078 86.14630 5 7.016819 59.81595 6 13.983897 83.60510
Шаг 2. Визуализируйте данные
Прежде чем подгонять регрессионную модель к данным, давайте сначала создадим диаграмму рассеяния, чтобы визуализировать взаимосвязь между учебными часами и баллами на экзамене:
library (ggplot2) ggplot(df, aes (x=hours, y=score)) + geom_point()
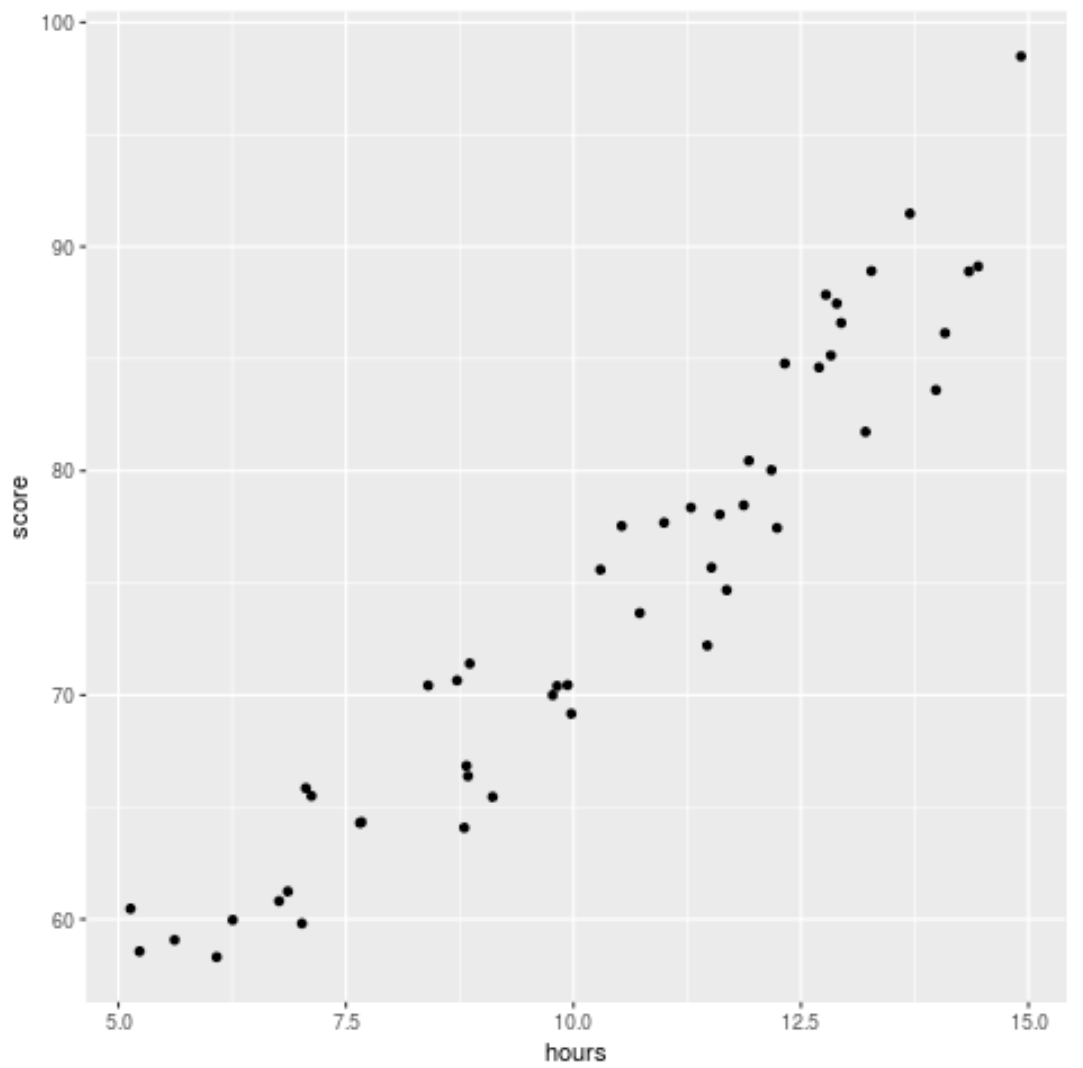
Мы видим, что данные имеют слегка квадратичную зависимость, что указывает на то, что полиномиальная регрессия может лучше соответствовать данным, чем простая линейная регрессия.
Шаг 3. Подбор моделей полиномиальной регрессии
Далее мы адаптируем пять различных моделей полиномиальной регрессии со степенями h = 1…5 и используем k-кратную перекрестную проверку с k = 10 раз, чтобы вычислить тест MSE для каждой модели:
#randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]
#define number of folds to use for k-fold cross-validation
K <- 10
#define degree of polynomials to fit
degree <- 5
#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )
#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)
#Perform K-fold cross validation
for (i in 1:K){
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
testData <- df.shuffled[testIndexes, ]
trainData <- df.shuffled[-testIndexes, ]
#use k-fold cv to evaluate models
for (j in 1:degree){
fit.train = lm (score ~ poly (hours,d), data=trainData)
fit.test = predict (fit.train, newdata=testData)
mse[i,j] = mean ((fit.test-testData$score)^2)
}
}
#find MSE for each degree
colMeans(mse)
[1] 9.802397 8.748666 9.601865 10.592569 13.545547
В результате мы видим тест MSE для каждой модели:
- Тест MSE со степенью h = 1: 9,80
- Тест MSE со степенью h = 2: 8,75
- Тест MSE со степенью h = 3: 9,60
- Тест MSE со степенью h = 4: 10,59
- Тест MSE со степенью h=5: 13,55
Модель с наименьшим тестовым MSE оказалась моделью полиномиальной регрессии со степенью h = 2.
Это соответствует нашему интуитивному выводу из исходной диаграммы рассеяния: модель квадратичной регрессии лучше всего соответствует данным.
Шаг 4. Анализ окончательной модели
Наконец, мы можем получить коэффициенты наиболее эффективной модели:
#fit best model best = lm (score ~ poly (hours,2, raw= T ), data=df) #view summary of best model summary(best) Call: lm(formula = score ~ poly(hours, 2, raw = T), data = df) Residuals: Min 1Q Median 3Q Max -5.6589 -2.0770 -0.4599 2.5923 4.5122 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 54.00526 5.52855 9.768 6.78e-13 *** poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569 poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Из результата мы видим, что окончательная подобранная модель:
Оценка = 54,00526 – 0,07904*(часы) + 0,18596*(часы) 2
Мы можем использовать это уравнение для оценки оценки, которую получит студент в зависимости от количества изученных часов.
Например, студент, который учится 10 часов, должен получить оценку 71,81 :
Оценка = 54,00526 – 0,07904*(10) + 0,18596*(10) 2 = 71,81
Мы также можем построить подобранную модель, чтобы увидеть, насколько хорошо она соответствует необработанным данным:
ggplot(df, aes (x=hours, y=score)) + geom_point() + stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + xlab(' Hours Studied ') + ylab(' Score ')
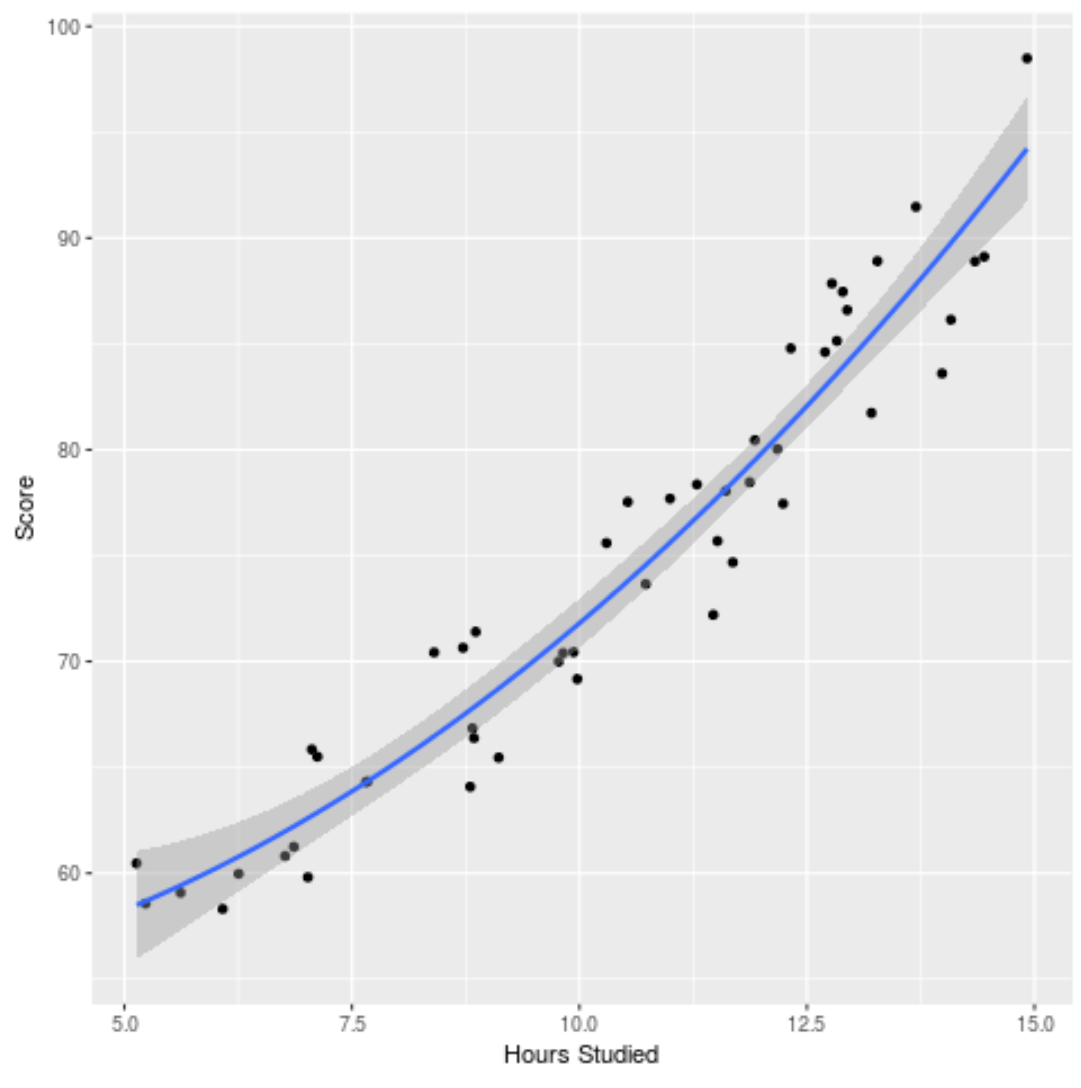
Полный код R, использованный в этом примере, вы можете найти здесь .