Как выполнить полиномиальную регрессию в sas
Наиболее распространенным типом регрессионного анализа является простая линейная регрессия , используемая, когда переменная-предиктор и переменная отклика имеют линейную связь.
Однако иногда связь между переменной-предиктором и переменной отклика является нелинейной.
В этих случаях имеет смысл использовать полиномиальную регрессию , которая может учитывать нелинейные связи между переменными.
В следующем примере показано, как выполнить полиномиальную регрессию в SAS.
Пример: полиномиальная регрессия в SAS
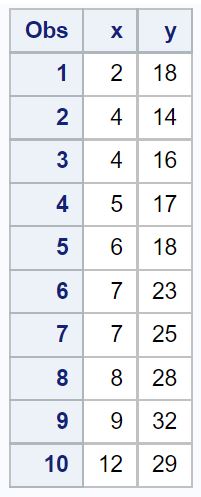
Предположим, у нас есть следующий набор данных в SAS:
/*create dataset*/ data my_data; input xy; datalines ; 2 18 4 14 4 16 5 17 6 18 7 23 7 25 8 28 9 32 12 29 ; run ; /*view dataset*/ proc print data =my_data;
Теперь предположим, что мы создаем диаграмму рассеяния для визуализации взаимосвязи между переменными x и y в наборе данных:
/*create scatter plot of x vs. y*/
proc sgplot data =my_data;
scatter x =x y =y;
run ;
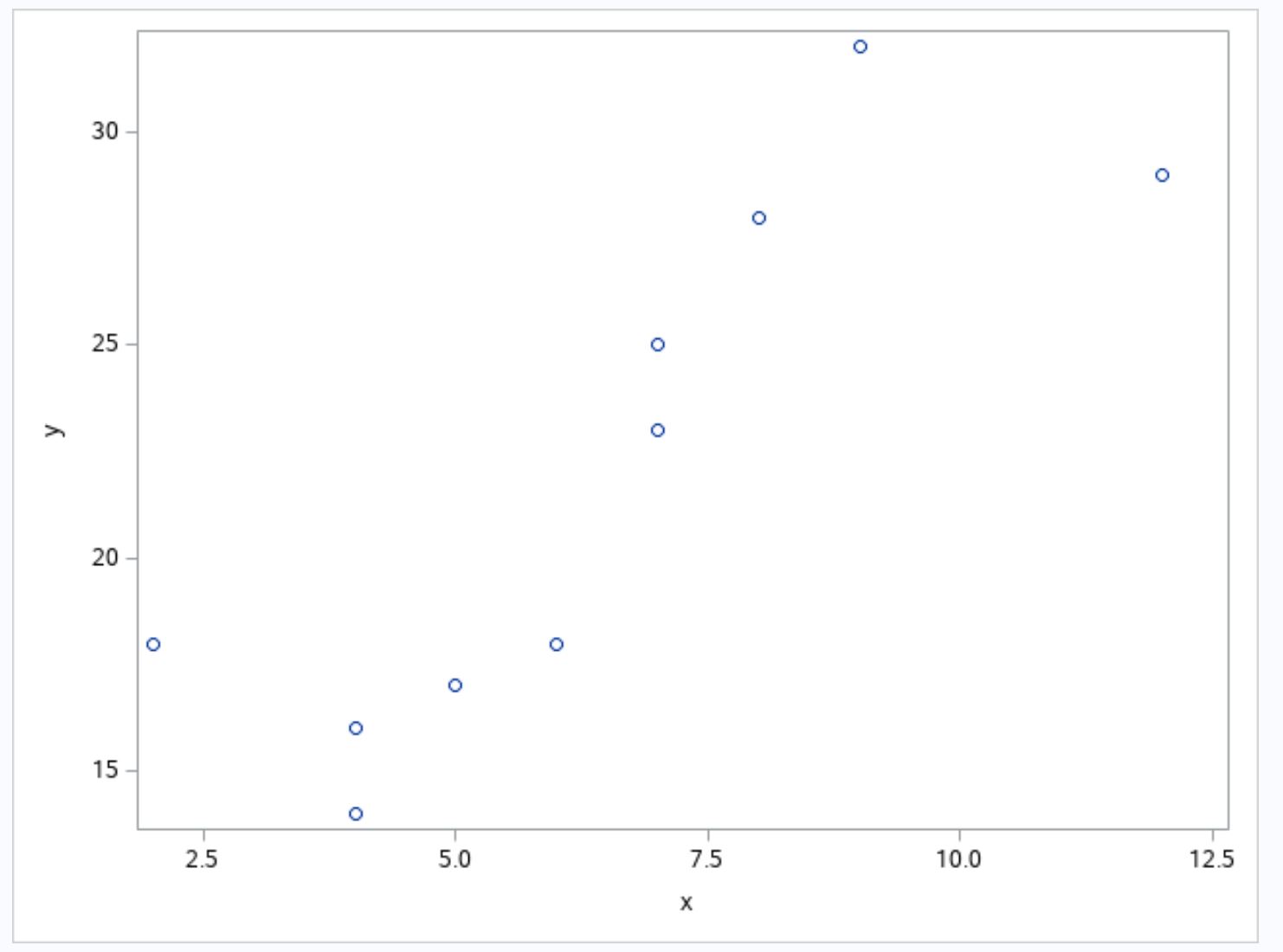
Из графика мы видим, что связь между x и y выглядит кубической.
Итак, мы можем определить две новые переменные-предикторы в нашем наборе данных (x 2 и x 3 ), а затем использовать proc reg для подбора модели полиномиальной регрессии с использованием этих переменных-предикторов:
/*create dataset with new predictor variables*/ data my_data; input xy; x2 = x** 2 ; x3 = x** 3 ; datalines ; 2 18 4 14 4 16 5 17 6 18 7 23 7 25 8 28 9 32 12 29 ; run ; /*fit polynomial regression model*/ proc reg data =my_data; model y = x x2 x3; run ;
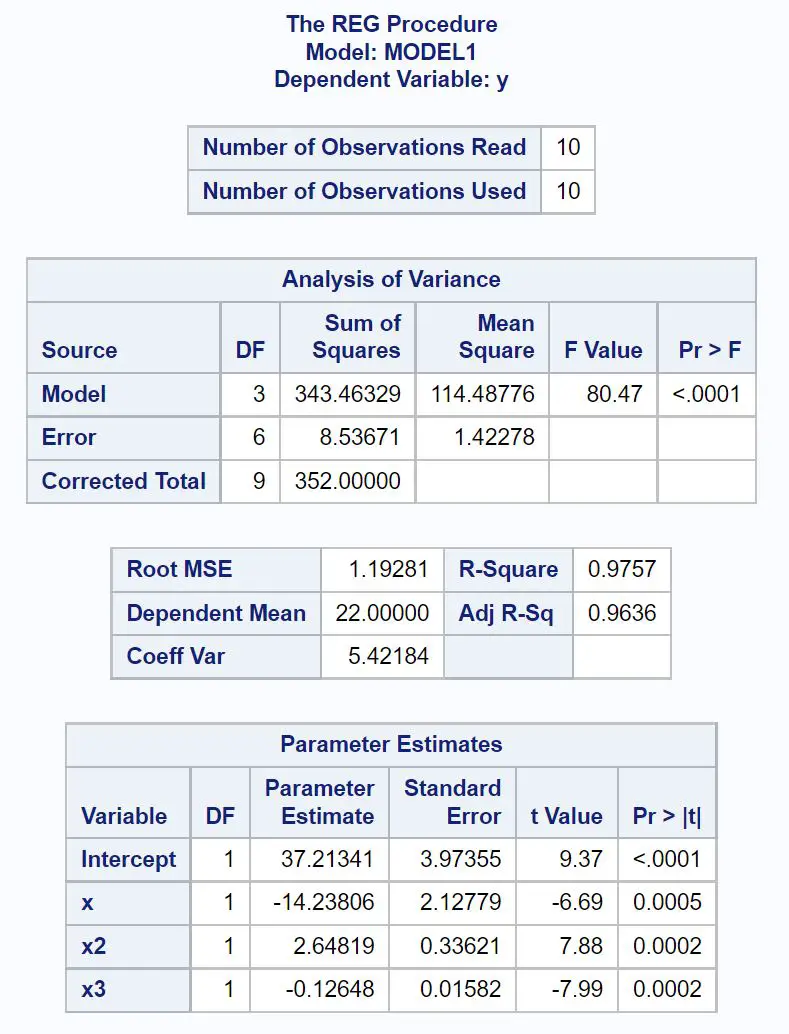
Из таблицы «Оценки параметров» мы можем найти оценки коэффициентов и записать уравнение подобранной полиномиальной регрессии следующим образом:
у = 37,213 – 14,238х + 2,648х 2 – 0,126х 3
Это уравнение можно использовать для нахождения ожидаемого значения переменной отклика при заданном значении предикторной переменной.
Например, если xa имеет значение 4, то y должно иметь значение 14,565:
у = 37,213 – 14,238(4) + 2,648(4) 2 – 0,126(4) 3 = 14,565
Мы также видим, что модель полиномиальной регрессии имеет скорректированное значение R-квадрата 0,9636 , которое очень близко к единице и говорит нам о том, что модель отлично справляется с подгонкой набора данных.
Связанный: Как интерпретировать скорректированный R-квадрат (с примерами)
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в SAS:
Как выполнить простую линейную регрессию в SAS
Как выполнить множественную линейную регрессию в SAS
Как выполнить квантильную регрессию в SAS