Как выполнить коррекцию бонферрони в r
Однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.
Если общее значение p таблицы ANOVA ниже определенного уровня значимости, то у нас есть достаточно доказательств, чтобы сказать, что по крайней мере одно из групповых средних значений отличается от других.
Однако это не говорит нам о том, какие группы отличаются друг от друга. Это просто говорит нам о том, что не все средние значения по группам одинаковы.
Чтобы точно знать, какие группы отличаются друг от друга, нам нужно выполнить попарные t-тесты между каждой группой, контролируя при этом частоту ошибок по семействам .
Один из наиболее распространенных способов добиться этого — использовать поправку Бонферрони при вычислении значений p для каждого из парных t-тестов.
В этом уроке объясняется, как выполнить коррекцию Бонферрони в R.
Пример: поправка Бонферрони в R
Предположим, учитель хочет знать, приводят ли три разных метода обучения к разным результатам тестов среди учащихся.
Чтобы проверить это, она случайным образом поручает 10 ученикам использовать каждый метод обучения. После недели использования назначенной им методики обучения каждый студент сдает один и тот же экзамен.
Мы можем использовать следующие шаги в R, чтобы подобрать однофакторный дисперсионный анализ, и использовать поправку Бонферрони для расчета попарных различий между результатами экзаменов каждой группы.
Шаг 1: Создайте набор данных.
Следующий код показывает, как создать набор данных, содержащий результаты экзаменов всех 30 студентов:
#create data frame data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ), score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89, 81, 82, 83, 83, 83, 84, 87, 90, 92, 93, 77, 78, 79, 88, 89, 90, 91, 95, 95, 98)) #view first six rows of data frame head(data) technical score 1 tech1 76 2 tech1 77 3 tech1 77 4 tech1 81 5 tech1 82 6 tech1 82
Шаг 2. Просмотрите результаты экзамена для каждой группы.
Следующий код показывает, как создать коробчатые диаграммы для визуализации распределения результатов экзамена для каждой группы:
boxplot(score ~ technique,
data = data,
main = "Exam Scores by Studying Technique",
xlab = "Studying Technique",
ylab = "Exam Scores",
col = "steelblue",
border = "black")
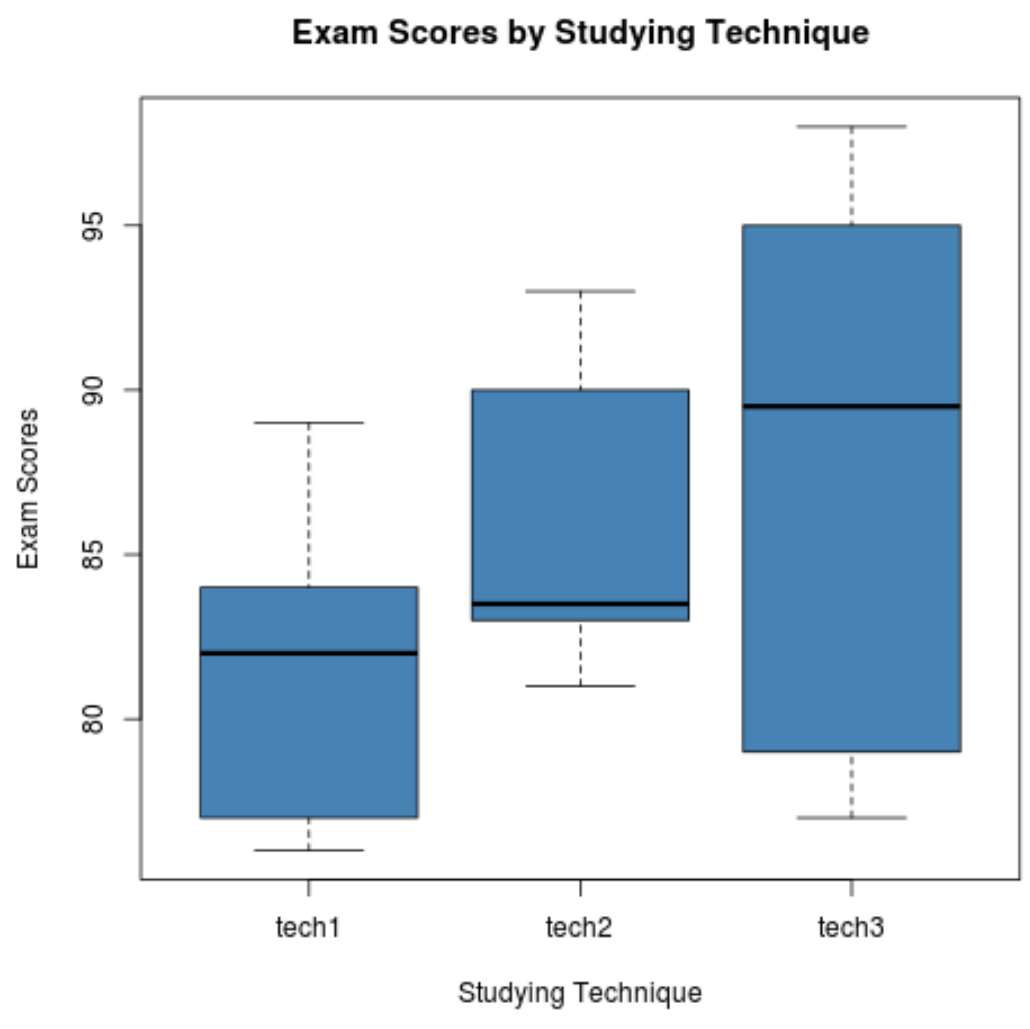
Шаг 3: Выполните односторонний дисперсионный анализ.
Следующий код показывает, как выполнить однофакторный дисперсионный анализ для проверки различий между средними баллами экзамена в каждой группе:
#fit the one-way ANOVA model model <- aov(score ~ technique, data = data) #view model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) technical 2 211.5 105.73 3.415 0.0476 * Residuals 27 836.0 30.96 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Поскольку общее значение p ( 0,0476 ) меньше 0,05, это указывает на то, что каждая группа не имеет одинаковый средний балл на экзамене.
Далее мы проведем попарные t-тесты, используя поправку Бонферрони для значений p, чтобы вычислить попарные различия между результатами экзаменов каждой группы.
Шаг 4: Выполните парные t-тесты.
Чтобы выполнить попарные t-тесты с поправкой Бонферрони в R, мы можем использовать функциюpairwise.t.test () , которая использует следующий синтаксис:
parwise.t.test(x, g, p.adjust.method=»bonferroni»)
Золото:
- x: числовой вектор значений ответа
- g: вектор, задающий названия групп (например, методика обучения).
Следующий код показывает, как использовать эту функцию для нашего примера:
#perform pairwise t-tests with Bonferroni's correction pairwise.t.test(data$score, data$technique, p.adjust.method=" bonferroni ") Pairwise comparisons using t tests with pooled SD data: data$score and data$technique tech1 tech2 tech2 0.309 - tech3 0.048 1.000 P value adjustment method: bonferroni
Интерпретация результата следующая:
- Скорректированное значение p для средней разницы в баллах на экзамене между Методикой 1 и Методикой 2 составляет 0,309 .
- Скорректированное значение p для средней разницы в баллах на экзамене между Методикой 1 и Техникой 3 составляет 0,048 .
- Скорректированное значение p для средней разницы в баллах на экзамене между Методикой 2 и Техникой 3 составляет 1000 .
Основываясь на результатах, мы видим, что единственная существенная разница есть между методом 1 и методом 3.
Дополнительные ресурсы
Введение в однофакторный дисперсионный анализ
Как выполнить односторонний дисперсионный анализ в R
Как выполнить тест Тьюки в R
Как выполнить тест Даннетта в R