Как построить биномиальное распределение в r
Чтобы построить функцию массы вероятности для биномиального распределения в R, мы можем использовать следующие функции:
- dbinom(x, size,prob) для создания функции вероятностной массы
- plot(x, y, type = ‘h’) для построения функции массы вероятности, указывая, что график представляет собой гистограмму (type=’h’)
Чтобы построить функцию массы вероятности, просто укажите размер (например, количество попыток) и вероятность (например, вероятность успеха в данном испытании) в функции dbinom() .
Например, следующий код показывает, как построить график функции массы вероятности для биномиального распределения с размером = 20 и вероятностью = 0,3:
success <- 0:20 plot(success, dbinom(success, size=20, prob=.3), type='h')
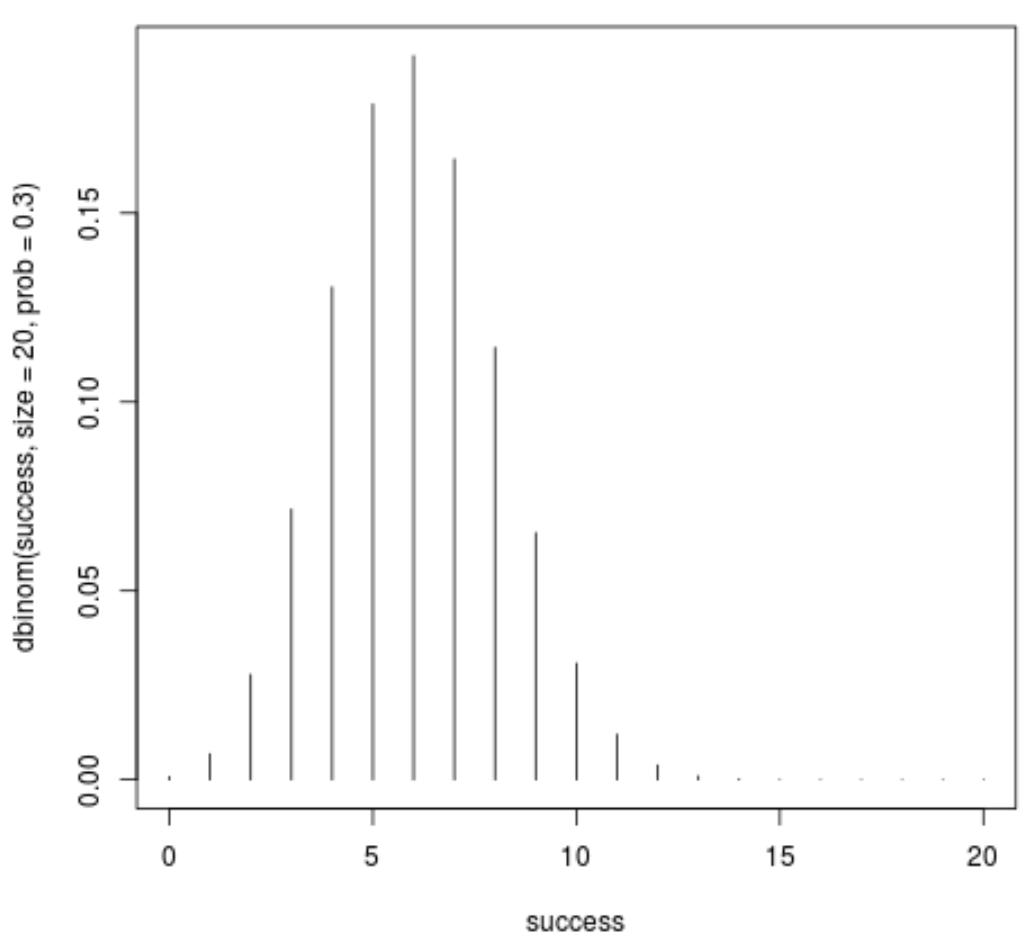
Ось X показывает количество успехов, а ось Y показывает вероятность получения такого количества успехов в 20 испытаниях.
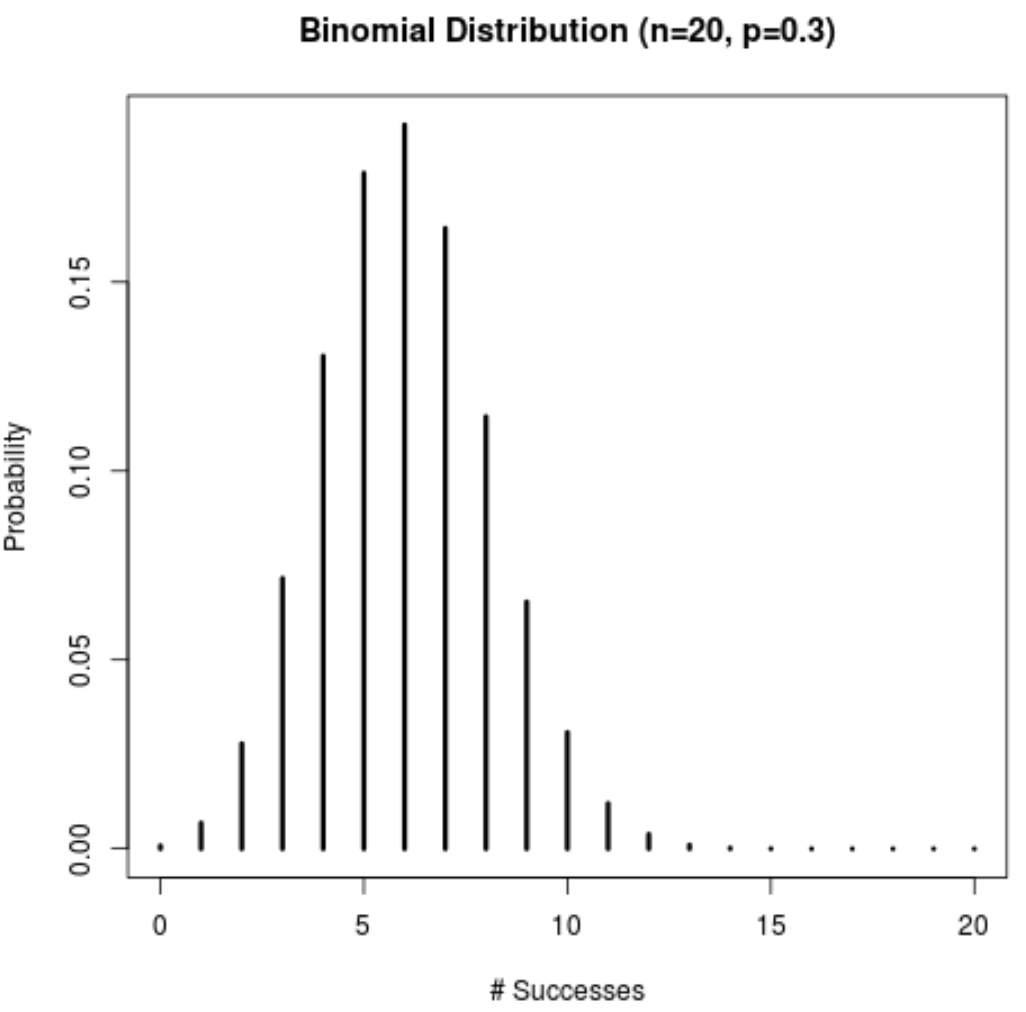
Мы можем добавить заголовок, изменить метки осей и увеличить ширину линий, чтобы сделать график более эстетичным:
success <- 0:20
plot(success,dbinom(success,size=20,prob=.3),
type='h',
main='Binomial Distribution (n=20, p=0.3)',
ylab='Probability',
xlab ='# Successes',
lwd=3)
Вы можете использовать следующий код, чтобы получить фактические вероятности для каждого количества успехов, отображаемых на диаграмме:
#prevent R from displaying numbers in scientific notation options(scipen=999) #define range of successes success <- 0:20 #display probability of success for each number of trials dbinom(success, size=20, prob=.3) [1] 0.00079792266297612 0.00683933711122388 0.02784587252426865 [4] 0.07160367220526231 0.13042097437387065 0.17886305056987975 [7] 0.19163898275344257 0.16426198521723651 0.11439673970486122 [10] 0.06536956554563482 0.03081708090008504 0.01200665489613703 [13] 0.00385928193090119 0.00101783259716075 0.00021810698510587 [16] 0.00003738976887529 0.00000500755833151 0.00000050496386536 [19] 0.00000003606884753 0.00000000162716605 0.00000000003486784
Дополнительные ресурсы
Введение в биномиальное распределение
Понимание формы биномиального распределения