Как построить кривую полиномиальной регрессии в r
Полиномиальная регрессия — это метод регрессии, который мы используем, когда связь между переменной-предиктором и переменной ответа является нелинейной.
В этом руководстве объясняется, как построить кривую полиномиальной регрессии в R.
Связанный: 7 наиболее распространенных типов регрессии
Пример: построение кривой полиномиальной регрессии в R
Следующий код показывает, как подогнать модель полиномиальной регрессии к набору данных, а затем построить кривую полиномиальной регрессии на необработанных данных на диаграмме рассеяния:
#define data x <- runif(50, 5, 15) y <- 0.1*x^3 - 0.5 * x^2 - x + 5 + rnorm(length(x),0,10) #plot x vs. y plot(x, y, pch= 16 , cex= 1.5 ) #fit polynomial regression model fit <- lm(y ~ x + I(x^2) + I(x^3)) #use model to get predicted values pred <- predict(fit) ix <- sort(x, index. return = T )$ix #add polynomial curve to plot lines(x[ix], pred[ix], col=' red ', lwd= 2 )
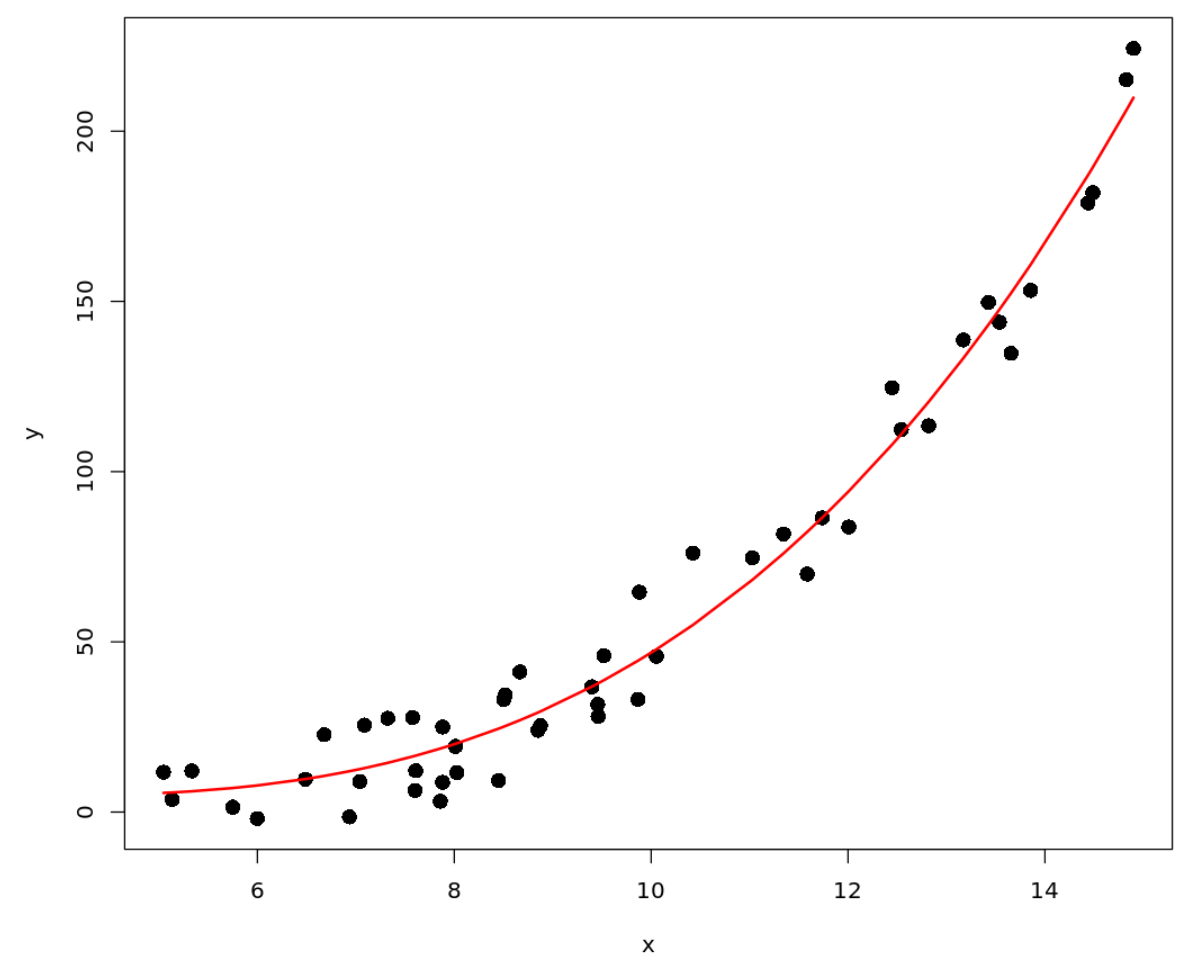
Мы также можем добавить уравнение полиномиальной регрессии на график, используя функцию text() :
#define data x <- runif(50, 5, 15) y <- 0.1*x^3 - 0.5 * x^2 - x + 5 + rnorm(length(x),0,10) #plot x vs. y plot(x, y, pch=16, cex=1.5) #fit polynomial regression model fit <- lm(y ~ x + I(x^2) + I(x^3)) #use model to get predicted values pred <- predict(fit) ix <- sort(x, index. return = T )$ix #add polynomial curve to plot lines(x[ix], pred[ix], col=' red ', lwd= 2 ) #get model coefficients coeff <- round(fit$coefficients, 2) #add fitted model equation to plot text(9, 200 , paste("Model: ", coeff[1], " + ", coeff[2], "*x", "+", coeff[3], "*x^2", "+", coeff[4], "*x^3"), cex= 1.3 )
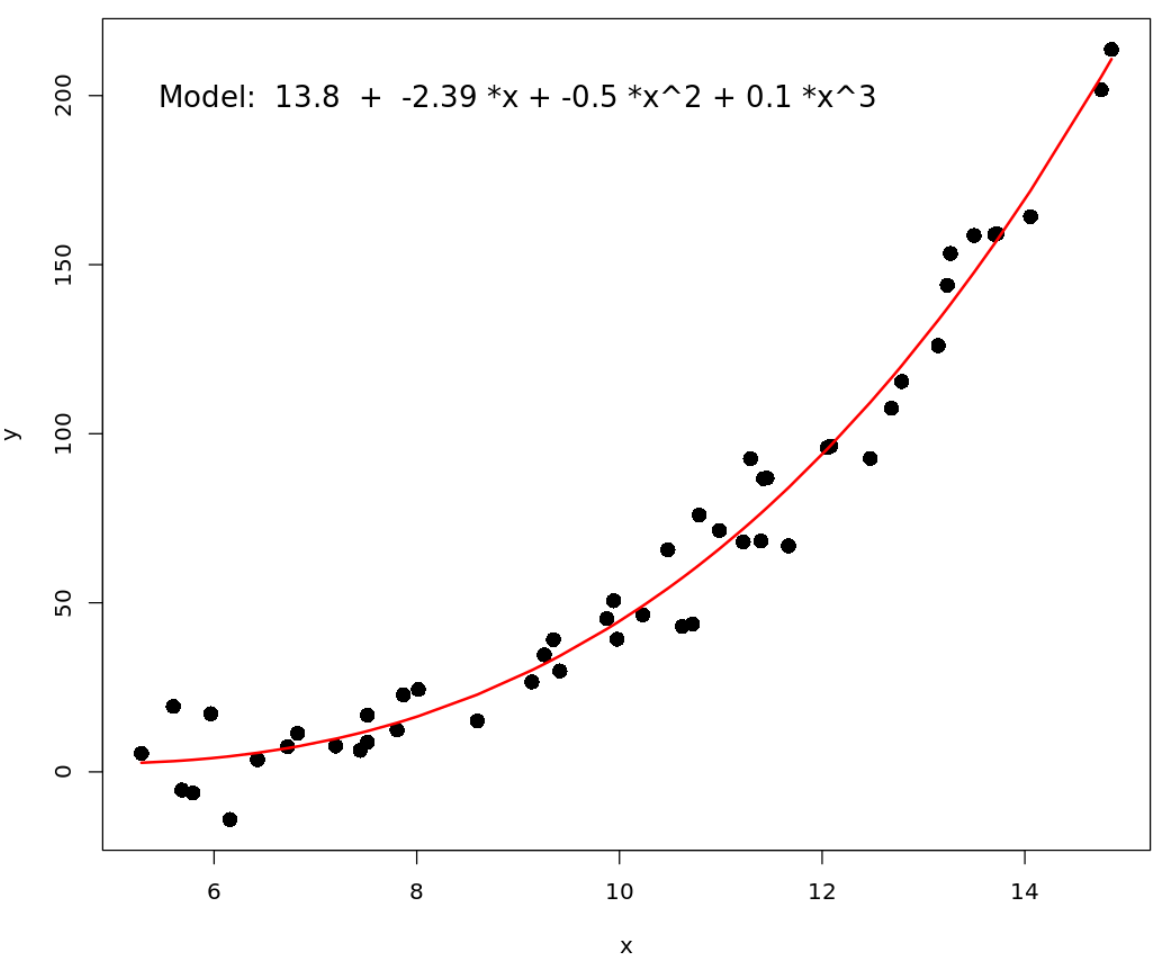
Обратите внимание, что аргумент cex управляет размером шрифта текста. По умолчанию установлено значение 1, поэтому мы решили использовать значение 1,3 , чтобы текст было легче читать.
Дополнительные ресурсы
Введение в полиномиальную регрессию
Как подогнать полиномиальную кривую в Excel
Как выполнить полиномиальную регрессию в Python