Почему важна статистика? (10 причин, почему статистика важна!)

Область статистики занимается сбором, анализом, интерпретацией и представлением данных.

Поскольку технологии все больше и больше проникают в нашу повседневную жизнь, генерируется и собирается больше данных, чем когда-либо прежде в истории человечества.

Статистика — это область, которая может помочь нам понять, как использовать эти данные для выполнения следующих задач:

• Лучше понять мир вокруг нас.
• Принимайте решения, используя данные.
• Делайте прогнозы о будущем, используя данные.

В этой статье мы поделимся 10 причинами, почему область статистики так важна в современной жизни.

Причина 1: Используйте описательную статистику, чтобы понять мир

Описательная статистика используется для описания фрагмента необработанных данных. Существует три основных типа описательной статистики:

• Сводные статистические данные
• Графика
• столы

Каждый из этих элементов может помочь нам лучше понять существующие данные.

Например, предположим, что у нас есть набор необработанных данных, показывающий результаты тестов 10 000 студентов в определенном городе. Мы можем использовать описательную статистику для:

• Рассчитайте средний балл теста и стандартное отклонение результатов теста.
• Создайте гистограмму или коробчатую диаграмму, чтобы визуализировать распределение результатов теста.
• Создайте таблицу частот, чтобы понять распределение результатов испытаний.

Используя описательную статистику, мы можем гораздо легче понять результаты тестов учащихся, чем просто глядя на необработанные данные.

Причина 2: Остерегайтесь вводящей в заблуждение графики

Все больше и больше графики создается в журналах, средствах массовой информации, онлайн-статьях и журналах. К сожалению, диаграммы часто могут вводить в заблуждение, если вы не понимаете лежащие в их основе данные.

Например, предположим, что журнал публикует исследование, в котором обнаруживается отрицательная корреляция между баллами GPA и ACT студентов определенного университета.

Однако эта отрицательная корреляция возникает только потому, что студенты, имеющие как высокий средний балл, так и ACT, могут поступать в элитный университет, в то время как студенты с низким средним баллом и ACT не принимаются вообще.

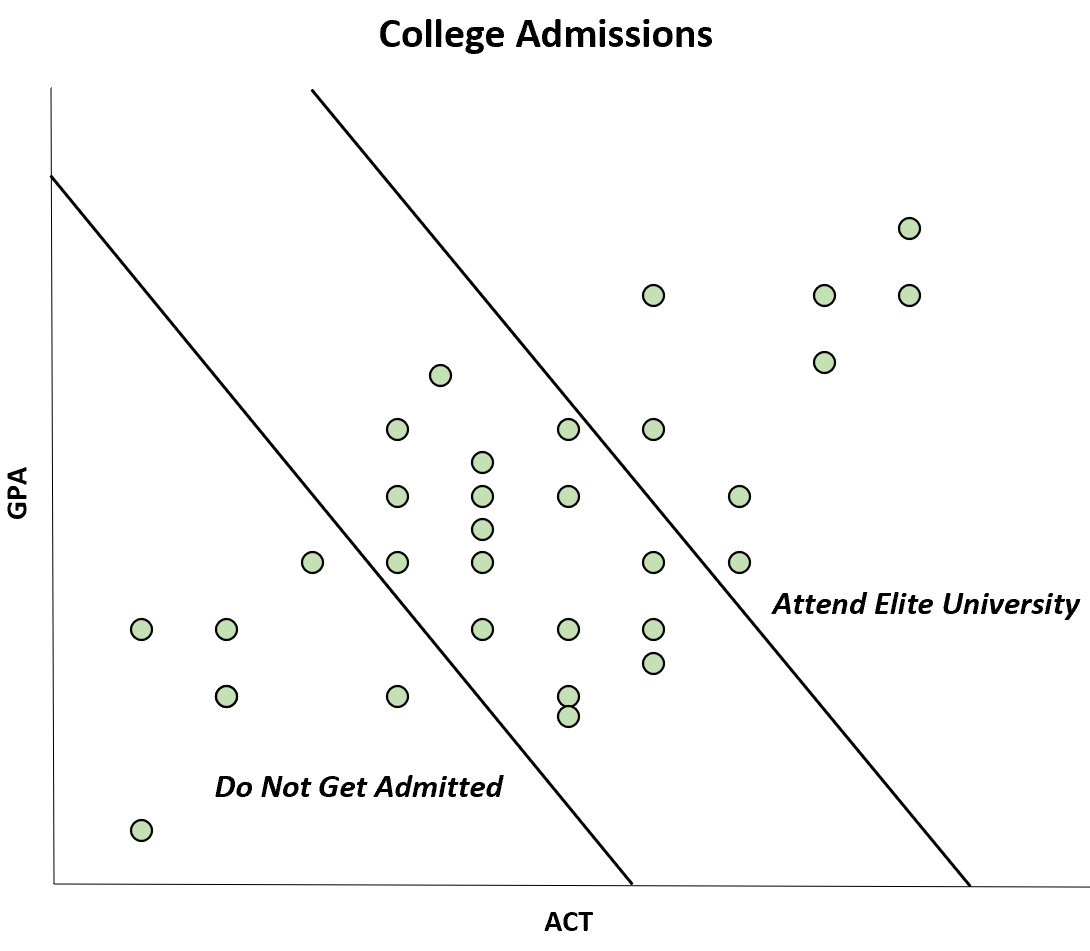
Хотя корреляция между ACT и GPA положительна в популяции, в выборке она оказывается отрицательной.

Эта конкретная предвзятость известна как предвзятость Берксона . Зная об этой предвзятости, вы можете избежать введения в заблуждение некоторыми графиками.

Причина 3: будьте осторожны, не путайте переменные

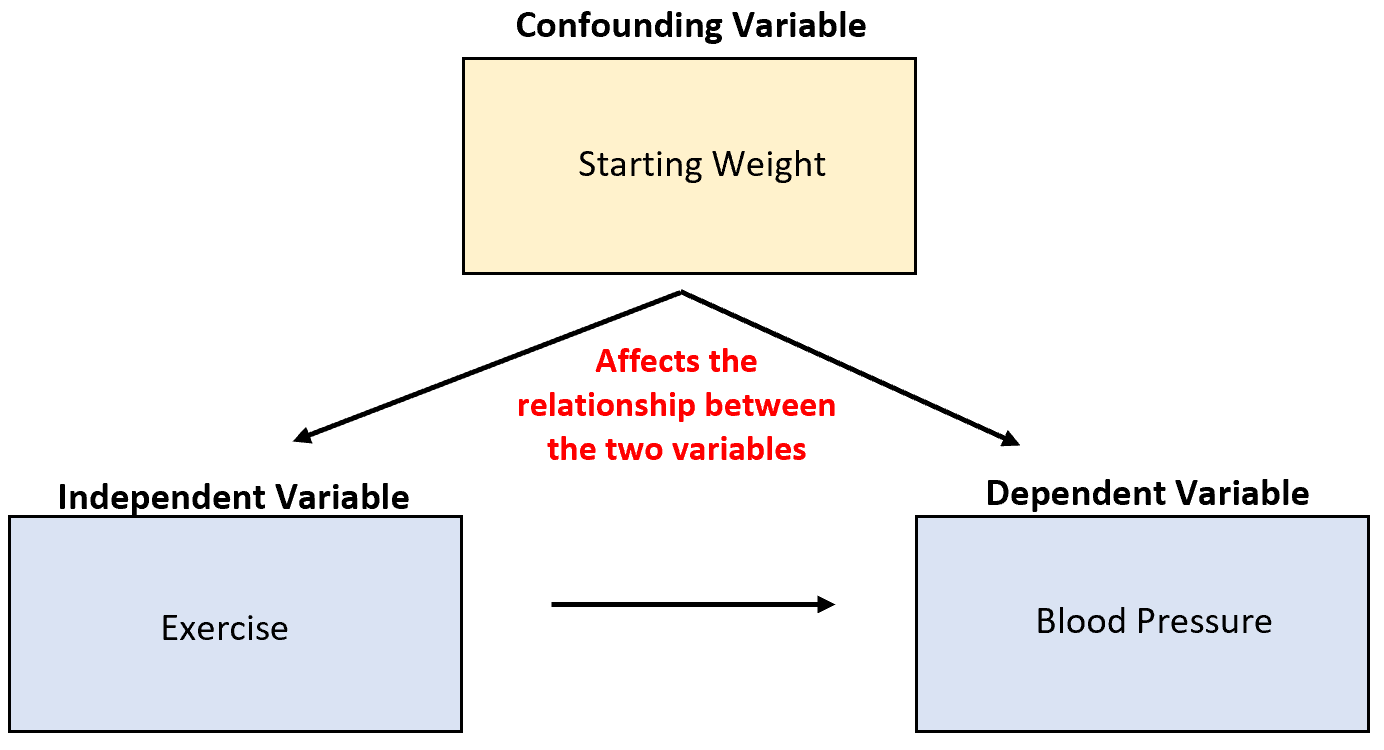
Важная концепция, о которой вы узнаете в статистике, — это концепция запутанных переменных .

Это переменные, которые не принимаются во внимание и могут исказить результаты эксперимента и привести к ненадежным выводам.

Например, предположим, что исследователь собирает данные о продажах мороженого и нападениях акул и обнаруживает, что эти две переменные тесно связаны. Означает ли это, что увеличение продаж мороженого приводит к увеличению количества нападений акул?

Это маловероятно. Наиболее вероятная причина — сбивающая с толку переменная температура . Когда на улице теплее, больше людей покупают мороженое и больше людей отправляются на океан.

Причина 4: принимать более обоснованные решения, используя вероятности

Одной из важнейших областей статистики является вероятность . Это область, которая изучает вероятность возникновения событий.

Имея базовое представление о вероятности, вы сможете принимать более обоснованные решения в реальном мире.

Например, предположим, что старшеклассник знает, что у него есть 10% шанс быть принятым в данный университет. Используя формулу вероятности прохождения «хотя бы одного» , этот студент может найти вероятность того, что его примут хотя бы в один университет, в который он подает документы, и может скорректировать количество университетов, в которые он подает документы, по результату.

Причина 5: Понимание P-значений в исследованиях

Еще одна важная концепция, о которой вы узнаете в статистике, — это p-значения .

Классическое определение p-значения:

Значение p — это вероятность наблюдения выборочной статистики, которая, по крайней мере, столь же экстремальна, как и ваша выборочная статистика, при условии, что нулевая гипотеза верна.

Например, предположим, что завод заявляет, что производит шины средним весом 200 фунтов. Аудитор предполагает, что фактический средний вес шин, произведенных на этом заводе, отличается на 200 фунтов. Итак, он выполняет проверку гипотезы и обнаруживает, что значение p теста составляет 0,04.

Вот как интерпретировать это значение p:

Если завод действительно производит шины средним весом 200 фунтов, то в 4% всех проверок будет достигнут эффект, наблюдаемый в выборке, и более из-за случайной ошибки выборки. Это говорит нам о том, что получение выборочных данных, полученных аудитором, было бы довольно редким явлением, если бы завод действительно производил шины средним весом 200 фунтов.

Таким образом, аудитор, скорее всего, отвергнет нулевую гипотезу о том, что фактический средний вес шин, производимых на этом заводе, действительно составляет 200 фунтов.

Причина 6: Поймите корреляцию

Еще одна важная концепция, о которой вы узнаете в статистике, — это корреляция , которая говорит нам о линейной связи между двумя переменными.

Значение коэффициента корреляции всегда находится в диапазоне от -1 до 1, где:

• -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
• 0 указывает на отсутствие линейной корреляции между двумя переменными.
• 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.

Поняв эти значения, вы сможете понять взаимосвязь между переменными в реальном мире.

Например, если корреляция между расходами на рекламу и доходами равна 0,87, то вы можете понять, что между этими двумя переменными существует сильная положительная связь. По мере того, как вы тратите больше денег на рекламу, вы можете ожидать предсказуемого увеличения доходов.

Причина 7: Делайте прогнозы на будущее

Еще одна важная причина изучать статистику — это понимание основных моделей регрессии, таких как:

• Простая линейная регрессия
• Множественная линейная регрессия
• Логистическая регрессия

Каждая из этих моделей позволяет делать прогнозы относительно будущего значения переменной ответа на основе значений определенных переменных-предсказателей в модели.

Например, компании постоянно используют множественные модели линейной регрессии в реальном мире, используя переменные-предикторы, такие как возраст, доход, этническая принадлежность и т. д. чтобы предсказать, сколько покупатели потратят в своих магазинах.

Аналогичным образом логистические компании используют прогнозные переменные, такие как общий спрос, численность населения и т. д. прогнозировать будущие продажи.

Независимо от того, в какой области вы работаете, есть большая вероятность, что регрессионные модели используются для прогнозирования будущего явления.

Причина 8: Понимание потенциальной систематической ошибки в исследованиях

Еще одна причина изучать статистику — это осознание всех различных типов предвзятости, которые могут возникнуть в реальных исследованиях.

Вот некоторые примеры:

• Соблюдайте предвзятость
• Предвзятость самоотбора
• Эталонное смещение
• Смещение пропущенной переменной
• Смещение занижения
• Систематическая ошибка в связи с отсутствием ответов

Имея базовое представление об этих типах предубеждений, вы можете избежать их совершения при проведении исследований или осознавать их при чтении других научных статей или исследований.

Причина 9: Понять предположения, сделанные статистическими тестами

Многие статистические тесты делают предположения относительно изучаемых данных.

Читая результаты исследования или даже проводя собственное исследование, важно понимать, какие предположения необходимо сделать, чтобы результаты были достоверными.

В следующих статьях представлены предположения, сделанные во многих широко используемых статистических тестах и процедурах:

• Что такое предположение о равной дисперсии в статистике?
• Что такое предположение нормальности в статистике?
• Что такое предположение независимости в статистике?

Причина 10: Чтобы избежать чрезмерных обобщений

Другая причина изучать статистику – это понимание концепции чрезмерного обобщения .

Это происходит, когда лица, участвующие в исследовании, не являются репрезентативными для лиц в общей популяции, и поэтому нецелесообразно обобщать результаты исследования на всю популяцию.

Например, предположим, что мы хотим знать, какой процент учеников определенной школы предпочитает «драму» своим любимым жанром кино. Если общая численность учащихся представляет собой смесь 50% мальчиков и 50% девочек, то выборка, состоящая из 90% мальчиков и 10% девочек, может привести к необъективным результатам, если значительно меньше мальчиков предпочитают театр как любимый жанр.

В идеале мы хотим, чтобы наша выборка напоминала «мини-версию» нашей популяции. Таким образом, если общая численность учащихся состоит из 50% девочек и 50% мальчиков, наша выборка не будет репрезентативной, если она будет включать 90% мальчиков и только 10% девочек.

Итак, независимо от того, проводите ли вы собственный опрос или читаете результаты опроса, важно понимать, являются ли данные выборки репрезентативными для всей совокупности и можно ли с уверенностью распространить результаты опроса на генеральную совокупность.

Дополнительные ресурсы

Прочтите следующие статьи, чтобы получить базовое представление о наиболее важных концепциях вводной статистики:

Описательная или косвенная статистика
Население против. образец
Статистика против параметров
Качественные и количественные переменные
Уровни измерения: номинальный, порядковый, интервальный и коэффициентный.