Почему стандартное отклонение важно? (пояснение + примеры)
Стандартное отклонение используется для измерения распределения значений в выборке.
Мы можем использовать следующую формулу для расчета стандартного отклонения данной выборки:
√ Σ(x i – x bar ) 2 / (n-1)
Золото:
- Σ: Символ, означающий «сумма».
- x i : i- е значение выборки
- x bar : Образец означает
- n: Размер выборки
Чем выше значение стандартного отклонения, тем более разбросаны значения в выборке. И наоборот, чем ниже значение стандартного отклонения, тем теснее кластеризуются значения.
Студенты часто задают вопрос: почему важно стандартное отклонение?
Ответ: Стандартное отклонение важно, потому что оно говорит нам о распределении значений в данном наборе данных.
мы анализируем набор данных Всякий раз, когда мы хотим найти следующие показатели:
- Центр набора данных . Самый распространенный способ измерения «центра» — использование среднего значения и медианы.
- Распределение значений в наборе данных . Самый распространенный способ измерения спреда — использование стандартного отклонения.
Зная, где находится центр и каково распределение значений, мы можем хорошо понять распределение значений в любом наборе данных.
Следующие примеры иллюстрируют важность стандартного отклонения на практике.
Пример 1: Распределение заработной платы
Предположим, что средняя зарплата в компании А составляет 80 000 долларов, а стандартное отклонение — 20 000 долларов. Поскольку стандартное отклонение настолько велико, нет никакой гарантии, что вам будут платить около 80 000 долларов в год, если вы будете работать в этой компании, потому что зарплаты очень сильно различаются.
И наоборот, предположим, что средняя зарплата в компании B также составляет 80 000 долларов, но стандартное отклонение составляет всего 4 000 долларов. Поскольку это стандартное отклонение настолько мало, вы можете быть уверены, что вам заплатят около 80 000 долларов, поскольку различия в зарплатах очень незначительны.
Если бы мы создали коробчатую диаграмму для визуализации распределения заработной платы в этих двух компаниях, она могла бы выглядеть так:
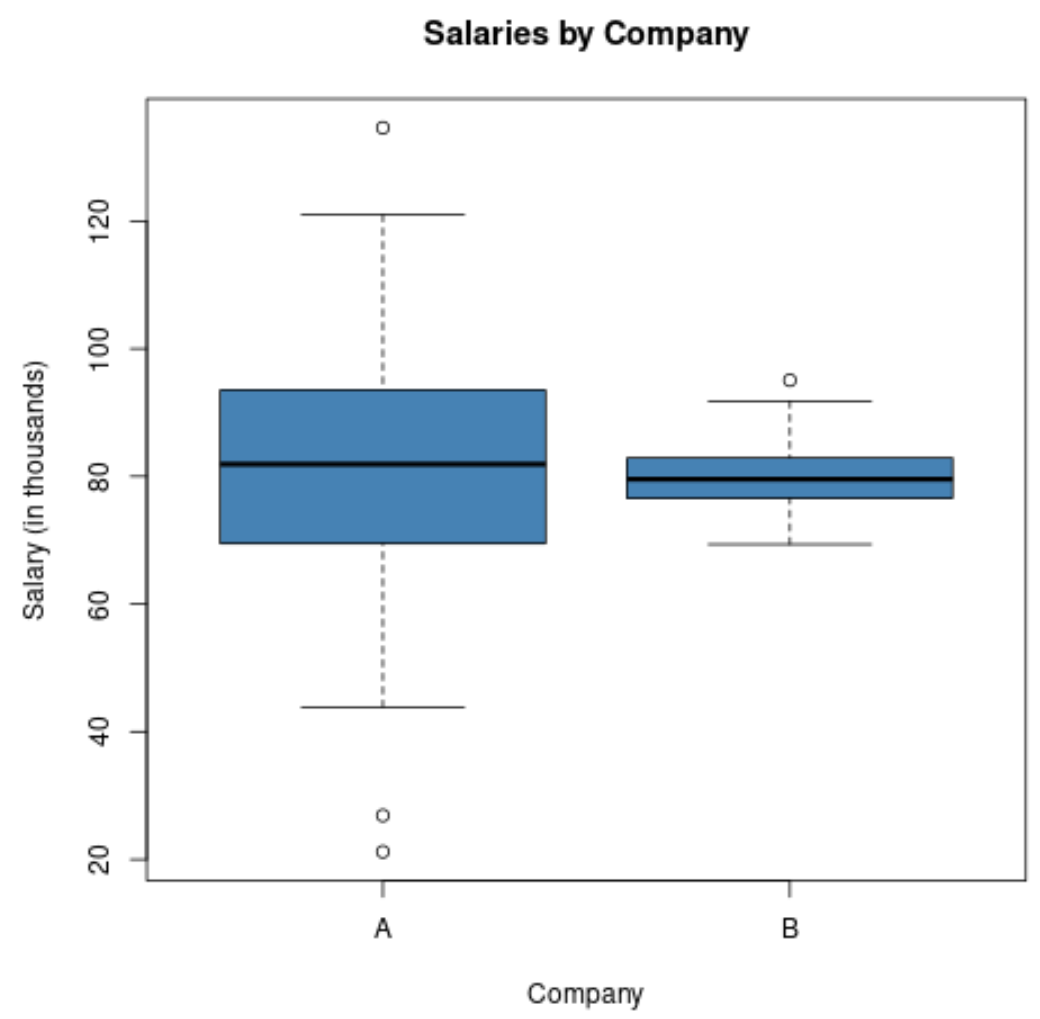
Обратите внимание, что длина коробчатой диаграммы для компании А больше, поскольку стандартное отклонение заработной платы намного выше.
Обе компании имеют одинаковую среднюю зарплату, но в компании А разница в зарплатах намного выше.
Пример 2: Распределение цен на жилье
Предположим, что средняя цена на жилье в районе А составляет 250 000 долларов, а стандартное отклонение — 50 000 долларов. Поскольку стандартное отклонение довольно велико, это означает, что цены на некоторые дома будут намного выше 250 000 долларов, а другие будут намного ниже. Если вы посмотрите на любой дом в этом районе, нет никакой гарантии, что цена будет хоть сколько-нибудь близкой к средней.
И наоборот, предположим, что средняя цена дома в районе B также составляет 250 000 долларов, но стандартное отклонение составляет всего 10 000 долларов. Поскольку это стандартное отклонение довольно мало, вы можете быть уверены, что любой дом по соседству, на который вы посмотрите, скорее всего, будет закрыт по этой цене.
Если бы мы создали коробчатую диаграмму для визуализации распределения цен на жилье в этих двух районах, она могла бы выглядеть так:
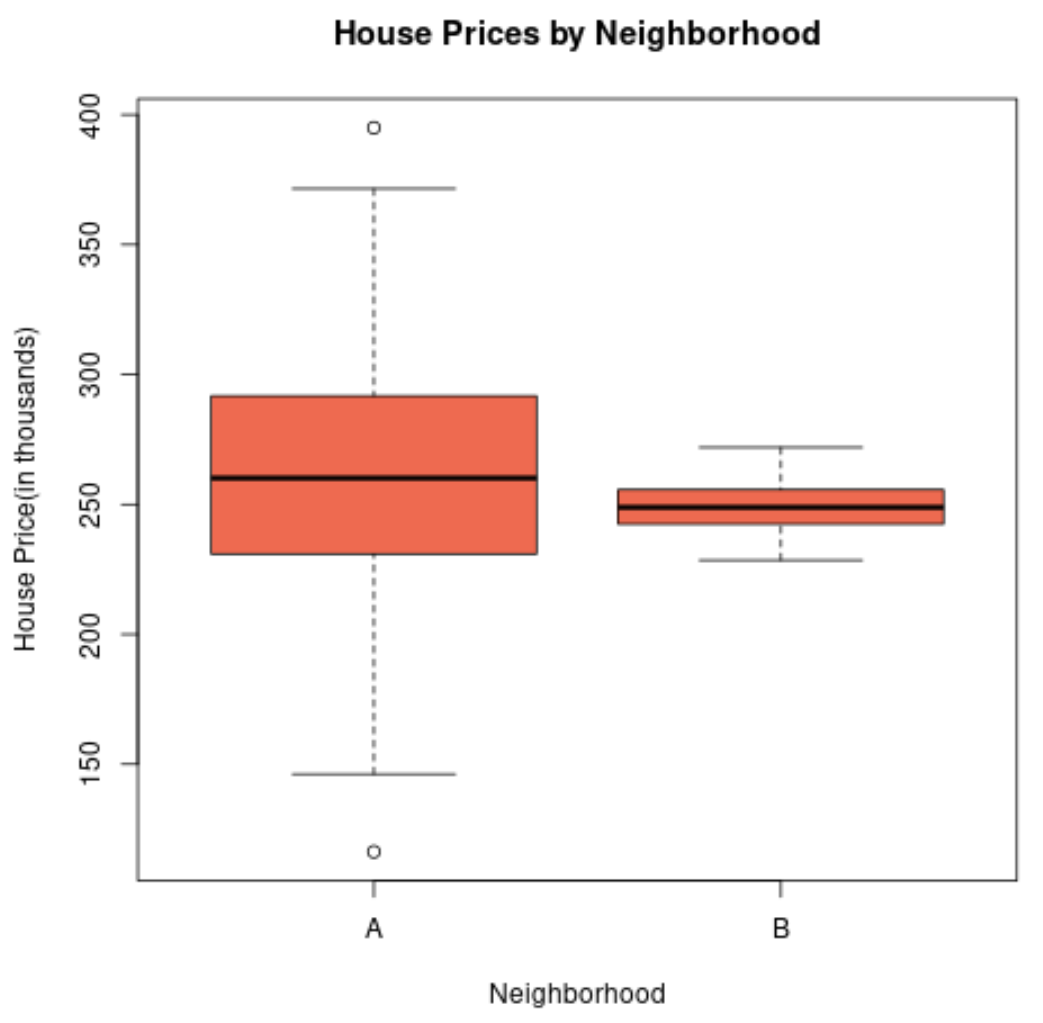
Длина коробчатого графика района А больше, поскольку стандартное отклонение цен на недвижимость намного выше.
Фактически, цены на жилье варьируются от менее 150 000 до более 400 000 долларов для района А, тогда как цены колеблются только от 230 000 до 270 000 долларов для района Б.
Просто зная стандартное отклонение цен на жилье в каждом районе, мы можем знать, насколько сильного изменения цен следует ожидать в каждом районе.
Дополнительные ресурсы
Что считается хорошим стандартным отклонением?
Диапазон против. Стандартное отклонение: когда использовать каждое
Коэффициент вариации против стандартного отклонения: разница