Как выполнить пошаговую регрессию в sas (с примером)
Пошаговая регрессия — это процедура, которую мы можем использовать для построения модели регрессии из набора переменных-предикторов путем поэтапного ввода и удаления предикторов в модели до тех пор, пока не исчезнет статистически обоснованная причина для ввода или удаления предикторов. удалить еще.
Целью пошаговой регрессии является создание модели регрессии, включающей все переменные-предикторы, которые статистически значимо связаны с переменной ответа .
Чтобы выполнить пошаговую регрессию в SAS, вы можете использовать PROC REG с оператором SELECTION .
В следующем примере показано, как на практике выполнить пошаговую регрессию в SAS.
Пример: выполнение пошаговой регрессии в SAS
Предположим, у нас есть следующий набор данных в SAS, который содержит четыре переменные-предикторы (x1, x2, x3, x4) и одну переменную ответа (y):
/*create dataset*/ data my_data; input x1 x2 x3 x4 y; datalines ; 1 4 10 13 78 2 4 12 14 81 5 3 7 10 75 8 2 13 9 97 10 5 12 5 95 14 7 8 6 90 17 8 10 6 86 19 5 15 5 90 20 5 12 4 93 21 4 10 3 95 ; run ; /*view dataset*/ proc print data =my_data;
Теперь предположим, что мы хотим определить, какая комбинация переменных-предикторов создаст лучшую модель множественной линейной регрессии .
Когда мы говорим о «лучшей» регрессионной модели, мы имеем в виду модель, которая максимизирует или минимизирует определенные показатели.
Есть две метрики, которые мы обычно используем для оценки того, какая модель регрессии является лучшей среди группы потенциальных моделей:
1. Скорректированный R-квадрат . Скорректированное значение R-квадрата говорит нам о полезности модели, скорректированной на основе количества предикторов в модели. Модель с наибольшим скорректированным значением R-квадрата считается лучшей.
2. AIC : Информационный критерий Акаике (AIC) — это показатель, используемый для сравнения соответствия различных моделей регрессии. Модель с наименьшим значением AIC считается лучшей.
К счастью, мы можем вычислить как подобранные значения R-квадрата, так и значения AIC для регрессионных моделей в SAS, используя PROC REG с оператором SELECTION .
Следующий код показывает, как это сделать:
/*perform stepwise multiple linear regression*/ proc reg data =my_data outest =est; model y=x1 x2 x3 x4 / selection=adjrsq aic ; output out =out p=pr=r; run ; quit ;
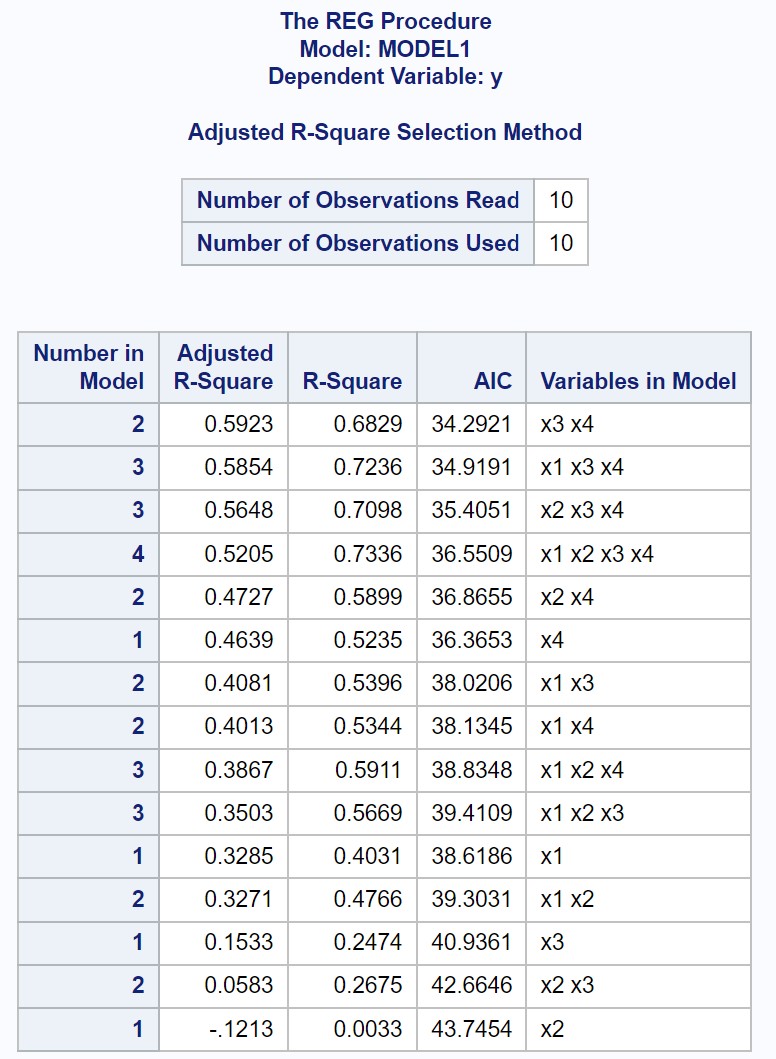
На выходе отображаются подобранные значения R-квадрата и AIC для каждой возможной модели множественной линейной регрессии.
Из результата мы видим, что значение с самым высоким скорректированным значением R-квадрата и самым низким значением AIC представляет собой регрессионную модель, которая использует только x3 и x4 в качестве переменных-предикторов.
Таким образом, мы заявляем, что следующая модель является «лучшей» среди всех возможных моделей:
у = б 0 + б 1 (х3) + б 2 (х4)
Эта конкретная регрессионная модель имеет следующие показатели:
- Скорректированное значение R-квадрата: 0,5923.
- АИК: 34.2921
Примечания по выбору «лучшей» регрессионной модели
Обратите внимание, что иногда модель с самым высоким скорректированным значением R-квадрата не всегда также имеет самое низкое значение AIC.
Когда дело доходит до принятия решения о том, какая модель регрессии лучше, в качестве рекомендаций можно использовать скорректированные R-квадрат и AIC, но в реальном мире вам может потребоваться использовать опыт в предметной области, чтобы определить, какая модель является лучшей.
Также может быть разумным выбратьэкономную модель , то есть модель, которая достигает желаемого уровня соответствия, используя как можно меньше переменных-предикторов.
Обоснование модели этого типа проистекает из идеи бритвы Оккама (иногда называемой «принципом экономности»), которая гласит, что самое простое объяснение, вероятно, является правильным.
Применительно к статистике, модель, которая имеет мало параметров, но достигает удовлетворительного уровня соответствия, должна быть предпочтительнее модели, которая имеет массу параметров и достигает лишь немного более высокого уровня соответствия.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в SAS:
Как выполнить простую линейную регрессию в SAS
Как выполнить множественную линейную регрессию в SAS
Как выполнить полиномиальную регрессию в SAS
Как выполнить логистическую регрессию в SAS