Правило сложения (или правило сложения)

К бенджамин андерсон 1 августа, 2023 Вероятность 0 комментариев

В этой статье объясняется, что такое правило сложения, также известное как правило сложения, и для чего оно используется в теории вероятности и статистике. Кроме того, вы сможете увидеть, что представляет собой формула правила сложения, и решить упражнения, показывающие, как ее использовать.

Что такое правило сложения (или правило сложения)?

Правило сложения (или правило сложения ) гласит, что сумма вероятностей двух событий равна сумме вероятностей каждого события, происходящего отдельно, минус вероятность того, что оба события произойдут одновременно.

Следовательно, формула правила сложения: P(A⋃B)=P(A)+P(B)−P(A⋂B).

Таким образом, чтобы сложить две вероятности, мы не можем просто сложить каждую вероятность, поскольку мы должны также вычесть член, который представляет собой совместную вероятность двух событий. Однако в некоторых случаях, только сложив вероятности каждого события, можно получить правильный результат суммы вероятностей. Ниже мы увидим, что это за случаи.

Короче говоря, правило сложения используется для расчета вероятности возникновения того или иного события, то есть вероятности того, что произойдет хотя бы одно из двух возможных событий.

Формула правила сложения

Правило сложения гласит, что для расчета вероятности возникновения события A или события B мы должны сложить вероятность возникновения события A плюс вероятность возникновения события B и вычесть вероятность того, что оба события произойдут одновременно. .

Таким образом , формула правила сложения (или правила сложения) выглядит следующим образом:

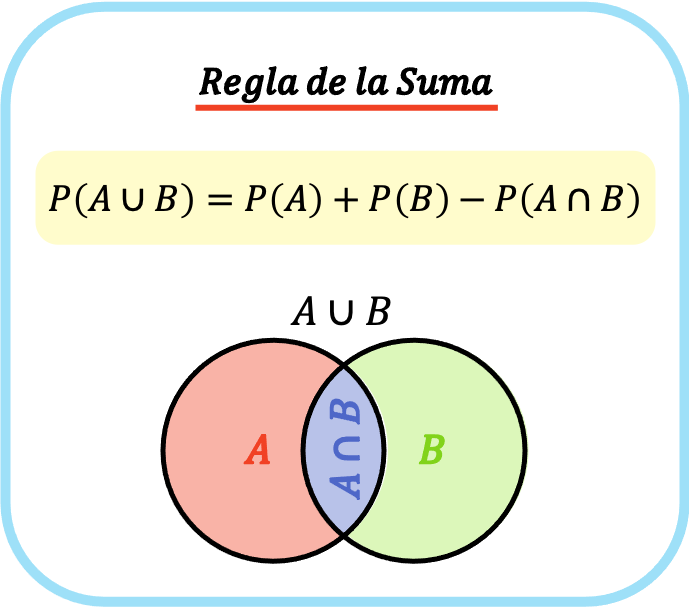
формула правила сложения, формула правила сложения

Золото:

$P(A\cup B)$

— вероятность события А или события Б.
$P(A)$

вероятность того, что событие А произойдет.
$P(B)$

— вероятность того, что событие B произойдет.
$P(A\cap B)$

— это совместная вероятность того, что событие A и событие B произойдут.

Следовательно, чтобы использовать правило сумм, вам необходимо знать, как рассчитать совместную вероятность двух событий. Посмотреть, как это делается, можно по следующей ссылке:

➤ См.: Как рассчитать совместную вероятность.

Пример правила сумм для эксклюзивных событий

Чтобы завершить понимание концепции, давайте рассмотрим пример применения правила сложения.

Положим в коробку 10 синих шаров, 6 оранжевых и 4 зеленых шара. Какова вероятность вытащить синий или оранжевый шар?

В упражнении нам предлагается определить вероятность того, что произойдет то или иное событие. Следовательно, для решения задачи нам необходимо воспользоваться формулой правила сложения:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Итак, сначала рассчитаем вероятность того, что каждое событие произойдет отдельно, используяправило Лапласа :

$P(\text{bola azul})=\cfrac{10}{10+6+4}=0,5$

$P(\text{bola naranja})=\cfrac{6}{10+6+4}=0,3$

Однако в этом случае оба события не могут произойти одновременно, поскольку это два взаимоисключающих события . То есть, если мы нарисуем синий шар, мы больше не сможем нарисовать оранжевый шар, и наоборот.

Следовательно, совместная вероятность обоих событий равна нулю, и, следовательно, формула правила сумм упрощается:

$P(A\cup B)=P(A)+P(B)-\cancelto{0}{P(A\cap B)}$

Итак, расчет вероятности поймать синий или оранжевый шарик следующий:

$\begin{aligned}P(\text{bola azul}\cup \text{bola naranja})&=P(\text{bola azul})+P(\text{bola azul})\\[2ex]&=0,5+0,3\\[2ex]&=0,8\end{aligned}$

Короче говоря, вероятность вытащить из коробки синий или оранжевый шар составляет 80%.

Пример правила добавления для неэксклюзивных событий

Рассмотрев конкретный пример правила сложения, когда события эксклюзивны, мы теперь увидим, как этот закон используется, когда события неисключительны.

Если мы подбросим монету дважды, какова вероятность выпадения орла хотя бы при одном броске?

В данном случае события не являются взаимоисключающими, поскольку мы можем получить «орла» при первом выпадении и «решку» при втором. Таким образом, формула правила сложения не упрощается и выглядит следующим образом:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Итак, сначала нам нужно посчитать вероятность выпадения «орла» при подбрасывании монеты, применив правило Лапласа:

$P(\text{cara})=\cfrac{1}{2}=0,5$

Кроме того, эти два события независимы, поэтому мы можем вычислить совместную вероятность двух событий, используя правило произведения :

$P(\text{cara}\cap \text{cara})=\cfrac{1}{2}\cdot \cfrac{1}{2}=0,5\cdot 0,5=0,25$

Наконец, чтобы найти вероятность того, что хотя бы в одном из двух бросков выпадет решка, просто подставьте значения в формулу правила сложения и выполните расчет:

$\begin{aligned}P(\text{cara}\cup \text{cara})&=P(\text{cara})+P(\text{cara})-P(\text{cara}\cap \text{cara})\\[2ex]&=0,5+0,5-0,25\\[2ex]&=0,75\end{aligned}$

В заключение, вероятность того, что при двукратном подбрасывании монеты хотя бы один раз выпадет орел, составляет 75%.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше