Правило стерджеса

В этой статье объясняется, что такое правило Стерджеса и какова его формула. Вы также найдете пошаговый конкретный пример правила Стерджеса и, кроме того, онлайн-калькулятор правил Стерджеса.

Что такое правило Стерджеса?

Правило Стерджеса — это правило, используемое для расчета идеального количества классов или интервалов, на которые следует разделить набор данных.

Формула правила Стерджеса гласит, что количество классов равно одному плюс логарифм по основанию два от общего количества данных.

Золото

количество классов или интервалов и

— общее количество наблюдений в выборке.

Правило Стерджеса было создано в 1926 году немецким статистиком Гербертом Стерджесом.

Пример правила Стерджеса

Теперь, когда мы знаем, что такое правило Стерджеса, мы увидим, решая пошаговое упражнение, как интервалы набора данных рассчитываются с использованием правила Стерджеса в статистике.

• Был измерен размер выборки из 50 разных людей, и все значения были записаны в следующей таблице данных. Примените правило Стерджеса, чтобы разделить набор данных на интервалы, а затем нанести данные на гистограмму.

Во-первых, нам нужно разделить данные на интервалы. Всего имеется 50 элементов данных, поэтому мы используем правило Стерджеса с этим значением:

Поэтому необходимо разделить данные и сгруппировать их по семи интервалам. Теперь нам нужно знать ширину каждого интервала, для этого просто разделите максимальное значение минус минимальное значение на общее количество интервалов:

Короче говоря, должно быть 7 интервалов с амплитудой 9, поэтому интервалы, рассчитанные по методу Стерджеса, таковы:

После того, как мы рассчитали интервалы, нам нужно посчитать, сколько раз фрагмент данных появляется в каждом интервале, и построить таблицу частот:

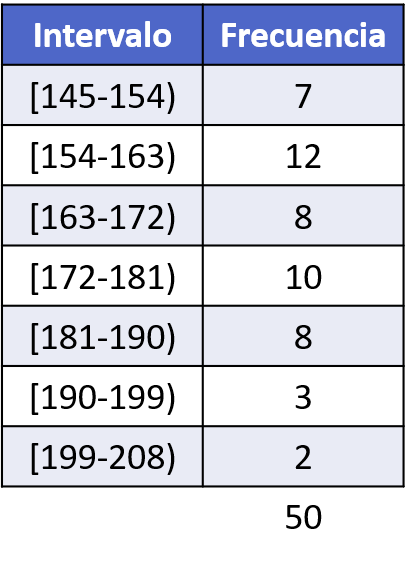
Наконец, из таблицы частот мы можем создать гистограмму для отображения данных:

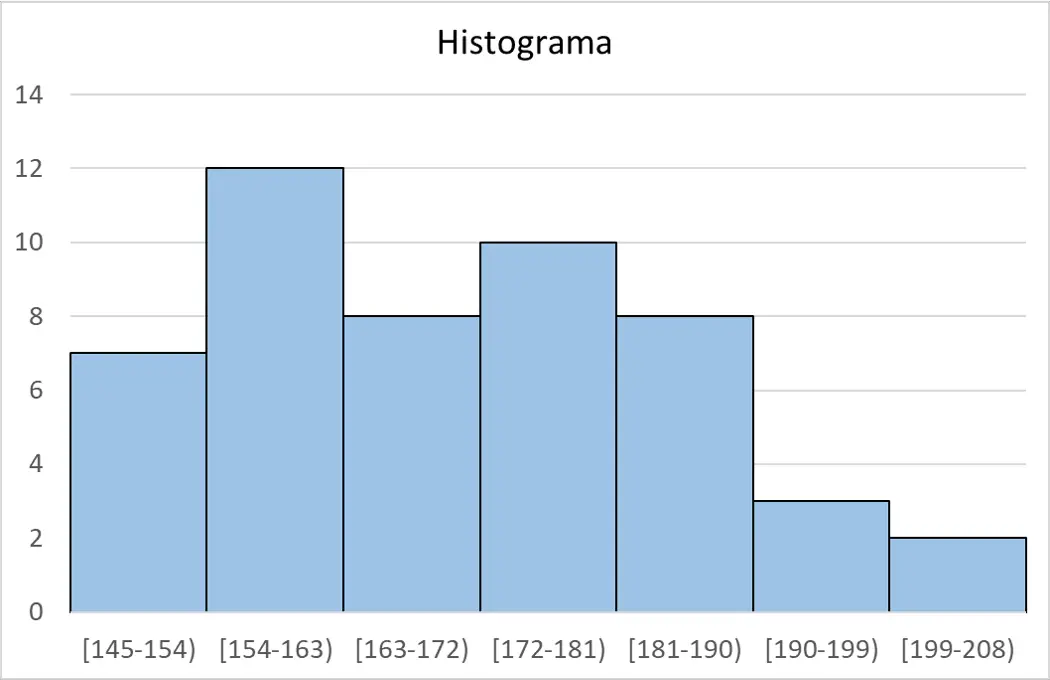
Калькулятор правил Стерджеса

Введите общее количество выборок данных и нажмите «Рассчитать», после чего калькулятор вернет количество интервалов, рассчитанное по правилу Стерджеса.