Как выполнить преобразование бокса-кокса в r (с примерами)
Преобразование Бокса-Кокса — это широко используемый метод преобразования набора данных с ненормальным распределением в набор с более нормальным распределением .
Основная идея этого метода состоит в том, чтобы найти такое значение λ, чтобы преобразованные данные были как можно ближе к нормальному распределению, используя следующую формулу:
- y(λ) = (y λ – 1)/λ, если y ≠ 0
- y(λ) = log(y), если y = 0
Мы можем выполнить преобразование box-cox в R, используя функцию boxcox() из библиотеки MASS() . В следующем примере показано, как использовать эту функцию на практике.
Обратитесь к этой статье из Университета Коннектикута, чтобы получить подробное описание разработки преобразования Бокса-Кокса.
Пример: преобразование Бокса-Кокса в R
В следующем коде показано, как подогнать модель линейной регрессии к набору данных, а затем использовать функцию boxcox() , чтобы найти оптимальную лямбду для преобразования переменной ответа и соответствия новой модели.
library (MASS) #create data y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8) x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8) #fit linear regression model model <- lm(y~x) #find optimal lambda for Box-Cox transformation bc <- boxcox(y ~ x) (lambda <- bc$x[which.max(bc$y)]) [1] -0.4242424 #fit new linear regression model using the Box-Cox transformation new_model <- lm(((y^lambda-1)/lambda) ~ x)
Оптимальная лямбда оказалась равна -0,4242424 . Таким образом, новая модель регрессии заменила исходную переменную ответа y на переменную y = (y -0,4242424 – 1)/-0,4242424.
Следующий код показывает, как создать два графика QQ в R для визуализации различий в остатках между двумя моделями регрессии:
#define plotting area op <- par(pty = "s", mfrow = c(1, 2)) #QQ plot for original model qqnorm(model$residuals) qqline(model$residuals) #QQ plot for Box-Cox transformed model qqnorm(new_model$residuals) qqline(new_model$residuals) #display both QQ plots by(op)
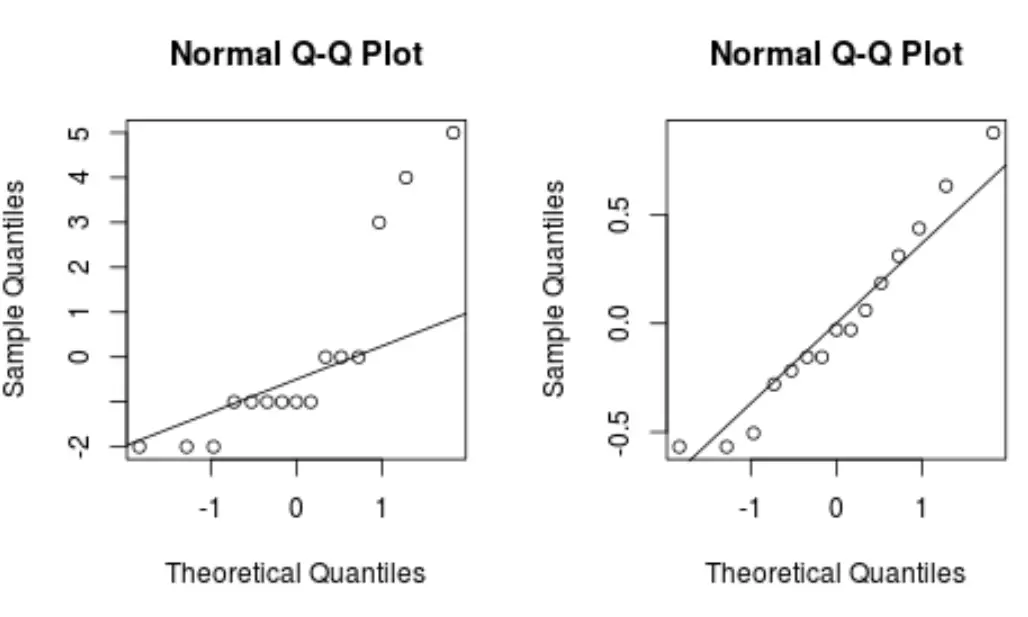
Как правило, если точки данных лежат вдоль прямой диагональной линии на графике QQ, набор данных, скорее всего, соответствует нормальному распределению.
Обратите внимание, как преобразованная модель Box-Cox создает график QQ с гораздо более прямой линией, чем исходная модель регрессии.
Это указывает на то, что остатки модели, преобразованной Бокс-Коксом, распределяются гораздо более нормально, что удовлетворяет одному из предположений линейной регрессии .
Дополнительные ресурсы
Как преобразовать данные в R (логарифм, квадратный корень, кубический корень)
Как создать и интерпретировать график QQ в R
Как выполнить тест Шапиро-Уилка на нормальность в R