5 примеров нелинейных связей между переменными

На большинстве курсов по статистике студенты узнают о линейных связях между переменными.

Это отношения, в которых увеличение одной переменной связано с предсказуемым увеличением другой переменной.

Примером этого может быть количество минут, сыгранных в баскетбольном матче, по сравнению с общим количеством набранных очков:

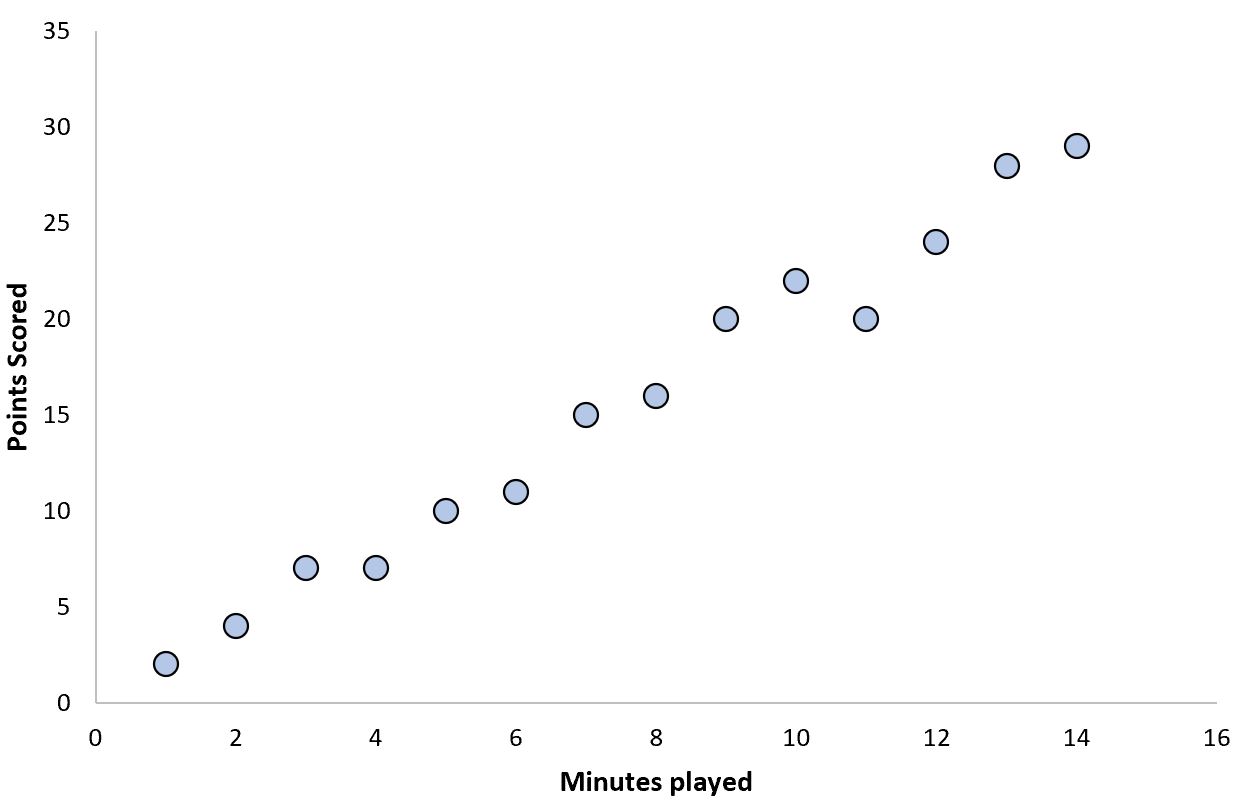
Игроки, которые играют больше минут, как правило, набирают больше очков.

Однако между переменными также могут быть нелинейные связи , которые постоянно возникают в реальном мире.

В этом руководстве представлены пять примеров нелинейных связей между переменными в реальном мире.

Пример 1: Квадратичные отношения

Одной из наиболее распространенных нелинейных связей в реальном мире является квадратичная зависимость между переменными.

При построении диаграммы рассеяния эта зависимость обычно имеет U-образную форму.

Примером может служить общее количество рабочих часов в неделю по сравнению с общим уровнем счастья:

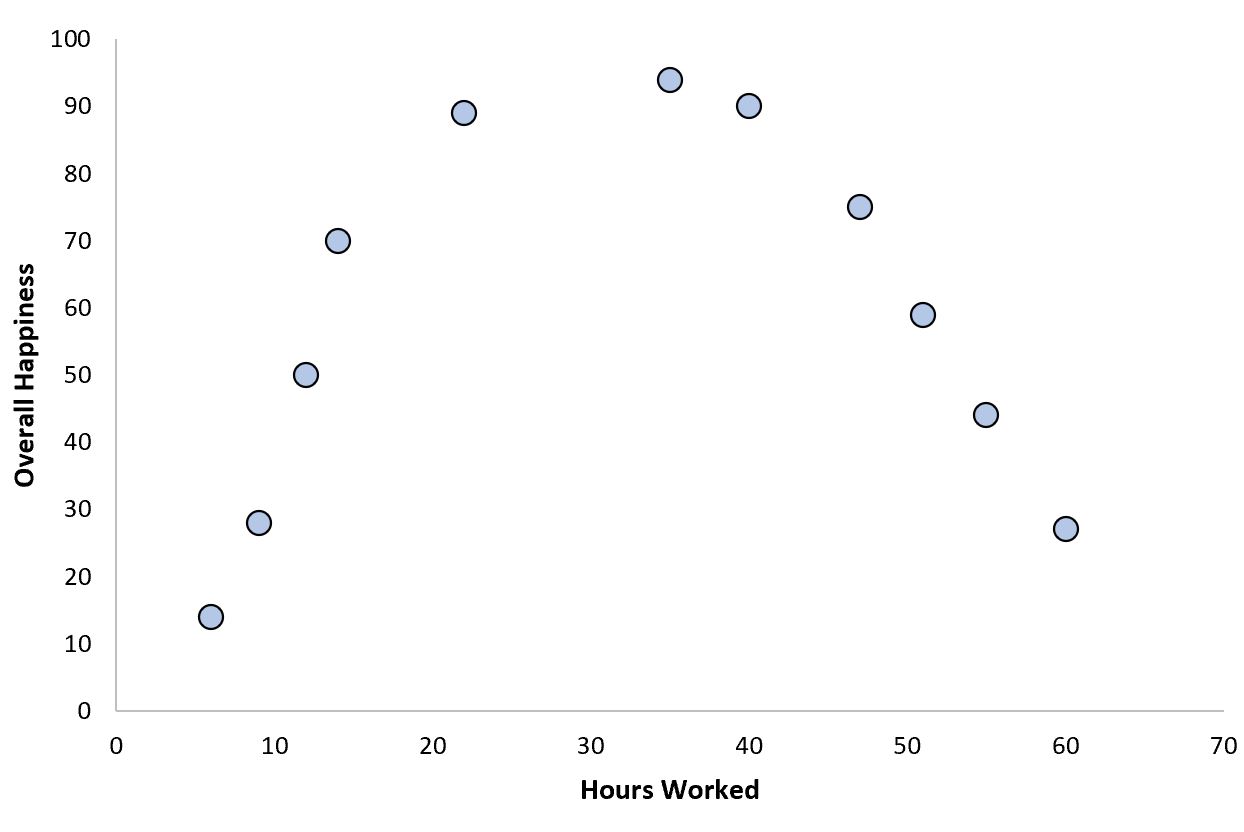
По мере того, как количество рабочих часов увеличивается с нуля, общее счастье имеет тенденцию к увеличению, но за пределами определенного порога увеличение количества рабочих часов фактически приводит к уменьшению счастья.

Эта перевернутая буква «U» является характерной формой квадратичной зависимости между двумя переменными.

Пример 2: Кубические отношения

Еще одна нелинейная зависимость, распространенная в реальном мире, — это кубическая зависимость между переменными.

При построении диаграммы рассеяния эта зависимость обычно показывает две отдельные кривые.

Этот тип отношений часто существует между переменными в области термодинамики:

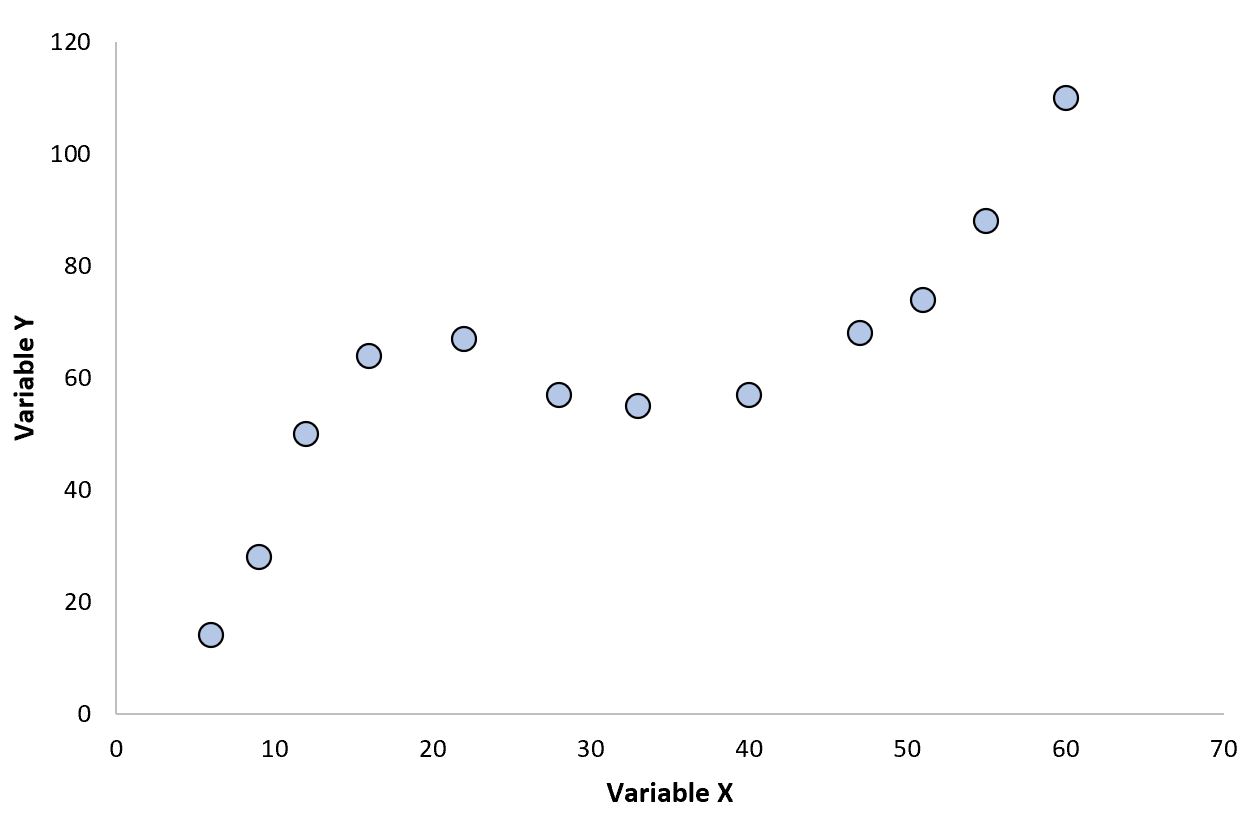
Обратите внимание, что на графике есть две отдельные кривые и что связь между переменной X и переменной Y явно не линейна.

Пример 3: Экспоненциальные отношения

Еще одна нелинейная зависимость, распространенная в реальном мире, — это экспоненциальная связь между переменными.

При нанесении на диаграмму рассеяния эта зависимость представляет собой уникальную кривую, которая становится более выраженной по мере увеличения переменной на оси X.

Хорошо известным примером показательной зависимости является продолжительность жизни бамбуковых растений и их годовой прирост:

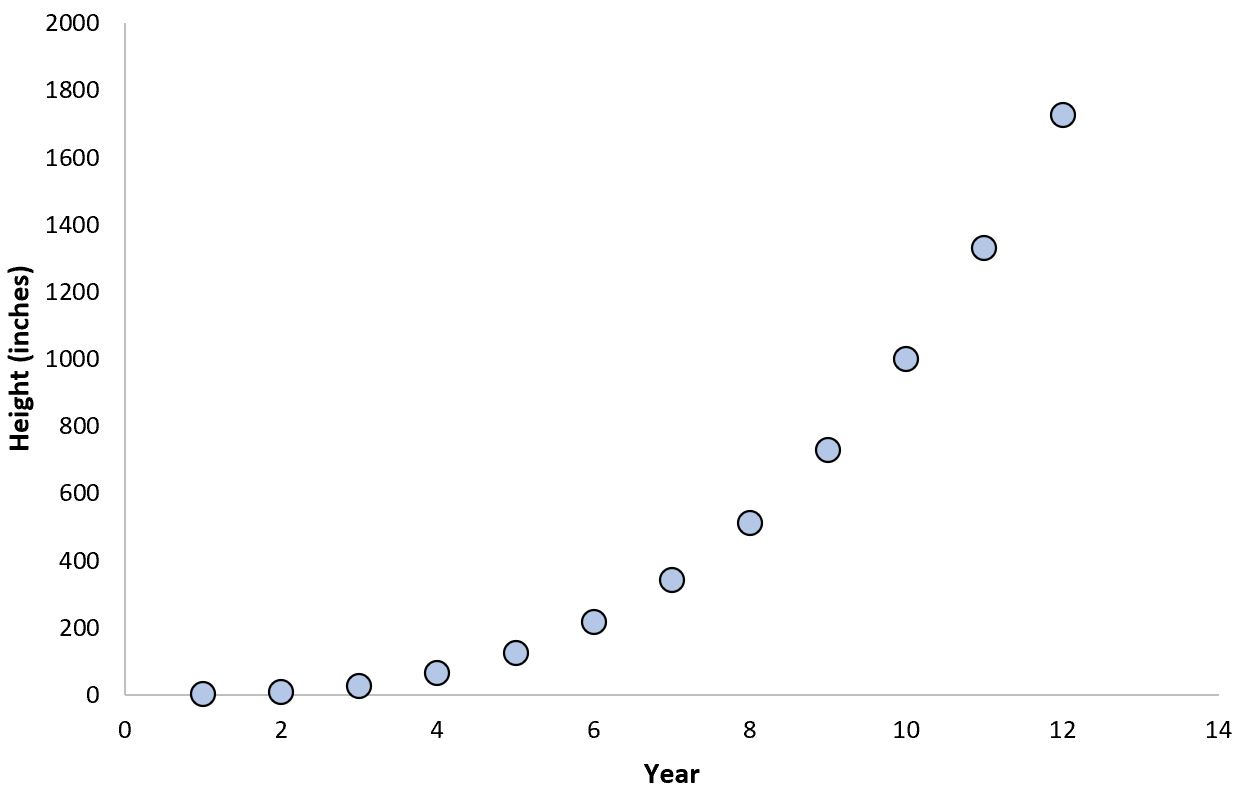
В течение первых нескольких лет роста бамбук растет очень медленно, но по достижении определенного возраста он резко увеличивается в высоту и растет быстрыми темпами.

Пример 4: Логарифмические отношения

Еще одна нелинейная зависимость, распространенная в реальном мире, — это логарифмическая связь между переменными.

При нанесении на диаграмму рассеяния эта зависимость представляет собой уникальную кривую, которая становится менее выраженной по мере увеличения переменной на оси X.

Примером логарифмической зависимости является зависимость между эффективностью технологий умного дома и временем:

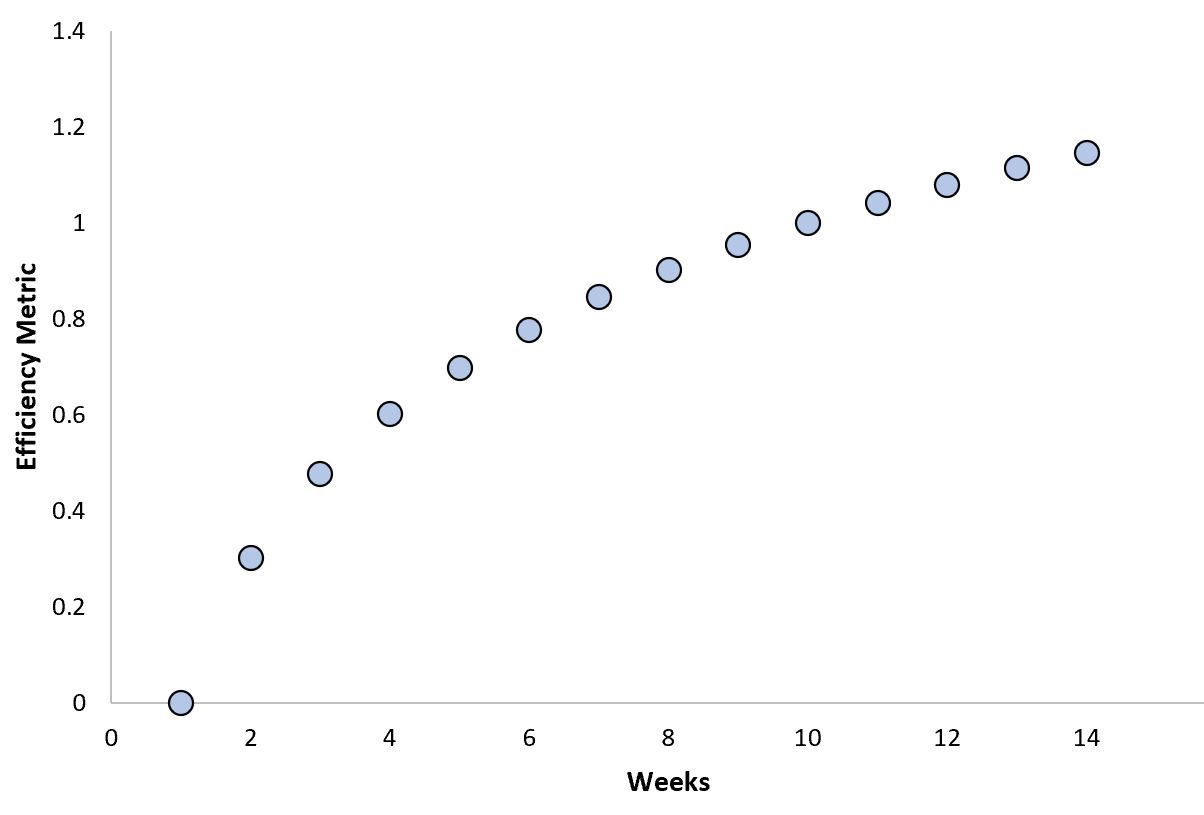
Когда в доме устанавливается новая технология умного дома (например, пылесос или автономный кондиционер), она быстро учится тому, как стать более эффективной, но как только она достигает определенной точки, она достигает максимального порога эффективности.

Пример 5: Косинусные отношения

Еще одна нелинейная зависимость, распространенная в реальном мире, — это косинусная связь между переменными.

При построении диаграммы рассеяния эта зависимость имеет «волновую» форму.

Примером косинусной зависимости является зависимость между частотой звуковых волн и временем:

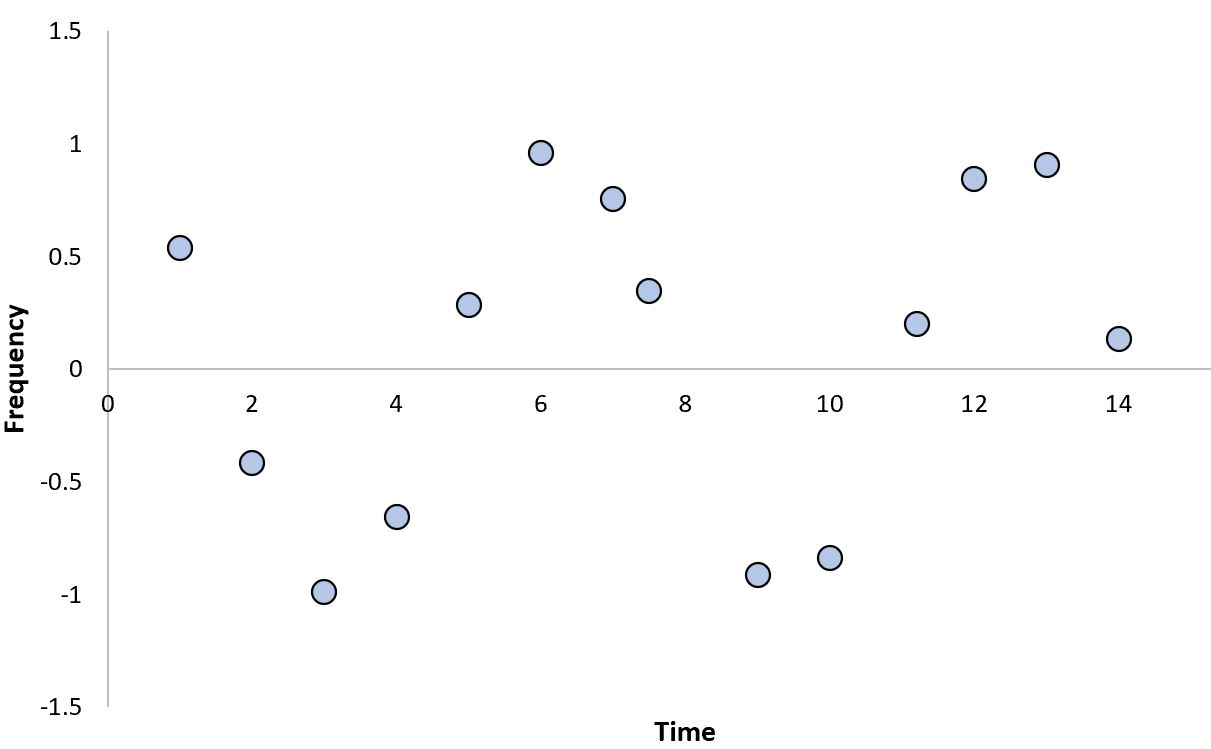
Обратите внимание, что зависимость имеет «волновую» форму, которая очень нелинейна.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять различные типы нелинейной регрессии в Excel:

Как выполнить квадратичную регрессию в Excel
Как выполнить кубическую регрессию в Excel
Как выполнить экспоненциальную регрессию в Excel
Как выполнить логарифмическую регрессию в Excel