Проблема монти холла: простое наглядное объяснение

В старом игровом шоу под названием «Давай заключим сделку » ведущий Монти Холл подарил участникам три двери.

В одной из дверей был приз, а в двух других — нет.

Монти просил участника выбрать, в какой двери, по его мнению, находится приз.

Как только участник выбирал дверь, Монти открывал дверь, в которой не было приза.

Приз остался в одной из двух закрытых дверей.

Затем Монти спрашивал кандидата, хотят ли они сменить дверь.

Хотя в это может показаться трудным поверить, оказывается, что смена дверей на этом этапе игры на самом деле дает вам больше шансов на победу.

Продолжайте читать, чтобы узнать, почему!

Визуальное объяснение проблемы Монти Холла

Чтобы проиллюстрировать, почему смена дверей увеличивает вероятность выигрыша, рассмотрим следующие сценарии, в которых вы сначала выбираете дверь 1.

Сценарий 1: Вы выбираете дверь 1, а приз на самом деле находится за дверью 1.

В этом случае Монти откроет дверь 2 или 3 и покажет вам, что за обеими дверьми ничего нет. Если вы останетесь у двери 1, вы выиграете .

Сценарий 2: Вы выбираете дверь 1, а приз фактически находится за дверью 2.

В этом случае Монти должен открыть дверь 3 и показать вам, что за ней ничего нет. Если вы останетесь у двери 1, вы проиграете .

Сценарий 3: Вы выбираете дверь 1, а приз фактически находится за дверью 3.

В этом случае Монти должен открыть дверь 2 и показать вам, что за ней ничего нет. Если вы останетесь у двери 1, вы проиграете .

Это все возможные результаты, если вы выберете дверь 1. Обратите внимание: если вы останетесь с дверью 1, вы сэкономите только треть времени. Но если вы поменяетесь, вы сэкономите две трети времени.

В следующей таблице суммированы все возможные сценарии этого игрового шоу, а также результаты, связанные с поддержанием и изменением:

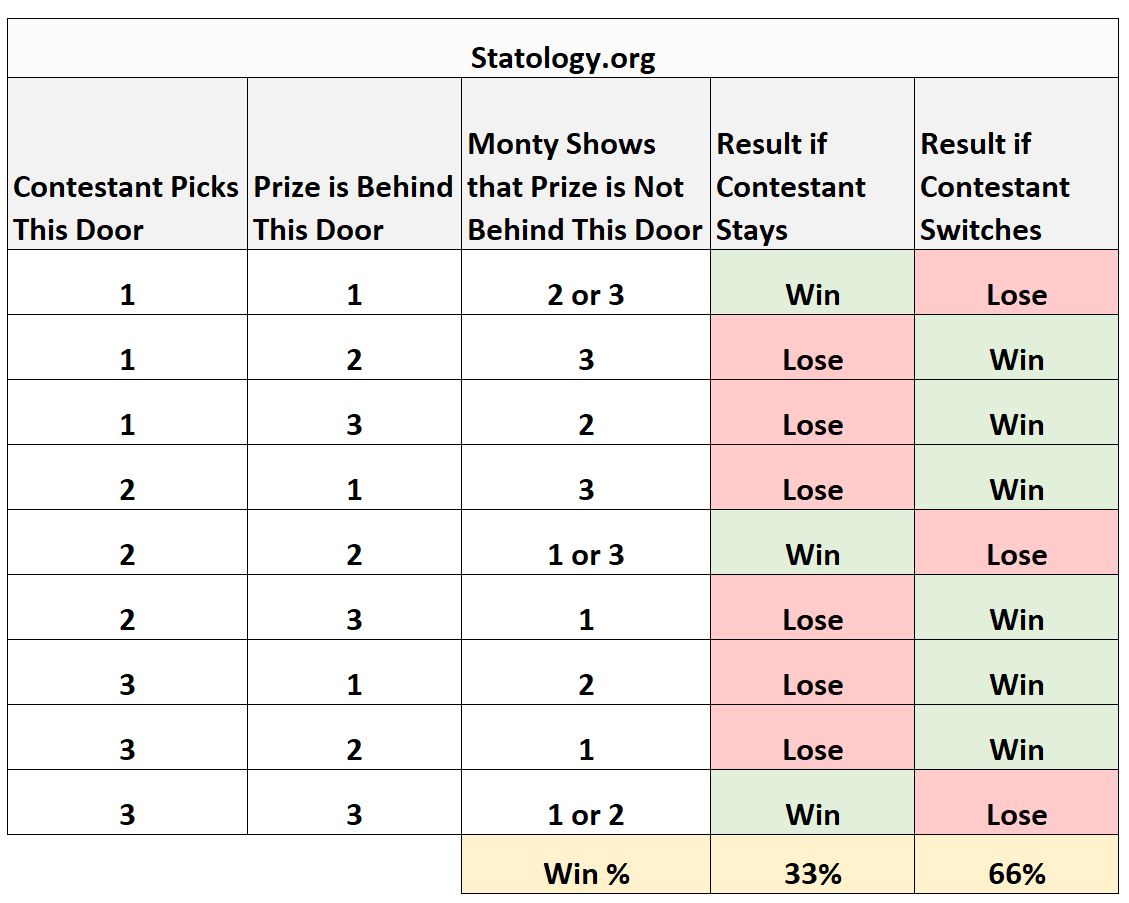
Из таблицы мы видим, что вы выигрываете в 33% случаев, когда остаетесь, но выигрываете в 66% случаев, когда переключаетесь.

Итак, смена дверей увеличивает вероятность того, что вы выиграете приз.

Хотя интуитивно это может показаться бессмысленным, математика не лжет.