Проверка гипотез на дисперсию

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое проверка гипотез на дисперсию. Итак, вы найдете формулу проверки дисперсионной гипотезы и, кроме того, пошаговое решение упражнения.

Что такое проверка гипотез на дисперсию?

Проверка гипотезы на дисперсию — это статистический метод, используемый для определения того, следует ли отвергать нулевую гипотезу дисперсии генеральной совокупности. Другими словами, проверка гипотезы дисперсии используется для отклонения или принятия гипотезы о значении дисперсии генеральной совокупности.

В частности, в зависимости от значения статистики проверки гипотезы на дисперсию и выбранного уровня значимости нулевая гипотеза отклоняется или принимается.

Имейте в виду, что проверка гипотез имеет много названий, ее также можно назвать контрастом гипотез, проверкой гипотез или проверкой значимости.

Формула проверки гипотез на дисперсию

Статистика проверки гипотезы на дисперсию равна разнице между размером выборки минус один раз выборочную дисперсию и деленной на предлагаемое значение генеральной дисперсии. Статистика проверки гипотезы на дисперсию имеет распределение хи-квадрат .

Таким образом, формула расчета статистики проверки гипотезы на дисперсию выглядит следующим образом:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Золото:

$\chi^2$

— это статистика проверки гипотезы на предмет дисперсии, которая имеет распределение хи-квадрат.
$n$

это размер выборки.
$s^2$

— выборочная дисперсия.
$\sigma^2$

— предполагаемая дисперсия генеральной совокупности.

Для интерпретации результата статистики полученное значение необходимо сравнить с критическим значением теста.

Если проверка гипотезы на дисперсию является двусторонней, нулевая гипотеза отклоняется, если статистика превышает критическое значение.
$\chi_{1-\alpha/2|n-1}^2$

или если критическое значение меньше

$\chi_{\alpha/2|n-1}$

.
Если проверка гипотезы на дисперсию соответствует правому хвосту, нулевая гипотеза отклоняется, если статистика превышает критическое значение.
$\chi_{1-\alpha|n-1}^2$

.
Если проверка гипотезы на дисперсию соответствует левому хвосту, нулевая гипотеза отклоняется, если статистика меньше критического значения.
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

Критические значения проверки гипотезы для дисперсии получаются из таблицы распределения хи-квадрат. Обратите внимание, что степени свободы распределения хи-квадрат равны размеру выборки минус 1.

Реальный пример проверки гипотез на дисперсию

Увидев определение проверки гипотезы дисперсии и ее формулу, мы увидим конкретный пример, позволяющий завершить усвоение этой концепции.

На заводе есть станок, который с высокой точностью производит детали для автомобилей. Однако есть подозрение, что оно отошло и теперь производит детали с зазором более 8 мм ² . Для опровержения этой гипотезы анализируется выборка из 25 штук, ее выборочная дисперсия составляет 9,1 мм ² . Можно ли отвергнуть исходную гипотезу при уровне значимости α=0,05?

Нулевая гипотеза и альтернативная гипотеза для этой проверки гипотезы дисперсии следующие:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}» title=»Rendered by QuickLaTeX.com» height=»65″ width=»101″ style=»vertical-align: 0px;»> Чтобы определить, можно ли отклонить нулевую гипотезу, мы вычисляем статистику проверки гипотезы для дисперсии, используя формулу, которую мы видели выше: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

Теперь мы ищем критическое значение, соответствующее правому хвосту для 24 степеней свободы и уровня значимости α = 0,05 в таблице распределения хи-квадрат:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

Таким образом, рассчитанная статистика меньше критического значения теста, и поэтому нулевая гипотеза теста гипотезы дисперсии не отклоняется, а отвергается альтернативная гипотеза.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ См.: Проверка гипотезы для среднего значения генеральной совокупности.
➤ См.: Проверка гипотезы относительно доли населения.

Проверка гипотезы на предмет дисперсии двух популяций

Проверка гипотезы дисперсии двух популяций используется для отклонения или принятия гипотезы о том, что дисперсии двух разных популяций равны.

Таким образом, нулевая гипотеза проверки гипотезы о дисперсии двух совокупностей всегда следующая:

$H_0: \sigma^2_1=\sigma^2_2$

Альтернативной гипотезой может быть один из трех вариантов:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

В этом случае формула для расчета статистики проверки гипотезы для дисперсии двух совокупностей имеет следующий вид:

$F=\cfrac{s_1^2}{s_2^2}$

Золото:

$F$

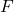
— это статистика проверки гипотезы для дисперсии двух популяций, которая соответствует распределению F.
$\sigma_1^2$

это дисперсия популяции 1.
$\sigma_2^2$

это дисперсия генеральной совокупности 2.
$s_1^2$

– это дисперсия выборки 1.
$s_2^2$

– это дисперсия выборки 2.
$n_1$

размер выборки 1.
$n_2$

размер выборки 2.

Поскольку распределение Snedecor F несимметрично, нулевая гипотеза отклоняется на основании следующих критериев:

[latex]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{черный} \ \text{Если }F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше