Проверка гипотезы на среднее значение

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое проверка гипотез на среднее значение в статистике. Таким образом, вы найдете формулу проверки гипотезы для среднего и, кроме того, пошагово решаемое упражнение.

Что такое проверка гипотезы на среднее значение?

Проверка гипотезы о среднем значении — это статистический метод, используемый для отклонения или отклонения нулевой гипотезы о среднем значении генеральной совокупности.

Более конкретно, проверка гипотезы на предмет среднего значения включает в себя расчет тестовой статистики и сравнение ее с критическим значением, позволяющим отвергнуть нулевую гипотезу или нет.

Следует отметить, что тесты гипотез имеют разные названия; в статистике их также называют контрастами гипотез, проверкой гипотез или проверкой значимости.

Формула проверки гипотезы для среднего значения

Далее мы увидим, как рассчитывается статистика проверки гипотезы для среднего значения. Однако формула немного меняется в зависимости от того, известна дисперсия или нет, поэтому мы сначала посмотрим, как это делается, когда дисперсия известна, а затем, когда дисперсия неизвестна.

С известным отклонением

Формула проверки гипотезы для среднего значения с известной дисперсией :

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle \frac{\sigma}{\sqrt{n}}}$

Золото:

$Z$

— статистика проверки гипотезы для среднего значения.
$\overline{x}$

это образец означает.
$\mu$

— предложенное среднее значение.
$\sigma$

— стандартное отклонение генеральной совокупности.
$n$

это размер выборки.

После того, как статистика проверки гипотезы для среднего рассчитана, результат следует интерпретировать как отклонение или отклонение нулевой гипотезы:

Если проверка гипотезы о среднем является двусторонней, нулевая гипотеза отклоняется, если абсолютное значение статистики превышает критическое значение Z _α/2 .
Если проверка гипотезы для среднего значения соответствует правому хвосту, нулевая гипотеза отклоняется, если статистика превышает критическое значение Z _α .
Если проверка гипотезы для среднего значения соответствует левому хвосту, нулевая гипотеза отклоняется, если статистика меньше критического значения -Z _α .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

В этом случае критические значения получаются из таблицы стандартизированного нормального распределения .

С неизвестной дисперсией

Формула проверки гипотезы для среднего с неизвестной дисперсией :

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Золото:

$t$

— это статистика проверки гипотезы для среднего значения, которое определяется t-распределением Стьюдента .
$\overline{x}$

это образец означает.
$\mu$

— предложенное среднее значение.
$s$

— выборочное стандартное отклонение.
$n$

это размер выборки.

Как и раньше, вычисленный результат тестовой статистики необходимо интерпретировать с критическим значением, чтобы отвергнуть или не отвергнуть нулевую гипотезу:

Если проверка гипотезы о среднем является двусторонней, нулевая гипотеза отклоняется, если абсолютное значение статистики больше критического значения t _α/2|n-1 .
Если проверка гипотезы для среднего значения соответствует правому хвосту, нулевая гипотеза отклоняется, если статистика больше критического значения t _α|n-1 .
Если проверка гипотезы для среднего значения соответствует левому хвосту, нулевая гипотеза отклоняется, если статистика меньше критического значения -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Когда дисперсия неизвестна, критические значения теста получают из таблицы распределения Стьюдента.

Реальный пример проверки гипотезы на среднее значение

Чтобы полностью понять концепцию проверки гипотез для среднего значения совокупности, вы можете увидеть реальный пример этого типа проверки гипотез ниже.

Технологическая компания утверждает, что батарея продаваемого ею ноутбука работает до 6 часов. Мы проверяем, является ли эта гипотеза ложной, выполняя проверку гипотезы с уровнем значимости α = 0,05. Для этого решено закупить 20 единиц и наблюдать за временем автономной работы каждого компьютера (значения выражаются в часах):

5,2 5,9 7,1 4,2 6,5
8,5 4,6 6,8 6,9 5,8
5,1 6,5 7,0 5,3 6,2
5,7 6,6 7,5 5,1 6,1

В этом случае нулевая и альтернативная гипотезы проверки гипотезы о среднем таковы:

$\begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}$

Чтобы определить статистику теста, нам сначала нужно вычислить среднее значение выборки и стандартное отклонение выборки:

$\overline{x}=6,13 \qquad s=1,05$

Поскольку мы не знаем дисперсию совокупности, чтобы получить тестовую статистику, нам нужно применить формулу проверки гипотезы для среднего значения с неизвестной дисперсией:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

$\displaystyle t=\frac{6,13-6}{\displaystyle \frac{1,05}{\sqrt{20}}}$

$\displaystyle t=0,68$

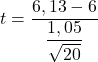
Теперь нам нужно найти критическое значение проверки гипотезы, поэтому мы ищем соответствующее значение в таблице распределения Стьюдента . Степени свободы t Стьюдента на единицу меньше размера выборки (20-1=19) и, с другой стороны, соответствующая вероятность составляет половину уровня значимости (0,05/2=0,025), поскольку это двусторонняя проверка гипотезы.

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}$

В заключение, поскольку это двусторонняя проверка гипотезы и абсолютное значение проверочной статистики меньше критического значения, нулевая гипотеза не отклоняется, а отклоняется альтернативная гипотеза.

$0,68<2,093 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

Проверка гипотез на разницу в средних значениях

Проверка гипотезы о разнице средних значений используется для отклонения или принятия нулевой гипотезы о том, что средние значения двух популяций одинаковы.

Таким образом, нулевая гипотеза проверки гипотезы о разнице двух средних всегда следующая:

$H_0: \mu_1=\mu_2$

Альтернативной гипотезой может быть одна из трех:

$\begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}$

Затем формула для расчета статистики проверки гипотезы для разницы средних значений, когда дисперсия известна :

$\displaystyle Z=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

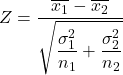
Золото:

$Z$

— это статистика проверки гипотезы для разницы двух средних значений с известной дисперсией, которая соответствует стандартному нормальному распределению.
$\overline{x_1}$

является средним значением образца 1.
$\overline{x_2}$

является средним значением образца 2.
$\sigma_1^2$

это дисперсия популяции 1.
$\sigma_2^2$

это дисперсия генеральной совокупности 2.
$n_1$

размер выборки 1.
$n_2$

размер выборки 2.

С другой стороны, формула для расчета статистики проверки гипотезы для разницы средних, когда дисперсия неизвестна, выглядит следующим образом:

$\displaystyle t=\frac{\displaystyle \overline{x_1}-\overline{x_2}}{\displaystyle\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

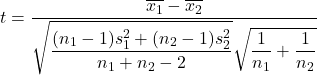
Золото:

$t$

— это статистика проверки гипотезы для разницы двух средних значений с неизвестной дисперсией, которая соответствует t-распределению Стьюдента.
$\overline{x_1}$

является средним значением образца 1.
$\overline{x_2}$

является средним значением образца 2.
$s_1^2$

– это дисперсия выборки 1.
$s_2^2$

– это дисперсия выборки 2.
$n_1$

размер выборки 1.
$n_2$

размер выборки 2.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Что такое проверка гипотезы на среднее значение?

Формула проверки гипотезы для среднего значения

С известным отклонением

С неизвестной дисперсией

Реальный пример проверки гипотезы на среднее значение

Проверка гипотез на разницу в средних значениях

Об авторе

бенджамин андерсон

Добавить комментарий