Простая линейная регрессия

К бенджамин андерсон 2 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое простая линейная регрессия в статистике и как она выполняется. Аналогично, вы найдете решение простого упражнения по линейной регрессии и, кроме того, простой калькулятор линейной регрессии в Интернете.

Что такое простая линейная регрессия?

Простая линейная регрессия — это статистическая модель, используемая для связи независимой переменной, и мы пытаемся аппроксимировать связь между двумя переменными.

Поэтому простая линейная регрессия используется для нахождения уравнения, которое линейно связывает две переменные. Логично, что связь между двумя переменными должна быть линейной, в противном случае необходимо использовать другой тип модели регрессии.

Уравнение простой модели линейной регрессии состоит из двух коэффициентов: константы уравнения (b ₀ ) и коэффициента корреляции между двумя переменными (b ₁ ). Следовательно, уравнение простой модели линейной регрессии имеет вид y=b ₀ +b ₁ x.

$y=b_0+b_1x$

Уравнение простой линейной регрессии изображается в виде прямой линии, поэтому коэффициент b ₀ представляет собой точку пересечения, а коэффициент b ₁ представляет собой наклон линии.

Простые формулы линейной регрессии

Формулы расчета коэффициентов простой линейной регрессии следующие:

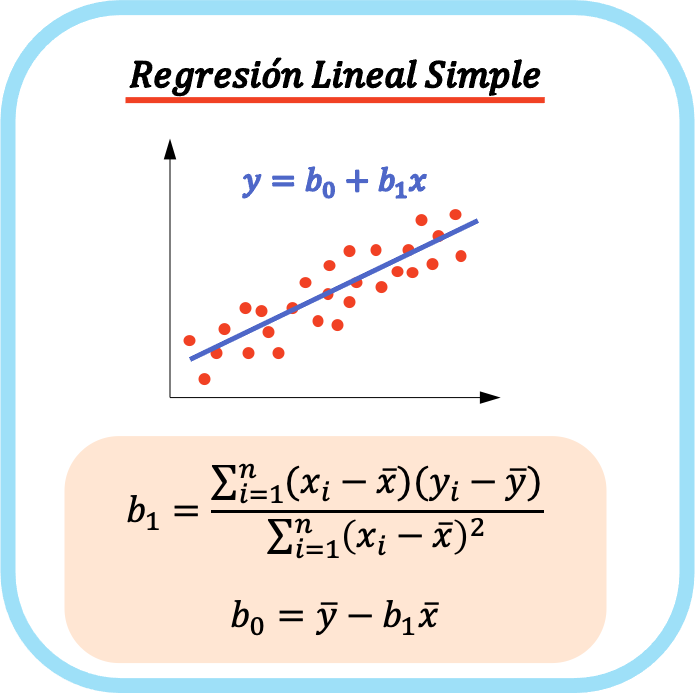
👉 Вы можете использовать калькулятор ниже, чтобы рассчитать коэффициенты простой линейной регрессии для любого набора данных.

Очевидно, что уравнение, полученное на основе простой модели линейной регрессии, не сможет угадать точное значение всех наблюдений, поскольку эта модель просто пытается найти уравнение, которое аппроксимирует связь между двумя переменными. Таким образом, остаток определяется как разница между истинным значением и значением, оцененным с помощью модели линейной регрессии.

$e_i=y_i-\widehat{y}_i$

Обратите внимание, что цель модели простой линейной регрессии — минимизировать квадраты остатков, то есть простая линейная регрессия основана на критерии наименьших квадратов .

Конкретный пример простой линейной регрессии

Чтобы завершить понимание метода простой линейной регрессии, приведем практический пошаговый пример, в котором уравнение модели простой линейной регрессии рассчитывается на основе набора статистических данных.

После сдачи экзамена по статистике пятерым студентам был задан вопрос, сколько часов обучения они посвятили экзамену. Данные представлены в таблице ниже. Выполните простую модель линейной регрессии собранных статистических данных, чтобы линейно связать учебные часы с достигнутой оценкой.

Чтобы реализовать простую модель линейной регрессии, мы должны определить коэффициенты b ₀ и b ₁ уравнения, и для этого мы должны использовать формулы, представленные в разделе выше.

Однако, чтобы применить простые формулы линейной регрессии, мы должны сначала вычислить среднее значение независимой переменной и среднее значение зависимой переменной:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Теперь, когда мы знаем средние значения переменных, мы вычисляем коэффициент b ₁ модели, используя соответствующую формулу:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Наконец, мы вычисляем коэффициент b ₀ модели, используя соответствующую формулу:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

Короче говоря, уравнение простой модели линейной регрессии проблемы:

$y=2,0294+0,4412x$

Ниже вы можете увидеть графическое представление выборочных данных, а также прямую линию простой модели линейной регрессии:

Наконец, после того как мы рассчитали уравнение простой модели линейной регрессии, остается только интерпретировать полученный результат. Для этого необходимо рассчитать коэффициент детерминации регрессионной модели, посмотреть, как это делается, можно, выполнив поиск соответствующей статьи на нашем сайте.

Простые предположения линейной регрессии

Чтобы выполнить простую линейную регрессию, должны быть выполнены следующие предположения:

Независимость : наблюдаемые остатки должны быть независимы друг от друга. Распространенный способ обеспечить независимость модели — добавить случайность в процесс выборки.
Гомоскедастичность : дисперсии остатков должны быть однородными, то есть изменчивость остатков должна быть постоянной.
Нормальность : остатки должны быть нормально распределены или, другими словами, они должны следовать нормальному распределению со средним значением 0.
Линейность . Связь между независимой переменной и зависимой переменной должна быть линейной.

Простой калькулятор линейной регрессии

Вставьте образец данных в калькулятор ниже, чтобы создать простую модель линейной регрессии между двумя переменными. Вам необходимо разделить пары данных так, чтобы в первом поле были только значения независимой переменной X, а во втором поле — только значения зависимой переменной Y.

Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Простая и множественная линейная регрессия

Наконец, мы увидим, в чем разница между простой линейной регрессией и множественной линейной регрессией, поскольку это два типа линейных регрессий, часто используемых в статистике.

Множественная линейная регрессия позволяет математически связать две или более объясняющие переменные с переменной отклика. То есть при множественной линейной регрессии создается модель, в которой есть как минимум две независимые переменные.

Следовательно, разница между простой линейной регрессией и множественной линейной регрессией заключается в количестве независимых переменных. В простой линейной регрессии существует только одна независимая переменная, тогда как в множественной линейной регрессии есть две или более независимых переменных.

➤ См.: Множественная линейная регрессия.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше