Как выполнить простую линейную регрессию в sas

Простая линейная регрессия — это метод, который мы можем использовать, чтобы понять взаимосвязь между переменной-предиктором и переменной отклика .

Этот метод находит строку, которая лучше всего «соответствует» данным, и принимает следующую форму:

ŷ = б ₀ + б ₁ х

Золото:

• ŷ : Предполагаемое значение ответа.
• b ₀ : Начало линии регрессии.
• b ₁ : Наклон линии регрессии.

Это уравнение помогает нам понять взаимосвязь между переменной-предиктором и переменной отклика.

В следующем пошаговом примере показано, как выполнить простую линейную регрессию в SAS.

Шаг 1. Создайте данные

В этом примере мы создадим набор данных, содержащий общее количество изученных часов и оценку итогового экзамена 15 студентов.

Мы подберем простую модель линейной регрессии, используя часы в качестве предикторной переменной и оценку в качестве переменной отклика.

Следующий код показывает, как создать этот набор данных в SAS:

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

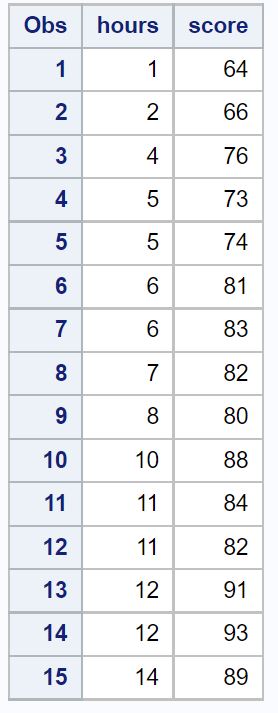
Шаг 2. Подберите простую модель линейной регрессии.

Далее мы будем использовать proc reg для соответствия простой модели линейной регрессии:

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

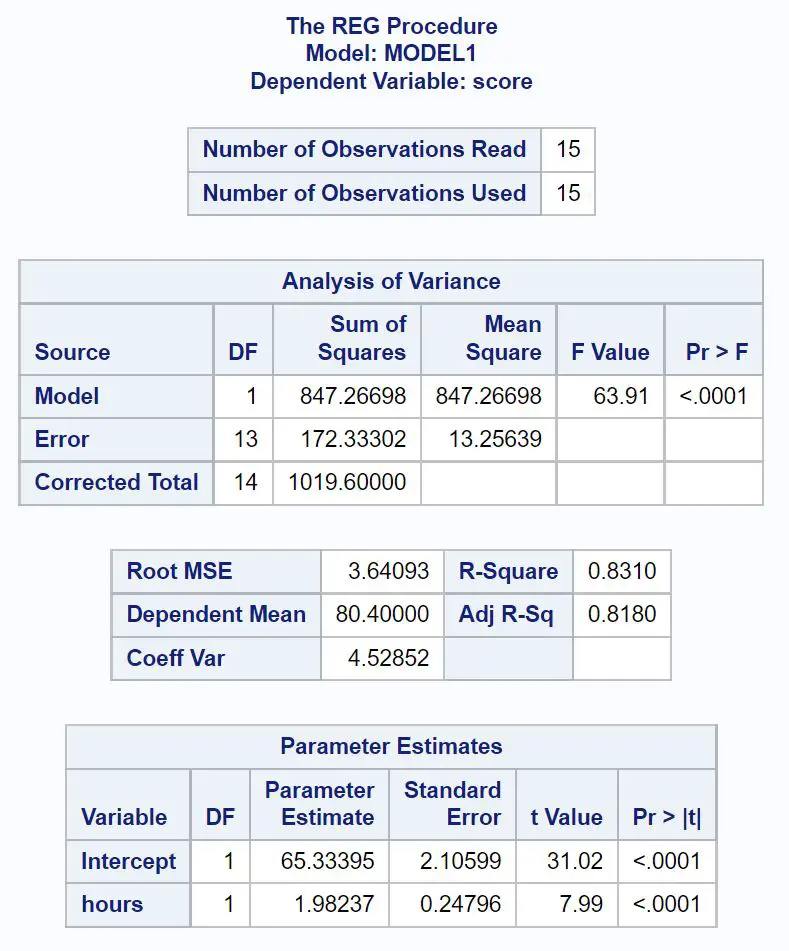
Вот как интерпретировать наиболее важные значения из каждой таблицы в результате:

Таблица анализа пробелов:

Общее значение F регрессионной модели составляет 63,91 , а соответствующее значение p составляет <0,0001 .

Поскольку это значение p меньше 0,05, мы заключаем, что регрессионная модель в целом статистически значима. Другими словами, часы — полезная переменная для прогнозирования результатов экзамена.

Таблица соответствия модели:

Значение R-квадрата показывает процент вариации результатов экзамена, который можно объяснить количеством учебных часов.

В общем, чем больше значение R-квадрата регрессионной модели, тем лучше переменные-предикторы прогнозируют значение переменной отклика.

В этом случае 83,1% разброса результатов экзамена можно объяснить количеством изученных часов. Это значение довольно велико, что указывает на то, что количество учебных часов является очень полезной переменной для прогнозирования результатов экзамена.

Таблица оценок параметров:

Из этой таблицы мы можем увидеть подобранное уравнение регрессии:

Оценка = 65,33 + 1,98*(часы)

Мы интерпретируем это так, что каждый дополнительный час обучения связан со средним увеличением экзаменационной оценки на 1,98 балла .

Исходное значение говорит нам, что средний балл на экзамене для студента, обучающегося ноль часов, составляет 65,33 .

Мы также можем использовать это уравнение, чтобы найти ожидаемый результат экзамена на основе количества часов обучения студента.

Например, студент, который учится 10 часов, должен набрать на экзамене балл 85,13 :

Оценка = 65,33 + 1,98*(10) = 85,13

Поскольку значение p (<0,0001) для часов в этой таблице меньше 0,05, мы делаем вывод, что это статистически значимая предикторная переменная.

Шаг 3. Анализ остаточных графиков

Простая линейная регрессия делает два важных предположения относительно остатков модели:

• Остатки распределены нормально.
• Остатки имеют одинаковую дисперсию (« гомоскедастичность ») на каждом уровне переменной-предиктора.

Если эти предположения не выполняются, то результаты нашей регрессионной модели могут быть ненадежными.

Чтобы убедиться, что эти предположения выполняются, мы можем проанализировать остаточные графики, которые SAS автоматически отображает в выходных данных:

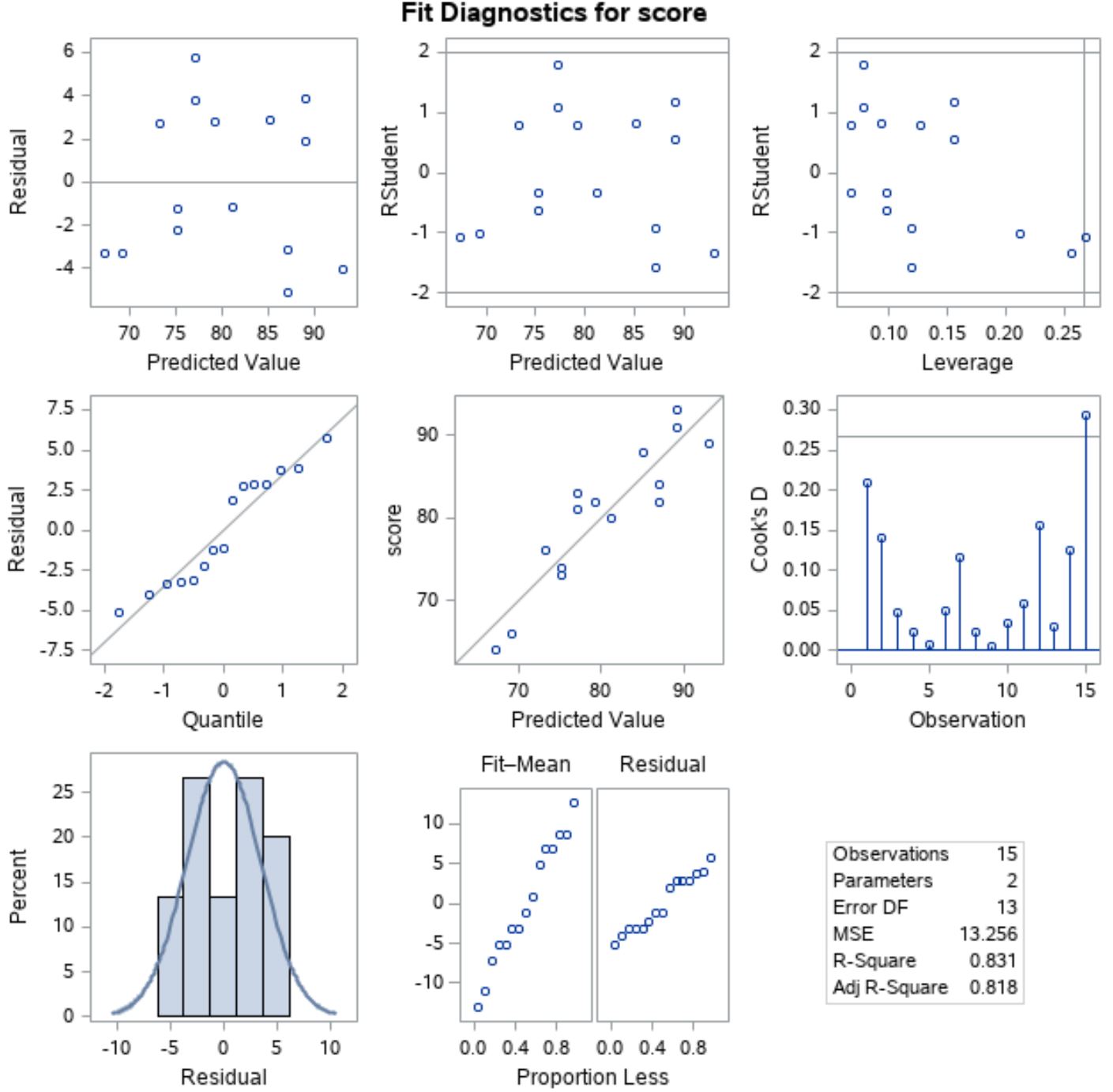
Чтобы убедиться, что остатки распределены нормально , мы можем проанализировать график в левом положении средней линии с «Квантилем» по оси X и «Остатком» по оси Y.

Этот график называется графиком QQ , сокращенно от «квантиль-квантиль», и используется для определения нормального распределения данных или нет. Если данные распределены нормально, точки на графике QQ будут лежать на прямой диагональной линии.

На графике видно, что точки лежат примерно вдоль прямой диагональной линии, поэтому можно предположить, что остатки распределены нормально.

Затем, чтобы убедиться, что остатки гомоскедастичны , мы можем посмотреть на график в левой позиции первой строки с «Прогнозируемым значением» по оси X и «Невязкой» по оси Y.

Если точки графика случайно разбросаны вокруг нуля без четкой закономерности, то можно предположить, что остатки гомоскедастичны.

Из графика мы видим, что точки разбросаны вокруг нуля случайным образом с примерно одинаковой дисперсией на каждом уровне по всему графику, поэтому мы можем предположить, что остатки гомоскедастичны.

Поскольку оба предположения выполняются, мы можем предположить, что результаты простой модели линейной регрессии надежны.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в SAS:

Как выполнить односторонний дисперсионный анализ в SAS
Как выполнить двусторонний дисперсионный анализ в SAS
Как рассчитать корреляцию в SAS