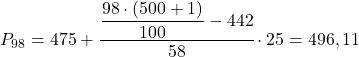Процентили (статистика)
В этой статье объясняется, что такое процентиль и как он рассчитывается. Вы найдете решенные упражнения с процентилями и, кроме того, сможете вычислить любой процентиль вашей выборки данных с помощью онлайн-калькулятора.
Что такое процентили?
В статистике процентили — это значения, делящие набор упорядоченных данных на сто равных частей. Итак, процентиль указывает значение, ниже которого падает процент набора данных.
Например, значение 35-го процентиля выше, чем у 35% наблюдаемых данных, но ниже, чем у остальных данных.
Процентили обозначаются заглавной буквой P и индексом процентиля, то есть 1-й процентиль — P 1 , 40-й процентиль — P 40 , 79-й процентиль — P 79 и так далее.

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать процентили любого набора данных.
Точно так же процентили являются мерой нецентрального положения наряду с квартилями, квинтилями и децилями. Вы можете проверить значение каждого из этих типов квантилей на нашем сайте.
Следует отметить, что термин процентили также используется для сравнения веса и роста ребенка со стандартными значениями других малышей, поскольку существуют таблицы роста с записанными значениями, которые помогают определить, правильно ли растет ребенок или нет. . .
Как посчитать процентили
Чтобы вычислить положение процентиля ряда статистических данных, необходимо умножить число процентилей на сумму общего количества точек данных плюс один и разделить результат на сто.
Таким образом, формула процентиля выглядит следующим образом:
![]()
Обратите внимание: эта формула сообщает нам положение процентиля, но не его значение. Процентилем будут данные, расположенные в позиции, полученной по формуле.
Однако иногда результат этой формулы дает нам десятичное число, поэтому мы должны различать два случая в зависимости от того, является ли результат десятичным числом или нет:
- Если результатом формулы является число без десятичной части , процентиль соответствует данным, которые находятся в позиции, указанной формулой выше.
- Если результатом формулы является число с десятичной частью , точное значение процентиля рассчитывается по следующей формуле:
![]()
Где x i и x i+1 — номера позиций, между которыми находится число, полученное по первой формуле, а d — десятичная часть числа, полученного по первой формуле.
Теперь вы можете подумать, что найти процентили статистической выборки или совокупности сложно, поскольку метод включает в себя множество шагов, но на самом деле это просто. Прочтите следующие два конкретных примера, и я уверен, вы поймете это намного лучше.
Примечание . Научное сообщество еще не пришло к единому мнению о том, как рассчитывать процентили, поэтому вы можете найти книгу по статистике, в которой это объясняется немного по-другому.
Примеры расчета процентилей
Как вы видели выше в объяснении того, как найти процентили выборки, расчет варьируется в зависимости от того, является ли результат первой формулы десятичным или нет. Поэтому ниже вы найдете два решенных примера, по одному на каждый случай.
Пример 1
- По данным, приведенным в следующей таблице, рассчитайте 1-й, 43-й и 89-й процентили.
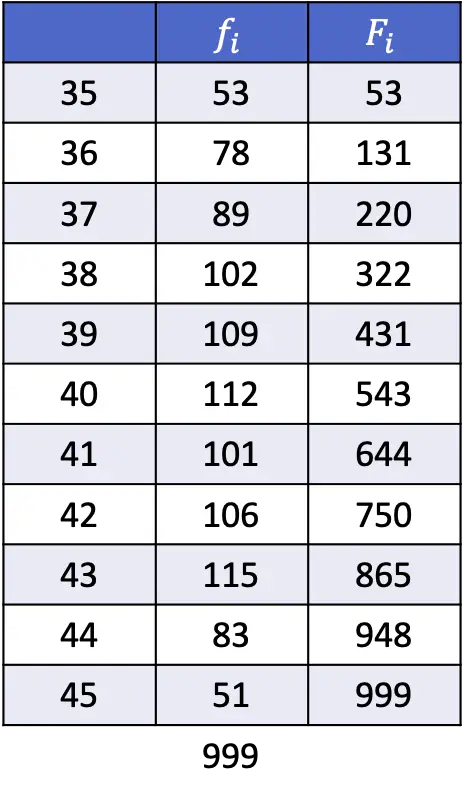
Как объяснялось в предыдущем разделе, формула для определения положения процентиля выглядит следующим образом:
![]()
В этом случае размер выборки для этого упражнения составляет 999 статистических данных, поэтому для расчета положения первого процентиля нам нужно заменить 999 на n и 1 на k :
![]()
Таким образом, 1-й процентиль будет тем, чья совокупная абсолютная частота сразу превышает 10, что в данном случае равно 35, поскольку его совокупная абсолютная частота равна 53.
Чтобы определить 43-й процентиль, вы должны использовать ту же формулу, но, очевидно, на этот раз мы заменим k на 43.
![]()
Абсолютная совокупная частота непосредственно выше 430 равна 431 из данных 39, поэтому 43-й процентиль равен 39.
Наконец, мы применяем ту же формулу для получения 89-го процентиля:
![]()
Совокупная абсолютная частота значения 44 равна 948, что сразу больше, чем 890. Следовательно, 89-й процентиль равен 44.
Пример 2
- Найдите 35-й и 67-й процентили следующего ряда данных:
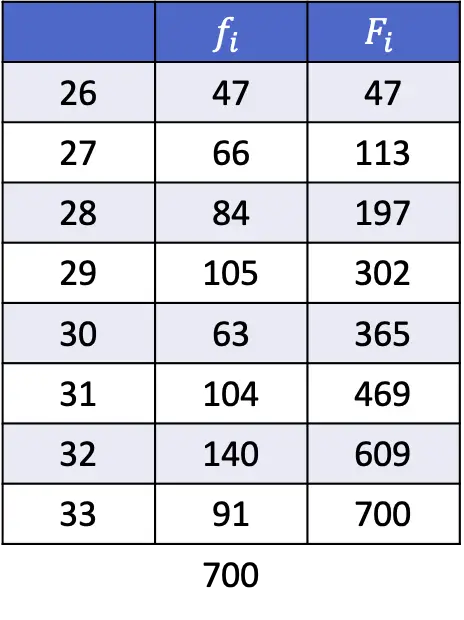
Даже если в этом упражнении нам придется выполнить больше вычислений, принцип все тот же: мы должны вычислить положение процентиля с помощью следующего выражения.
![]()
Таким образом, для расчета 35-го процентиля мы заменяем k на 35, а n на общее количество данных, т. е. 700:
![]()
Но на этот раз мы получили из формулы десятичное число, поэтому нам нужно применить следующее алгебраическое выражение для расчета точного значения процентиля:
![]()
Число, заданное первой формулой, равно 245,35, поэтому 35-й процентиль находится между позициями 245 и 246, что соответствует значениям 29 и 29 соответственно. Следовательно, x i равно 29, x i+1 равно 29, а d равно десятичной части полученного числа, т. е. 0,35.
![]()
Чтобы найти 67-й процентиль, нам нужно использовать тот же метод. Сначала мы вычисляем процентильную позицию:
![]()
Полученное число 469,67 указывает на то, что процентиль будет находиться между позициями 469 и 470, значения которых равны 31 и 32. Поэтому в процессе работы мы используем вторую формулу, чтобы найти точное значение процентиля:
![]()
процентиль калькулятор
Введите набор статистических данных и процентиль, который вы хотите рассчитать, в следующий калькулятор. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.
Процентили в сгруппированных данных
Чтобы рассчитать процентили, когда данные сгруппированы в группы , нам сначала нужно найти группу или класс, к которому относится процентиль, используя следующую формулу:
![]()
Таким образом, процентиль будет находиться в интервале, абсолютная частота которого сразу больше числа, полученного в предыдущем выражении.
И как только мы уже знаем интервал, к которому принадлежит процентиль, мы должны применить следующую формулу, чтобы найти точное значение процентиля:
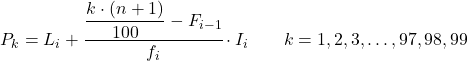
Золото:
- Li — нижняя граница интервала, в котором лежит процентиль.
- n — общее количество наблюдений.
- F i-1 представляет собой совокупную абсолютную частоту предыдущего интервала.
- f i — абсолютная частота интервала, в котором лежит процентиль.
- I i — ширина процентильного интервала.
Ниже приведено пошаговое упражнение по получению процентилей, когда данные выражены в интервалах. В частности, рассчитываются 29-й, 52-й и 98-й процентили.

Данные в этой выборке сгруппированы как интервалы, поэтому для определения процентилей нам нужно выполнить два шага: сначала нам нужно найти интервал, в который попадает процентиль, а затем применить формулу для расчета точного значения процентиля. процентиль.
Таким образом, мы находим положение 29-го процентиля с помощью следующего выражения:
![]()
![]()
Процентильным интервалом будет тот, чья совокупная абсолютная частота сразу превышает 145,29, что в данном случае представляет собой интервал [350,375), чья совокупная абсолютная частота равна 175. И как только мы узнаем процентильный интервал, мы применим следующую формулу для его расчета. точное значение:
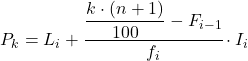
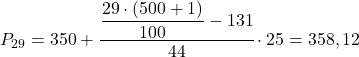
Теперь мы повторяем ту же процедуру для расчета 52-го процентиля. Сначала вычислим его интервал:
![]()
Интервал 52-го процентиля равен [400,425), поскольку его совокупная абсолютная частота (298) находится непосредственно над 260,52. Таким образом, точное значение процентиля будет:
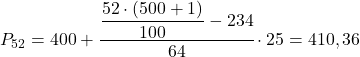
Наконец, мы найдем 98-й процентиль. Как всегда, сначала вычисляем интервал, в котором он лежит:
![]()
И как только мы узнаем интервал, в котором находится процентиль, мы рассчитаем его точное значение по следующей формуле: